First Law of Thermodynamics Application to closed systems (Non-Flow Processes)

 The processes occurring in closed systems which do not permit the transfer of mass across their boundaries are known as non-flow processes.

FIRST LAW OF THERMODYNAMICS APPLICATION TO CLOSED SYSTEMS (NON-FLOW PROCESSES)

The processes occurring in closed systems which do not permit the transfer of mass across their boundaries are known as non-flow processes. In non-flow processes, there are only heat transfer and work transfer but there is no mass transfer into or out of the system.

During the energy flow, the changes take place in pressure, volume, temperature, internal energy, heat, work, etc.

A gas may be heated or cooled and expanded or compressed by different methods. According to the above-said statement, there are different processes as given below:

(a) Constant volume or Iso-choric process 

(b) Constant pressure or Iso-baric process.

(c) Constant temperature or Isothermal process

(d) Hyperbolic process

(e) Reversible adiabatic or Isentropic process

(f) Polytropic process

(g) Free expansion process

(h) Throttling process.

Before discussing the various processes, some important terms related to these processes should be familiar for better understanding.

Work (W):

For any non-flow process, the mechanical work is mathematically given by

where

p = Pressure in N/m2

V = Volume in m3

Note:

Area under p-V diagram represents the work done during the process and the area under T-s diagram represents heat transfer during the process.

Internal energy (U):

Internal energy is defined as the heat energy stored in the gas at a given temperature. Mathematically, it can be expressed by

ΔU = m Cv ΔT   ….. (1.49)

where

m = Mass of the system in kg

Cv = Specific heat capacity at constant volume in kJ/kgK

T = Temperature of the gas (K)

The increase of heat energy stored in the gas due to raise in temperature is known as change in internal energy.

Mathematically, the change in internal energy can be written as

ΔU = m Cv (T2 - T1)    …(1.50)

where

T2 = Final temperature after heating

T1 = Initial temperature before heating.

Enthalpy (H):

Enthalpy is defined as the total heat of the substance. It is equal to the sum of internal energy (U) and pressure volume product (i.e. pV).

Enthalpy, H = U + pV

For unit mass, it can be written as

Specific enthalpy, h = u + pv

Enthalpy is also a function of temperature. Mathematically, it is given by

Enthalpy, H = mCp T

Change in enthalpy, ΔH = ΔU + pΔV    ... (1.51)

Change in enthalpy, ΔH = m Cp ΔT    ... (1.52)

1. Constant Volume (or) Iso-Choric Process

When a gas is heated at constant volume (i.e. fixed space), its temperature and pressure will increase. It is called constant volume process. Since the gas is heated in the fixed space, no work is done by the system. The entire heat energy supplied to the gas is stored in the gas itself as internal energy.

The gas is heated from state 1 to 2 as shown in Figure 1.37.

In Figure 1.37,

p1 and p2 = Pressures at initial and final states 

T1 and T2 = Temperatures at initial and final states

V1 and V2 = Volumes at initial and final states.

In constant volume process, there is no area under p-V diagram. Therefore, there is no work done during the process.

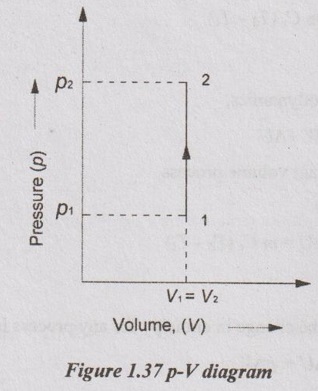
Relation between p, V and T:

From characteristic gas equation,

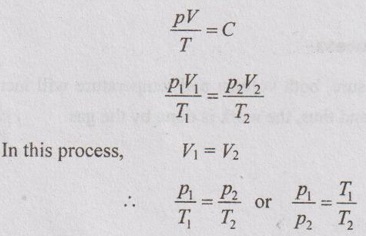
Work done (W):

Work done during any process is given by

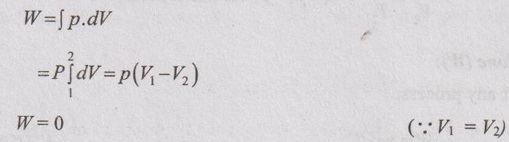
Change in internal energy (ΔU):

From equation (1.49), the change in internal energy for any process is given by

ΔU = m Cv dT

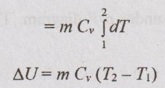
Heat transfer (Q):

From first law of thermodynamics,

Q = W + ΔU

We know that for constant volume process,

W = 0

Q = ΔU = m Cv (T2 - T1)

Change in enthalpy (ΔH):

From equation (1.51), the change in enthalpy for any process is given by

ΔH = ΔU + pΔV

In this process, V1 = V2 and hence ΔV = 0

⸫ ΔH = ΔU = m Cv (T2 - T1)

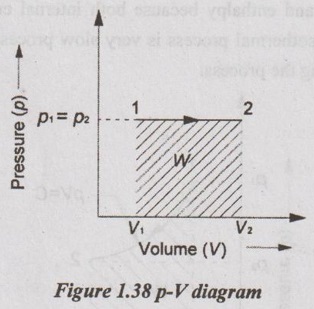
2. Constant Pressure or Isobaric Process

When a gas is heated at constant pressure, both volume and temperature will increase. The gas expands in the cylinder by heating and thus, the work is done by the gas.

Relation between p, V and T:

From characteristic gas equation

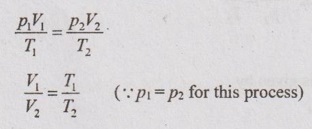
Work done (W):

For any process,

W = p (V2 - V1)

W = p2V2 - p1V1 = m R (T2 - T1)

Area under the curve in p-V diagram represents the work done during the process.

Change in internal energy (ΔU):

For any process,

ΔU = m Cv dT

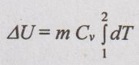
ΔU = m Cv (T2 - T1)

Heat transferred (Q):

Q = W + ΔU = p (V2 - V1) + m Cv (T2 - T1)

Q = m R(T2 - T1) + m Cv (T2 - T1)

Q = m (Cp - Cv)( T2 - T1) + m Cv (T2 - T1)   (⸪  R = Cp - Cv) 

Q = m Cp (T2 - T1)

Change in enthalpy (ΔH):

ΔH = m Cp dT

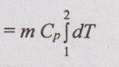
ΔH = m Cp (T2 - T1)

3. Constant Temperature or Iso-Thermal Process

In this process, the temperature of the working substance remains constant, the pressure decreases and the volume increases. Hence, there is no change in temperature, there is no change in internal energy and enthalpy because both internal energy and enthalpy are the functions of temperature. Isothermal process is very slow process so that the temperature is constantly maintained during the process.

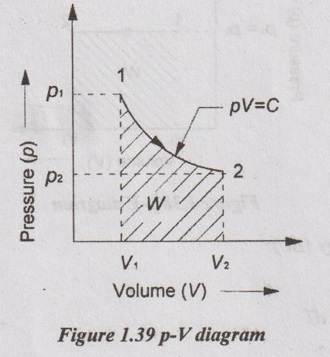
Relation between p, V and T:

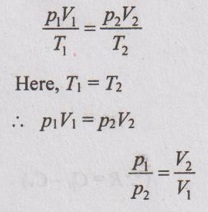
Work done (W):

For any process

The characteristic gas equation is given by

PV / T = C 

Here, T = constant

pV = constant

pV = C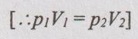

p = C/V

Substituting the value of p in equation (1.53),

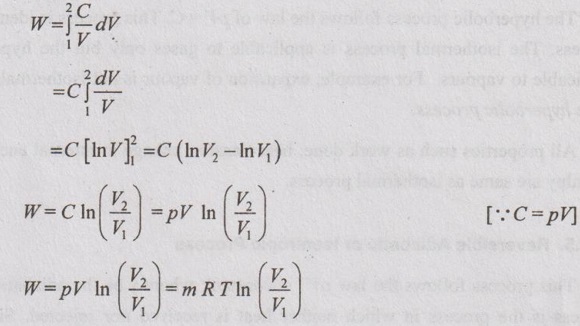
Change in internal energy (ΔU):

ΔU = m Cv dT = m Cv (T2 - T1)

Since T2 = T1

ΔU = 0

There is no change in internal energy.

Heat transferred (Q):

From first law of thermodynamics,

Q = W + ΔU

In this process, ΔU = 0

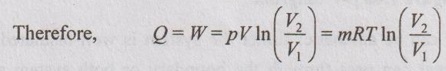
Change in enthalpy (ΔH):

ΔH = m Cp dT

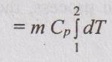
Since, dT = 0

⸫  ΔH = 0

There is no change in enthalpy.

4. Hyperbolic Process

The hyperbolic process follows the law of pV= C. This process is identical to isothermal process. The isothermal process is applicable to gases only but the hyperbolic process is applicable to vapours. For example, expansion of vapour is not isothermal process, it is said to be hyperbolic process.

All properties such as work done, heat transfer, change in internal energy and change in enthalpy are same as isothermal process.

5. Reversible Adiabatic or Isentropic Process

This process follows the law pVγ = constant; where γ be the adiabatic index. Adiabatic process is the process in which neither heat is received nor rejected. Simply, there is no transfer of heat during the process.

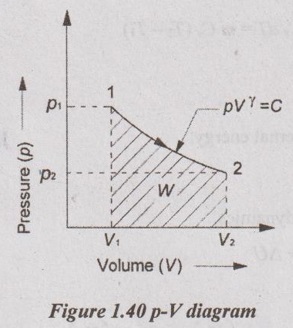
There are two ways a process can be adiabatic: Either the system is well-insulated so that only a negligible amount of heat can pass through the boundary or both system and surroundings are at the same temperature and therefore, there is no temperature difference for the heat transfer. An adiabatic process should not be confused with an isothermal process. Even though there is no heat transfer during an adiabatic process, the energy content and temperature of a system can still be changed by other means such as work. Adiabatic process is a very rapid process so that there is no heat transfer during the process.

Relationship between p, V and T:

From adiabatic equation, pVγ = C

p1V1γ = p2V2γ

The relationship between p and V,

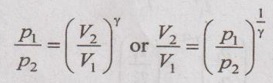
The relation between temperature and volume can be written as

Applying the above equation to initial and final states,

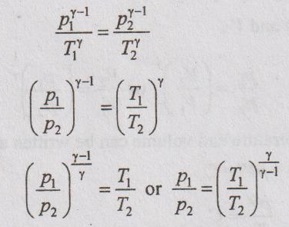
For the sake of simplicity to solve problems, it can be written as

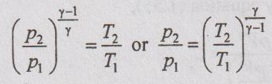
Work done (W):

Heat transfer (Q):

There is no heat transfer during adiabatic process,

⸫ Q = 0

Change in internal energy (ΔU):

From first law of thermodynamics,

Q = W + ΔU

In this process, Q = 0

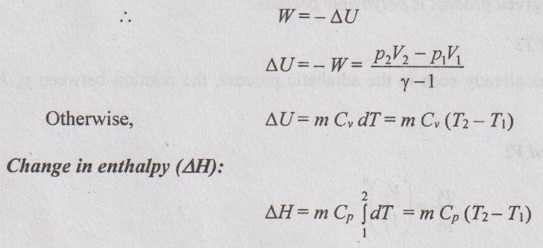
6. Polytropic Process

This process follows the law pVn = constant; where n be the polytropic index. It is also called a general law of expansion and compression of gases.

The polytropic index 'n' has any value from zero to infinity which is depending upon the process. The various values of index 'n' and their processes are given below.

(a) When n = 0

pVn = C; apply n = 0

pV° = 0 or p = C

It is called constant pressure or isobaric process.

(b) When n = 1

pV1= C i.e., pV = C

It shows that the process is constant temperature or isothermal process.

(c) When n = ∞

V∞ = C or V = C

It shows that the process is constant volume process or isochoric process.

(d) When n = γ

pVγ = C

It shows that the process is reversible adiabatic or isentropic process.

(e) When n = n

pVn = C

It shows that the given process is polytropic process.

Relation between p, V and T:

In a similar manner as already seen in the adiabatic process, the relation between p, V and T can be derived.

(a) Relation between p and V:

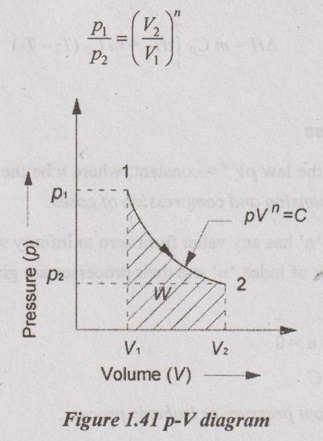
(b) Relation between T and V:

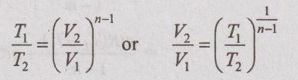
(c) Relation between T and p:

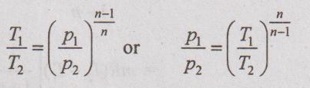
(d) Value of 'n':

From polytropic equation,

p1V1n = p2V2n

Taking logarithms on both sides,

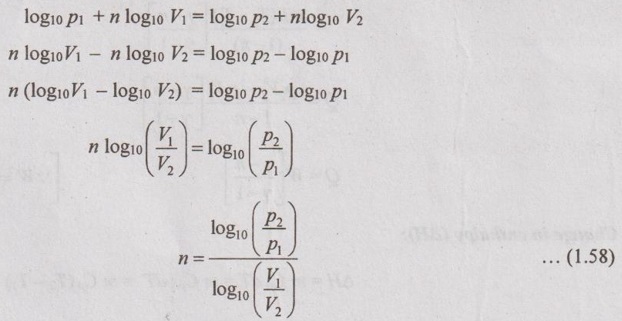
Work done (W):

Work done is also derived similar to adiabatic process. Instead of 'γ', substituting 'n'.

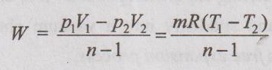
Change in internal energy (ΔU):

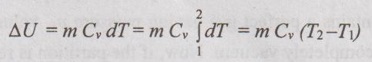
Heat transfer (Q):

From first law, Q = W + ΔU

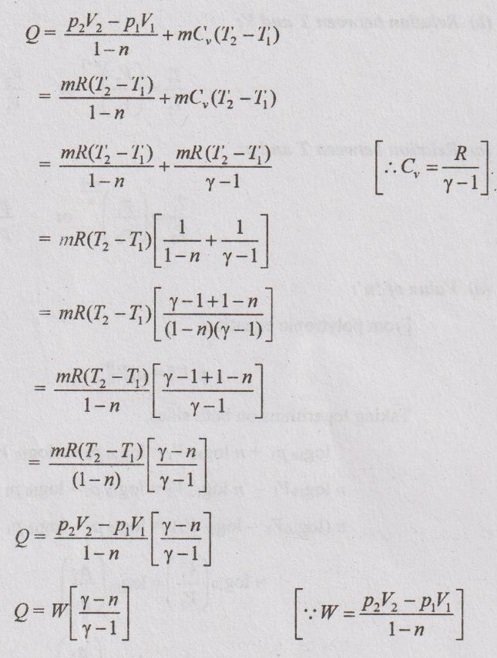
Change in enthalpy (ΔH):

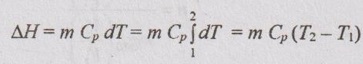
7. Free Expansion Process

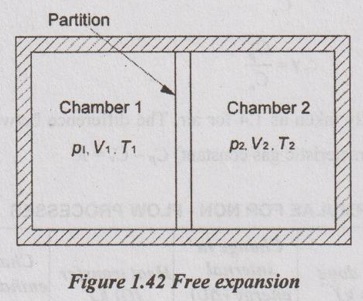
It is also called unresisting expansion process. It is one of the irreversible processes. If a fluid is allowed to expand suddenly into a vacuum chamber through an orifice of large dimension, it is known as free expansion process.

Consider two chambers 1 and 2 separated by a partition as shown Figure 1.42. Let, the chamber 1 contains a perfect gas having pressure p1, volume V1 and temperature T1 and the chamber 2 is completely vacuum. Now, if the partition is removed, the gas will expand freely and occupy the whole space. During this process, no work is done by the system (W = 0).

Both chamber 1 and chamber 2 are perfectly insulated. Therefore, no heat transfer takes place (Q = 0).

By first law, Q = W + ΔU

ΔU = 0 since Q = 0, W = 0.

There is no change in internal energy.

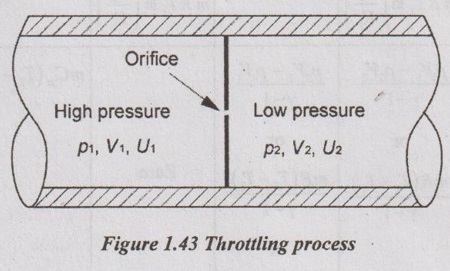
8. Throttling Process

When a fluid expands through a minute aperture orifice or slightly opened value, the process is called throttling process.

During the throttling process, both pressure and velocity are reduced. But there is no heat transfer and no work done by the system.

i.e. Q = 0 and W = 0

Hence, there is no change in internal energy (ΔU = 0)