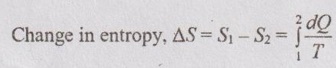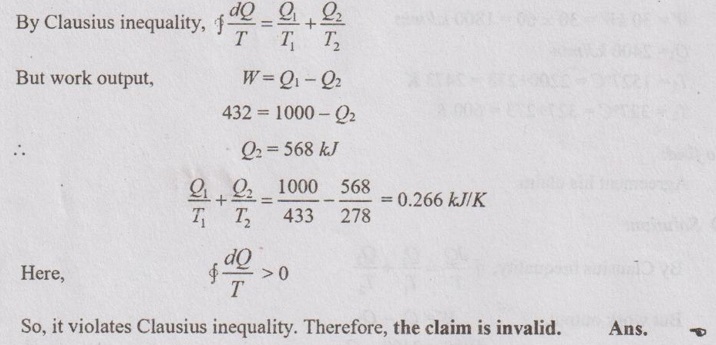Entropy change for a pure substance

 When the water is continuously heated, the temperature increases up to 100°C without changing its phase.

ENTROPY CHANGE FOR A PURE SUBSTANCE

(i) Compressed liquid:

When the water is continuously heated, the temperature increases up to 100°C without changing its phase. The heat contained in the water before reaching 100°C is only sensible heat. The sensible heat also contains entropy. It can be taken from compressed liquid tables for pure substance.

(ii) Saturated liquid:

The water at 100°C called saturated liquid has the highest sensible heat. The entropy of saturated water at this point is denoted with the subscription of 'f'. The specific entropy is sf. The steam is considered as a pure substance. The entropy of saturated liquid can be taken from steam tables for the particular pressure or temperature.

Specific entropy, sf is given in terms of kJ/kgK

(iii) Saturated mixture steam or wet steam:

At 100°C, the steam formation will start. During further heating of saturated water, the phase change takes place from liquid to gas called steam. It continues until the whole water is fully converted into steam. At the end of steam formation, the steam is in dry saturated condition. So, the saturated mixture steam at any point between saturated liquid region and dry saturated region is wet steam. It means, the steam in saturated mixture region will have the percentage of dryness fraction from 0 - 100%. Due to this reason, the factor dryness fraction comes into consideration to obtain the exact entropy at any point in the saturated mixture region.

If the dryness fraction is zero value, it is designated as saturated liquid by indicating the start point of the steam formation in the heating process.

If the dryness fraction is 100%, is designated as dry saturated steam by indicating the end point of the steam formation in the heating process.

The entropy of saturated steam is denoted with the subscription of 'fg'. The specific entropy is sfg. The entropy of saturated steam can be taken from saturated steam tables for the particular pressure or temperature.

Specific entropy, sfg is given in terms of kJ/kgK

The entropy can be calculated at any point in the saturated mixture region as follows:

Specific entropy, s = sf + x sfg

(iv) Dry saturated steam:

As per earlier discussions, the dry steam will have 100% dryness fraction. The entropy of dry saturated steam is denoted with the subscription of 'g'. The specific entropy is sg. The entropy of dry saturated steam can be taken from saturated steam tables for the particular pressure or temperature.

Specific entropy, sg is given in terms of kJ/kgK

(v) Superheated steam:

Due to further heating of dry steam, the temperature of dry steam gets increased. This steam is called superheated steam. It is mainly used in power plant cycles in order to increase the work output of the process. The entropy of superheated steam is denoted with the subscription of 'sup'. The specific entropy is ssup. The entropy of superheated steam can be taken from superheated entropy table for the particular pressure and temperature.

Specific entropy ssup is given in terms of kJ/kgK

If specific heat and degree of super heat of the superheated steam are known, the entropy can also be calculated by using the formulae below.

Specific entropy,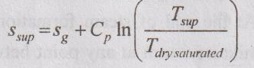

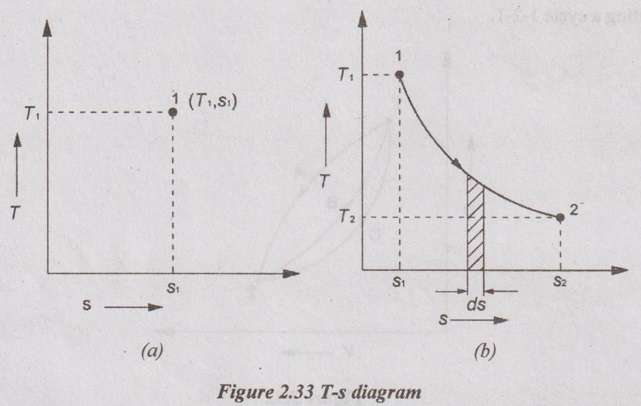
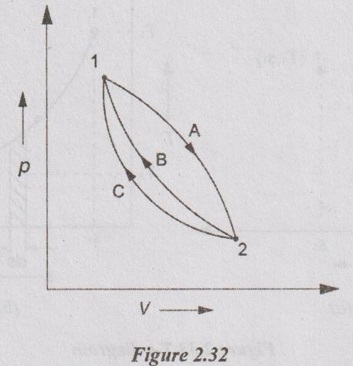
The change in entropy for the process from state 1 to state 2 is denoted by Δs. For example, the change in entropy of the process which has the start point in the saturated mixture region and end point in the superheated region. First, the entropy for state 1 and state 2 are calculated by following the above-mentioned procedure for each region. Then, the change in entropy is calculated by

Δs = s2 - s1 for unit mass of the system.

The detailed study on pure substances is made in Unit 4.

Tds Equations

 Based on the first law of thermodynamics, Heat transfer, Q = Work done (W) + Internal energy (ΔU) TdS = pdV + dU

Tds EQUATIONS

Based on the first law of thermodynamics,

Heat transfer, Q = Work done (W) + Internal energy (ΔU)

TdS = pdV + dU

It can be rewritten as

TdS = dU + pdV     ……(2.33)

For unit mass,

Tds = du + pdv        ….. (2.34)    

Equation (2.33) is the first Tds equation or Gibb's function.

We know that

Enthalpy, h = u + pv

Differentiating above enthalpy equation, it becomes

Enthalpy, dh = du + d(pv) = du + vdp + pdv

⸫ du = dh – vdp – pdv     ... (2.35)

Substituting equation (2.35) in (2.34),

Tds = dh – vdp - pdv + pdv

Tds = dh – vdp    ….(2.36)

Equation (2.36) is the second Tds equation.

T-s Diagram

 A state of system is represented by selecting the properties i.e. temperature (T) and entropy (s) as co-ordinates as shown in Figure 2.33.

T-s DIAGRAM

A state of system is represented by selecting the properties i.e. temperature (T) and entropy (s) as co-ordinates as shown in Figure 2.33. This diagram is known as T-s diagram.

The differential form of heat transfer can be written as

dQ = Tds

When a system undergoes a change of states from state 1 to state 2, then the area under the process 1-2 represents the heat transfer from state 1 to state 2 as shown in Figure 2.33. 

Integrating above equation for state 1 to state 2,

The quantity of heat transfer (Q1-2)rev is represented by the area under T-s diagram (i.e. area 1-2-s2-s1-1).

Entropy: a Property of the System

 Let, a thermodynamic system undergoes a change of state from 1 to 2 by a reversible process 1-A-2 and returns to its original state 1 by another reversible process 2-B-1 and completing a cycle 1-2-1.

ENTROPY: A PROPERTY OF THE SYSTEM

Let, a thermodynamic system undergoes a change of state from 1 to 2 by a reversible process 1-A-2 and returns to its original state 1 by another reversible process 2-B-1 and completing a cycle 1-2-1.

For this cyclic reversible process, the entropy equation is given by

Now, let us consider the cycle 1-2-1 completed by another reversible process 2-C-1.

i.e., it is independent of the path and a function of end states only. Hence, the entropy is a property of a system.

Concept of Entropy

 Entropy is an index of unavailability or degradation of energy.

CONCEPT OF ENTROPY

Entropy is an index of unavailability or degradation of energy. It can also be stated, it is a measure of molecular disorder or random function of a system process. It can be created but it cannot be destroyed. Heat always flows from hot body to cold body and thus it becomes less value. This unavailability of energy is measured by entropy. It is an important thermodynamic property of the working substance. It increases with the addition of heat and decreases with its removal. It is the function of quantity of heat with respect to temperature.

We are usually interested in change in entropy. The change in entropy for reversible process is mathematically given by

Change in entropy, dS = Change of heat transfer / Absolute temperature = dQ / T

Unit of entropy is kJ/K or J/K

The change in entropy of a system during a process can be determined by integrating the above equation between initial and final states:

Note:- For reversible adiabatic process, the change in entropy is zero.

Clausius Inequality - Solved Anna University Problem

 Solved Anna University Problem on Clausius Inequality: Second Law and Entropy - Engineering Thermodynamics

SOLVED ANNA UNIVERSITY PROBLEM ON CLAUSIUS INEQUALITY

AU Problem 2.32

An inventor claims to have developed an engine which receives 1000 kJ at a temperature of 160°C. It rejects heat at a temperature of 5°C and delivers 0.12 kWh of mechanical work. Is this a valid claim? Justify your answer through Classius inequality.

Given data:

Q1 = 1000 kJ

T1 = 160°C = 160 + 273 = 433 K

T2 = 5°C = 5 + 273 = 278 K

W = 0.12 kWh = 0.12 × 3600 = 432 kJ

To find:

Check for validity of claim.

Solution: