Solved Anna University Problems on Heat Engines, Refrigerators and Heat Pump: Second Law and Entropy - Engineering Thermodynamics
SOLVED ANNA UNIVERSITY PROBLEMS ON HEAT ENGINES, REFRIGERATORS AND HEAT PUMP
AU Problem 2.1
In a Carnot cycle, the maximum pressure and temperature are limited to 18 bar and 410°C. The volume ratio of isentropic compression is 6 and isothermal expansion is 1.5. Assume the volume of the air at the beginning of isothermal expansion as 0.18 m3. Show the cycle on p-V and T-s diagrams and determine the
(1) pressure and temperature at main points
(2) thermal efficiency of the cycle.
Given data:
Highest pressure, p2 = 18 bar = 18 × 100 = 1800 kPa
Highest temperature, T2 = 410°C = 410 + 273 = 683K = T3
Volume, V2 = 0.18 m3
V1 / V2 = 6
V3 / V2 = 1.5
Solution:
Process 1-2:
We know that
V1 / V2 = 6
⸫ V1 = 6V2
Since the process 1-2 is isentropic compression, from the isentropic relation
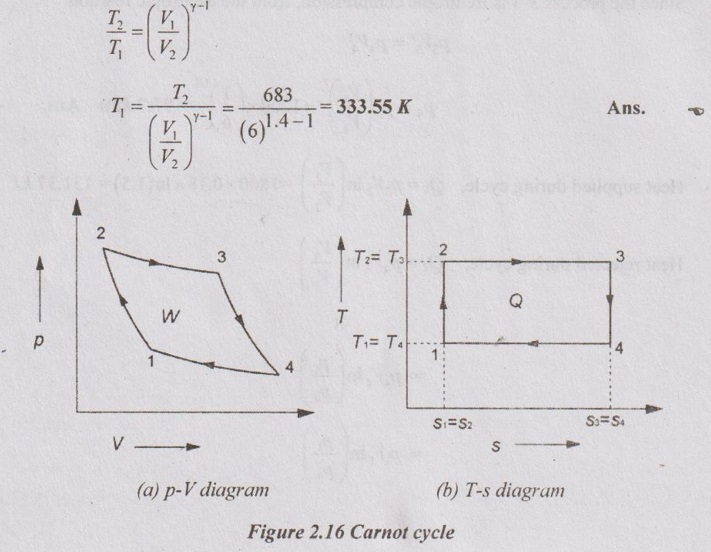
Since the process 4-1 is isothermal expansion
T1 = T4 = 333.55 K

Since the process 3-4 is isentropic compression, from the isentropic relation

AU Problem 2.2
A Carnot heat engine receives 650 kJ of heat from a source of unknown temperature and rejects 250 kJ of it to a sink as 297 K. Determine the temperature of the source and thermal efficiency of the heat engine.
Given data:
Q1 = 650 kJ
Q2 = 250 kJ
T2 = 297 K
Solution:
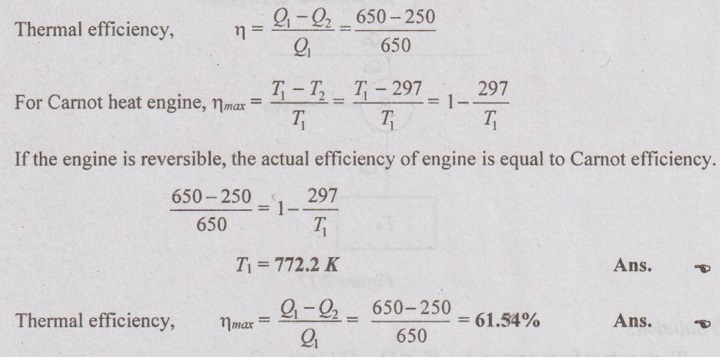
AU Problem 2.3
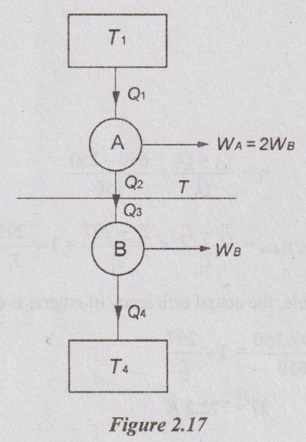
Two reversible heat engines A and B are arranged in series. Engine A rejecting heat directly to engine B. Engine A receives 200 kJ at a temperature of 421°C from a hot source while engine B is in communication with a cold sink at a temperature of 4.4°C. If the work output of A is twice that of B, find the:
(i) intermediate temperature between A and B
(ii) efficiency of each engine and
(iii) heat rejected to the cold sink.
Given data:
T1 = 421°C = 421 + 273 = 694 K
T4 = 4.4°C = 4.4 + 273 = 277.4 K
Q1 = 200 kJ
WA = 2WB
To find:
T, ηA, ηB and Q4
Solution:
Work output from engine A, WA = Q1 - Q2 = 200 - Q2
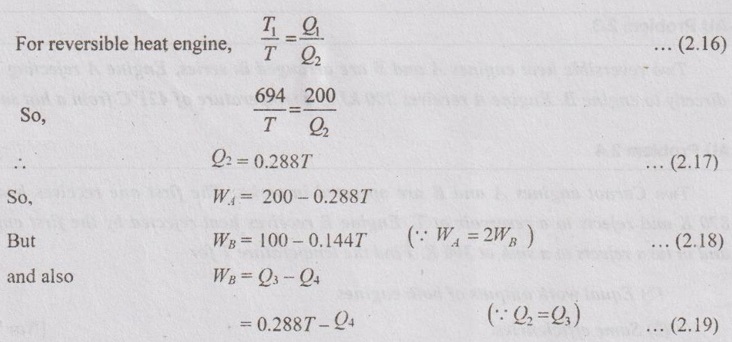
Equating equations (2.18) and (2.19),
100 - 0.144T = 0.288 T - Q4

AU Problem 2.4
Two Carnot engines A and B are operated in series. The first one receives heat at 870 K and rejects to a reservoir at T. Engine B receives heat rejected by the first engine and in turn rejects to a sink at 300 K. Find the temperature T for
(1) Equal work outputs of both engines
(2) Same efficiencies.
Same as Problem 2.9 on Page 2.25.
AU Problem 2.5
Two Carnot engines work in series between the source and sink temperatures of 550 K and 350K. If both engines develop equal power, draw the schematic and label them properly and also determine the intermediate temperature.
Similar to Problem 2.9 on Page 2.25.
[Ans:- T = 450 K]
AU Problem 2.6
An inventor claims to have developed a refrigerating unit which maintains the refrigerated space at -6°C while operating in a room where temperature is 27°C and has COP 8.5. Find out whether his claim is correct or not.
Given data:
Inventor's refrigerating unit
T3 = 27°C = 27 + 273 = 300 K
T4 = -6°C = -6 + 273 = 267 K
COPinventor = 8.5
To find:
Decision
Solution:

AU Problem 2.7
An inventor claims to have developed a refrigeration system that removes heat from the closed region at -12°C and transfers it to the surrounding air at 25°C while maintaining a COP of 6.5. Is this claim reasonable? Why?
Given data:
T4 = -12°C = -12 + 273 = 261 K
T3 = 25°C = 25 + 273 = 298 K
COPinventor = 6.5
Solution:
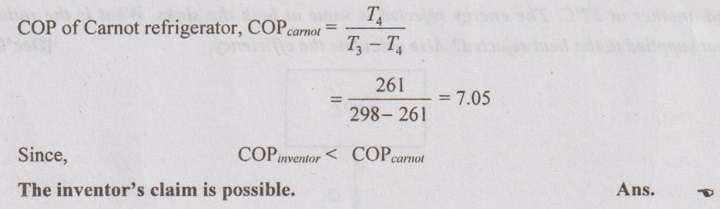
AU Problem 2.8
A heat engine operates between a source at 600°C and a sink at 60°C. Determine the least rate of heat rejection per kW net output of the engine.
Given data:
T1 = 600°C = 600 + 273 = 873 K
T2 = 60°C = 60 + 273 = 333 K
W = 1 kW
To find:
Q2/ kW net output
Solution:
For the least rate of heat rejection, the efficiency should be maximum.

AU Problem 2.9
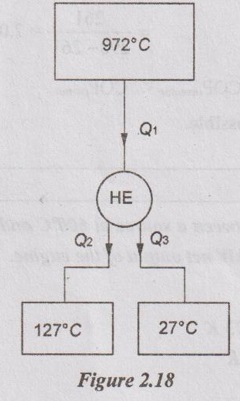
A reversible engine operates between a source at 972°C and two sinks, one at 127°C and another at 27°C. The energy rejected is same at both the sinks. What is the ratio of heat supplied to the heat rejected? Also calculate the efficiency.
Given data:
T1 = 972°C = 972 + 273 = 1245 K
T2 = 127°C = 127 + 273 = 400 K
T3 = 27°C = 27 + 273 = 300 K
Solution:
Q2 = Q3
So. Q1 = Q2 + Q3 = 2 Q2
For reversible heat engine,
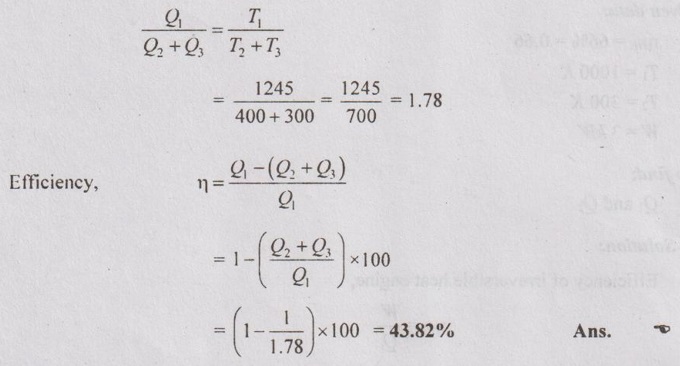
AU Problem 2.10
A reversible engine operates between a source at 972°C and two sinks, one at 127°C and another at 27°C. The energy rejected is same at both the sinks. Compute the engine efficiency. Also calculate the power and rate of heat supply if the rate of heat rejected to each sink is 100 kW.
Same as AU Problem 2.9 on Page 2.36.
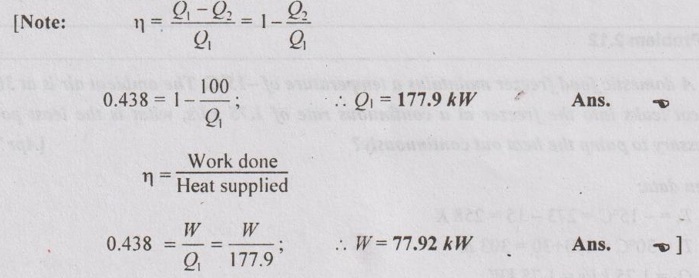
AU Problem 2.11
An irreversible heat engine with 66% efficiency of the maximum possible is operating between 1000 K and 300 K. If it delivers 3 kW of work, determine the heat extracted from the high temperature reservoir and heat rejected to low temperature reservoir.
Given data:
ηHE = 66% = 0.66
T1 = 1000 K
T2 = 300 K
W = 3 kW
To find:
Q1 and Q2
Solution:
Efficiency of irreversible heat engine,

AU Problem 2.12
A domestic food freezer maintains a temperature of -15°C. The ambient air is at 30°C. If heat leaks into the freezer at a continuous rate of 1.75 kJ/s, what is the least power necessary to pump the heat out continuously?
Given data:
T4 =-15°C = 273 – 15 = 258 K
T3 = 30°C = 273 + 30 = 303 K
Q4 =1.75 kJ/s = 1.75 kW
To find:
W
Solution:

AU Problem 2.13
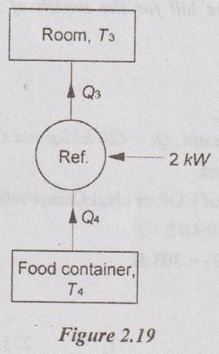
The food compartment of a refrigerator is maintained at 4°C by removing heat from it at a rate of 360 kJ/min. If the required power input to the refrigerator is 2 kW, determine the
(a) coefficient of performance of the refrigerator and
(b) rate of heat rejection to the room that houses the refrigerator.
Given data:
T4 = 4°C = 273 + 4 = 277 K
Q4 = 360 kJ/min
W = 2 kW = 2 × 60 = 120 kJ/min
To find:
COP and Q3
Solution:
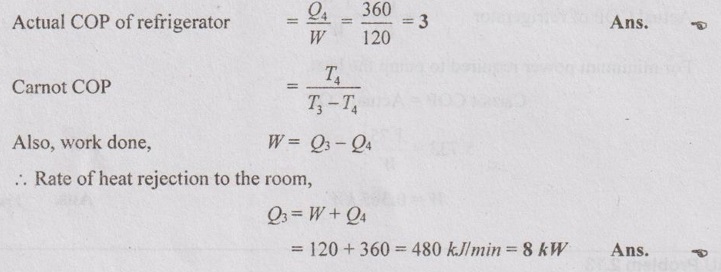
AU Problem 2.14
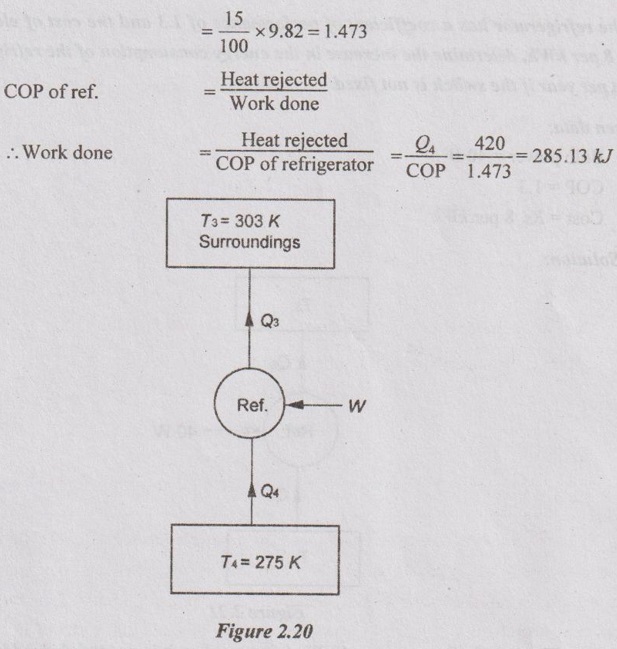
A house hold refrigerator is maintained at a temperature of 275 K. Every time the door is opened, warm material is placed inside, introducing an average of 420 kJ but making only a small change in the temperature of the refrigerator. The door is opened 20 times a day and the refrigerator operates at 15% of the ideal COP. The cost of work is Rs. 2.50 per kWh. What is the bill for the month of April for this refrigerator? The atmosphere is at 303 K.
Given data:
T4 = 275 K
Heat rejected by the refrigerator, Q4 = 420 kJ for one time
In one day = 20 times opened
COP of refrigerator = 15% of COP of ideal Carnot refrigerator.
Cost of electricity = Rs. 2.50/kWh
Atmospheric temperature, T3 = 303 K
Solution:
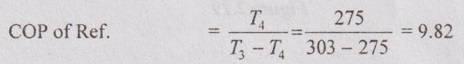
Actual COP of Ref. = 15% of COP of Carnot refrigerator
So, each time the door is opened, 285.13 kJ of work is to be done by fridge and that much electrical energy is consumed. The fridge is opened 20 times a day and April month consist of 30 days. Therefore, a fridge is opened 600 times in April month.
So, consumption for April month = 285.13 × 600 = 171079.4 kJ
Cost of electricity = 2.5 Rs./kWh = 2.5/3600 = 0.000694 Rs./kJ
Electricity charge for April month,
= 171079.4 × 0.000694 = Rs. 118.8 Ans.
AU Problem 2.15
The interior lighting of refrigerators is provided by incandescent lamps whose switches are actuated by the opening of the refrigerator door. Consider a refrigerator whose 40 W light bulb remains ON continuously as a result of a malfunction of the switch. If the refrigerator has a coefficient of performance of 1.3 and the cost of electricity of the Rs. 8 per kWh, determine the increase in the energy consumption of the refrigerator and its cost per year if the switch is not fixed.
Given data:
Bulb power = 40 W
COP = 1.3
Cost = Rs. 8 per kWh
Solution:
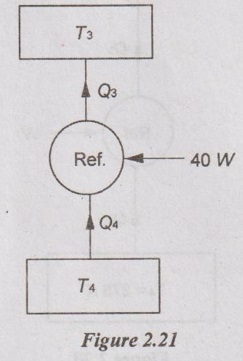
The light bulb consumes 40 W of power when it is on, and thus adds 40 W to the heat load of the refrigerator. So, Q4 = 40 W.
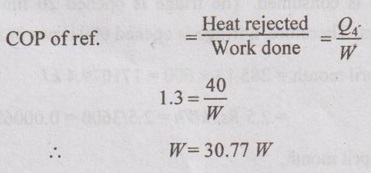
The power consumed by the refrigerator to remove the heat generated by the light bulb is 30.77 W.
Therefore, the total additional power consumed by the refrigerator is calculated by
Total power, W = 40 + 30.77 = 70.77 W = 0.07077 kW
Total number of hours in a year = 24 × 365 = 8760 hrs
Increase in energy consumption,
Q3 = 0.0707 × 8760 = 619.9 kWh/year Ans.
Increase in cost of electricity = 619.9 × 8 = Rs. 4959.2 Ans.
AU Problem 2.16
The interior lighting of refrigerators is provided by incandescent lamps whose switches are actuated by the opening of the refrigerator door. Consider a refrigerator whose 40 W light bulb remains on continuously as a result of a malfunction of the switch. If the refrigerator has a coefficient of performance of 1.3 and the cost of electricity is Rs. 5 per kWh, determine the increase in the energy consumption of the refrigerator and its cost per year if the switch is not fixed. Assume the refrigerator is opened 20 times a day for an average of 30 s.
Given data:
Power, W = 40 W
COP = 1.3
Cost of electricity = Rs. 5 per kWh
The refrigerator is opened 20 times a day for an average of 30 s
Solution:
The light bulb consumes 40 W of power when it is on, and thus adds 40 W to the heat load of the refrigerator. So, Q4 = 40 W.
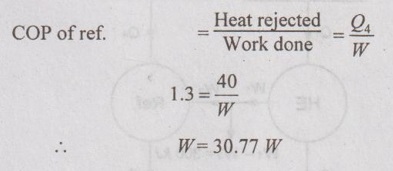
The power consumed by the refrigerator to remove the heat generated by the light bulb is 30.77 W. Therefore, the total additional power consumed by the refrigerator is
Total power, W = 40 + 30.77 = 70.77 W = 0.07077 kW
Assuming that the refrigerator is opened 20 times a day for an average of 30 s,
So, normal operating hours in a year,
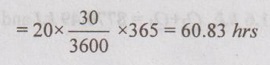
Missing 2.44
Total number of hours in a year = 24 x 365 = 8760 hrs
Then the additional hours the light remains on as a result of the malfunction becomes
=
Additional operating hours - Annual hours - Normal operating hours = 8760-60.83 = 8699.17 hrs
Increase in energy consumption,
23=0.0707x8699.17 = 615 kWh/year Ans.
Increase in cost of electricity = 615 x 5 = Rs. 3075
Ans.
AU Problem 2.17
A reversible heat engine operates between two reservoirs at 820°C and 27°C. Engine drives a reversible refrigerator which operates between reservoirs at temperatures of 27°C and -15°C. The heat transfer to the engine is 2000 kJ and network available for the combined cycle is 300 kJ. (1) How much heat is transferred to the refrigerant? and determine the total heat rejected to the reservoir at 27°C. (2) If the efficiency of the heat engine and COP of the refrigerator are each 40% of their maximum values, determine heat transfer to the refrigerator and also heat rejected to the reservoir at 27°C.
WI
T1 = 820°C
T4=-15°C
Q1
Q4
nob
W1
W2
HE
Ref.
W1- W2= 300 kJ
Q2
Q3
T2 =T3 = 27°C ibbe ist
Figure 2.22
Similar to Problem 2.5 on Page 2.22.
[Ans:- Q4 = 8221.6 kJ; Q2+Q4 = 8770.49 kJ and Q4 = 967.96 kJ; Q2+Q4 = 1655.92 kJ]
0008
Hint:
Efficiency, η = 40% ηmax = 40 ×.72.55 = 29%
COPref = 40% COP = 0.4 × 6.143 = 2.457
AU Problem 2.18
A Carnot heat engine receives heat from a reservoir at 1173 K at a rate of 800 kJ/min and rejects the waste heat to the ambient air at 300 K. The entire work output of the heat engine is used to drive a refrigerator that removes heat from the refrigerated space at 268 K and transfers it to the same ambient air at 300 K. Determine the maximum rate of heat rejection to the ambient air.
Similar to AU Problem 2.17 on Page 2.44.
[Ans:- 1918.5 kJ]
AU Problem 2.19
A Carnot heat engine works between two temperature of source at 900 K and sink at 300 K. It operates a Carnot refrigerator working between two temperatures of 300 K and 250 K. The heat engine is supplied with 50 kJ/s and it not only operates refrigerator, but also delivers a net power of 10 kW. (i) Determine the heat transferred to the refrigerant in the refrigerator and the net heat transfer to the sink maintained at 300 K. (ii) Recalculate the above, if the actual efficiency of the heat engine is 50% of the maximum value and COP of the refrigerator is 50% of the maximum value.
Similar to Problem 2.5 on Page 2.22.
[Ans:- (i) Q4 = 116.65 kJ/s; Q2 + Q4 = 156.65 kJ/s and
(ii) Q4 = 41.25 kJ/s; Q2 + Q4 = 81.25 kJ/s]
[Note: Case (ii) Efficiency of actual heat engine cycle,
η = 0.5 ηmax = 0.5 × 0.6667 = 0.33
W1 = η × Q1 = 0.33 × 50 = 16.5 kJ/s
⸫ W2 = W1 – 10 = 16.5 – 10 = 6.5 kW
COP of the actual refrigerator,
Q4 / W2 = 0.5 × 5 = 2.5
⸫ Q4 = 2.5 × 6.5 = 41.25 kJ/s
Q3 = W2 + Q4 = 6.5 + 41.25 = 47.75 kJ/s
Q2 = Q1 - W1 = 50 - 16.5 = 33.5 kJ/s
⸫ Net heat transferred to the reservoir at 300 K;
= Q2 + Q3 = 33.5 + 47.75 = 81.25 kJ/s]
AU Problem 2.20
A household refrigerator that has a power input of 450 W and a COP of 1.5 is to cool 5 large watermelons, 10 kg each, to 8°C. If the watermelons are initially at 28°C, determine how long it will take for the refrigerator to cool them. The watermelons can be treated as water whose specific heat is 4.2 kJ/kgK. Is your answer realistic or optimistic? Explain.
Given data:
Power input, W = 450 W
COP = 1.5
Number of watermelons, n = 5
So Mass of watermelon, m = 10 kg
T3 = 28°C = 273 + 28 = 301 K
T4 = 8°C = 273 + 8 = 281 K
Solution:
Heat removed from watermelons,
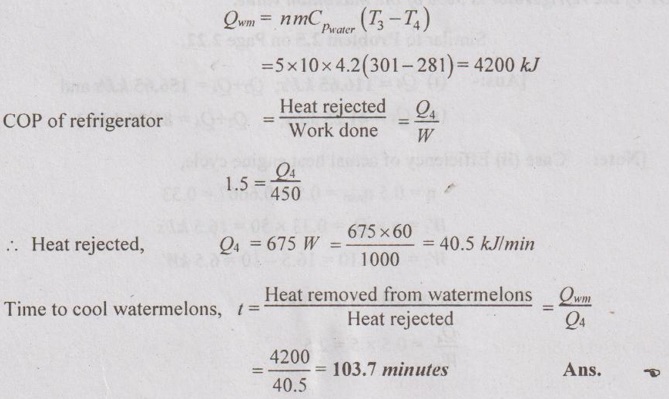
AU Problem 2.22
A heat pump operates on a Carnot heat pump cycle with a COP of 8.7. It keeps a space at 24°C by consuming 2.15 kW of power. Determine the temperature of the reservoir from which the heat is absorbed and heating load provided by the heat pump.
Given data:
Carnot COP of H.P = 8.7
T3 = 24°C = 24 + 273 = 297 K
Power consumption or work done, W = 2.15 kW
Solution:
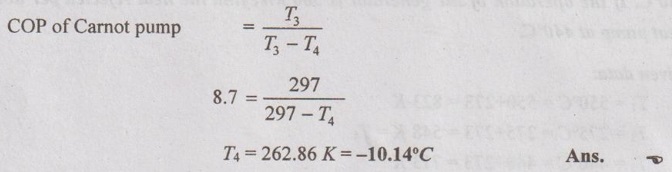
We know that for reversible heat pump,
Actual COP of heat pump = Carnot COP of heat pump

But work done = Q3 - Q4
Substituting Q4 in work done,
2.15 = Q3 - 0.89 Q3
= 0.11 Q3
⸫ Heating load, Q3 = 19.55 kW Ans.
AU Problem 2.23
A Carnot heat engine takes heat from an infinite reservoir at 550°C and rejects it to a sink a 275°C. Half of the work delivered by the engine is used to run generator and the other half is used to run heat pump which takes heat at 275°C and rejects it at 440°C. Express the heat rejected at 440°C by the heat pump as % of heat supplied to the engine at 550°C. If the operation of the generator is 500 kW, find the heat rejected per hour by the heat pump at 440°C.
Given data:
T1 = 550°C = 550 + 273 = 823 K
T2 = 275°C = 275 + 273 = 548 K = T4
T3 = 440°C = 440 + 273 = 713 K
Wg = 500 kW
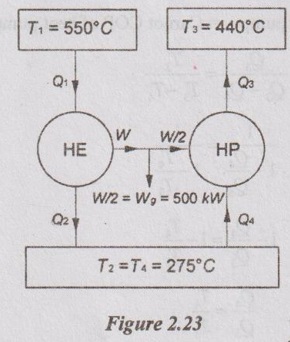
To find:
Q3 / Q1 and Q3
Solution:
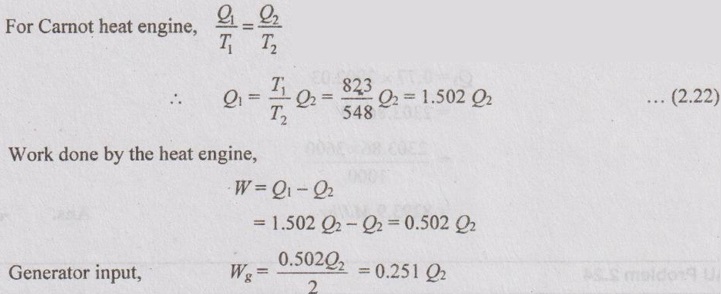
Work input to the heat pump,
WHP = 0.251 Q2
Work input to the heat pump,
WHP = Q3 - Q4
Heat rejected by the heat pump,
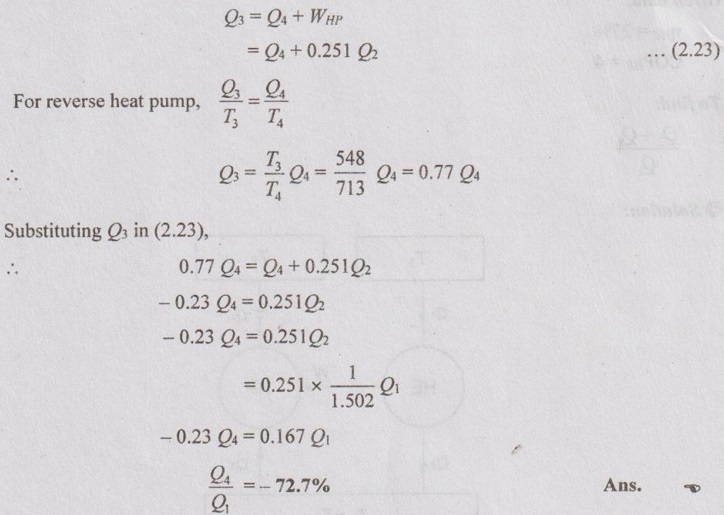
The generator power input, Wg = 500 kW
0.251 Q2 = 500
Q2 = 1992.03 kW
⸫ Q1 = 1.502 Q2 = 1.502 × 1992.03 = 2992.03 kW

AU Problem 2.24
A heat engine is used to drive a heat pump. The heat transfer from the heat engine and from the heat pump is used to heat the water circulating through the radiators of building. The efficiency of the heat engine is 27% and COP of the heat pump is 4. (i) Draw the neat diagram of the arrangement and (ii) evaluate the ratio of heat transfer to the circulating water to the heat transfer to the heat engine.
Given data:
ηHE = 27%
COPHP = 4
To find:
Q2 + Q3 / Q1
Solution:
AU Problem 2.25
A heat engine operating between two reservoirs at 1000 K and 300 K is used to drive heat pump which extracts heat from the reservoir at a rate twice that at which engine rejects heat to it. If the efficiency of the engine is 40% of the maximum possible and the coefficient of performance of the heat pump is 50% of the maximum possible, make calculations for the temperature of the reservoir to which the heat pump rejects heat. Also work out the rate of heat rejection from the heat pump if the rate of supply of heat to the engine is 50 kW.
Given data:
T1 = 1000 K
T2 = 300 K
Q4 = 2 Q2
Efficiency of heat engine, ηHE = 40% of maximum possible efficiency
COP of heat pump = 50% of maximum possible COP
Rate of supply to heat engine, Q1 = 50 kW
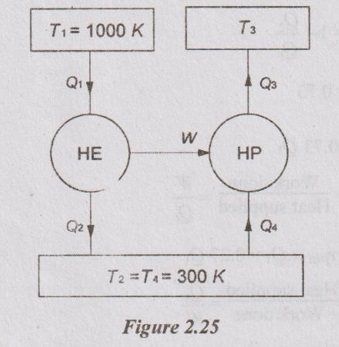
To find:
Q3 and T3
Solution:

AU Problem 2.26
A heat pump working on the Carnot cycle takes in heat from a reservoir at 5°C and delivers heat to a reservoir at 60°C. A heat engine is driven by a source at 840°C and rejects heat to a reservoir at 60°C. The reversible heat engine, in addition to drive the heat pump, also drives a machine that absorbs 30 kW. If the heat pump extracts 17 kJ/s from the 5°C reservoir, determine (1) the rate of heat supply from the 840°C source and (2) the rate of heat rejection to the 60°C sink. [Nov '11 & May'17
Given data:
T1 = 840 + 273 = 1113 K
T2 = 60 + 273 = 333 K
T1 = 5 + 273 = 278 K
T3 = 60 + 273 = 333 K
Q4 = 17 kJ /s = 17 kW
W3 = 30 kW
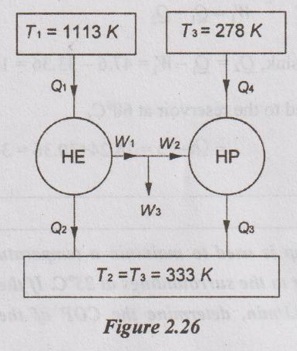
To find:
Q1 and Q2 + Q3
Solution:

Work input to the heat pump, W2 = Q3 - Q4 = 20.36 – 17 = 3.36 kW
It is given that W1 = W2 + W3 = 3.36 + 30 = 33.36 kW
Maximum efficiency of heat engine,
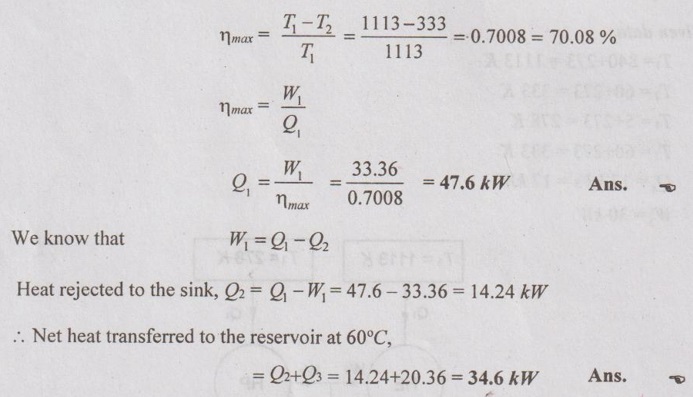
AU Problem 2.27
(i) A reversible heat pump is used to maintain a temperature of 0°C in a refrigerator when it rejects the heat to the surroundings at 25°C. If the heat removal rate from the refrigerator is 1440 kJ/min, determine the COP of the machine and work input required.
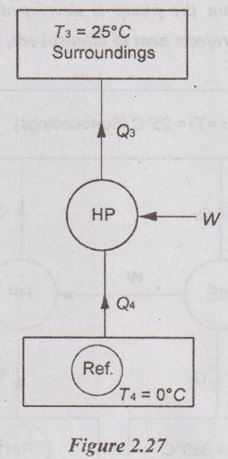
Given data:
T3 = 25°C = 25 + 273 = 298K
T4 = 0°C = 0 + 273 = 273K
Q4 = 1440 kJ/min = 1440/60 = 24 kW
To find:
COP and W
Solution:
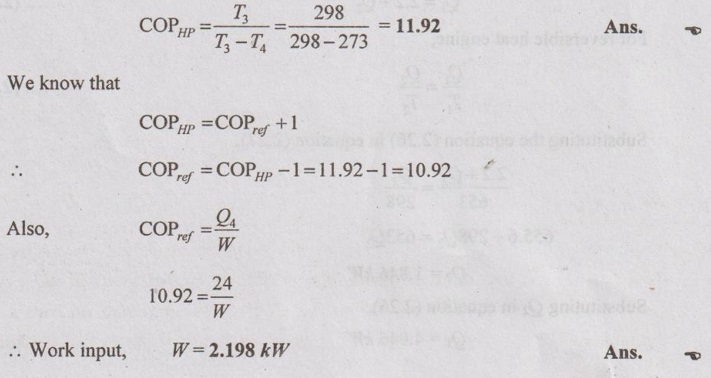
(ii) If the required input to run the pump is developed by a reversible engine which receives heat at 380°C and rejects heat to atmosphere, then determine the overall COP of the system.
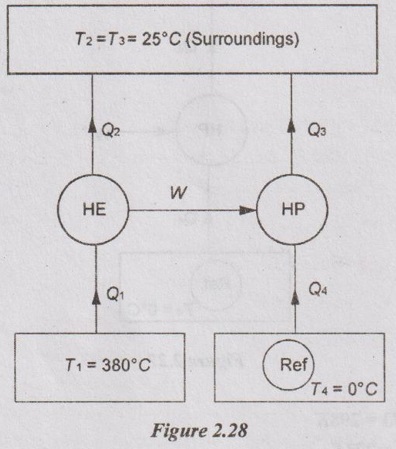
For heat pump, Q3 = Q4 + W = 24 + 2.2 = 26.2 kW
We know that the work output of the heat engine is equal to the work input supplied to heat pump.
W = Q1 - Q2 = 2.2 kW

AU Problem 2.28
An engine is supplied with 1120 kJ/s of heat. The source and sink temperature are maintained at 560 K and 280 K. Determine whether the following cases represent the reversible, irreversible or impossible heat engines.
(i) 900 kW of heat rejected
(ii) 560 kW of heat rejected
(iii) 108 kW of heat rejected.
Same as Problem 2.3 on Page 2.19.
AU Problem 2.29
Two heat engines operating in series are giving out equal amount of work. The total work is 50 kJ/cycle. If the reservoirs are at 1000 K and 250 K, find the intermediate temperature and efficiency of each engine. Also, find the heat extracted from the source.
Given data:
T1 = 1000 K
T4 = 250 K
WA = WB
W = WA + WB = 50 kJ/cycle
To find:
(i) Intermediate temperature, T
(ii) Efficiency of each engine, ηA and ηB
(iii) Heat extracted from the source, Q1.
Solution:
Let, Q1 and Q2 = Heat supplied to and rejected from HE-A
Q3 and Q4 = Heat supplied to and rejected from HE-B
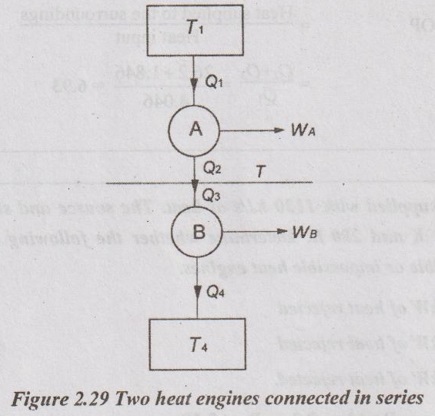
For the given condition, WA = WB
WA = Q1 - Q2 and WB = Q3 - Q4

For reversible heat engine, the actual engine efficiency is equal to Carnot efficiency.
So, the efficiency of engine A,
If the total work output from a series of reversible engines is equal to the work output from an engine operating between the same temperature limits,

AU Problem 2.30
A reversible heat engine operates between two reservoirs at temperature of 600°C and 40°C. The engine drives a reversible refrigerator which operates between reservoirs at temperatures of 40°C and -20°C. The heat transfer to the heat engine is 2000 kJ and the network output for the combined engine refrigerator is 360 kJ. Calculate the heat transfer to the refrigerant and the net heat transfer to the reservoir at 40°C.
Similar to Problem 2.5 on Page 2.22.
[Ans:- 5539 kJ and 1899.6 kJ]
AU Problem 2.31
A Carnot heat engine draws heat from a reservoir at temperature 600 K and rejects heat to another reservoir at temperature T3. The Carnot forward cycle engine drives a Carnot reversed cycle engine or Carnot refrigerator which absorbs heat from reservoir at temperature 300 K and rejects heat to a reservoir at temperature T3. Determine:
(i) The temperature T3 such that heat supplied to engine Q1, is equal to the heat absorbed by refrigerator Q2.
(ii) The efficiency of Carnot engine and C.O.P of Carnot refrigerator.
Given data:
T1 = 600 K
T2 = 300 K
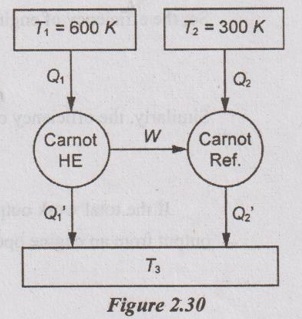
Solution:
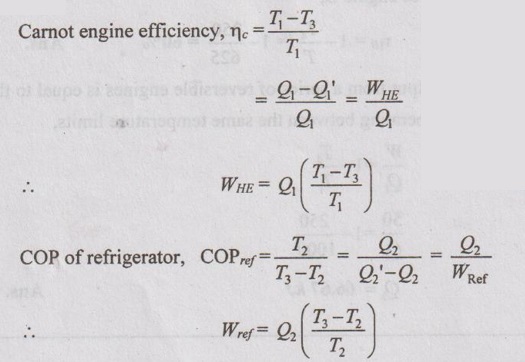
As heat supplied to engine is equal to the heat absorbed by refrigerator,
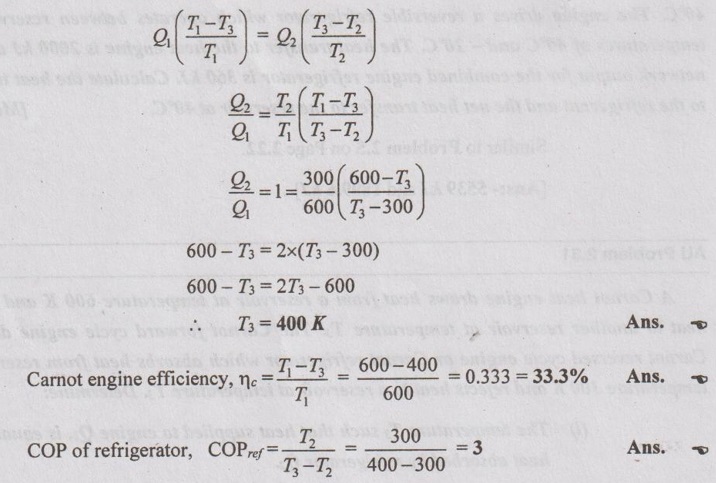
No comments:
Post a Comment