1. What is a real gas? Give example.
The gas which does not obey the law of equation of state is known as real gas. All practical gases are real gas.
2. What is known as equation of state and when it can be used for engineering calculations?
The relationship which exists for the state variables of the system in equilibrium is called equation of state.
The equation of state for ideal is given by
pV = mRT
where
p = Pressure of gas, Pa
V = Volume of gas, m3
m = Mass of gas, kg
R = Gas constant, kJ/kgK
T = Temperature, K.
(i) The equations of state are used in process engineering problems which are mainly needed in petroleum industries.
(ii) The equation of state helps to determine the state of the flow regime, the parameters for handling the reservoir fluids, piping and sizing.
(iii) The equation of state is applied for PVT and VLE calculations of different pure fluids and fluid mixtures.
3. Determine the molecular volume of any perfect gas at 600 N/m2 and 30°C. Universal gas constant may be taken as 8314 J/kg mole-K.
Given data:
p = 600 N/m2 = 0.6 kN/m2
T = 30°C = 30 + 273 = 303 K
R = 8314 J/kmol K = 8.314 kJ/kmol K
Solution:
Ideal gas equation, pv=RT
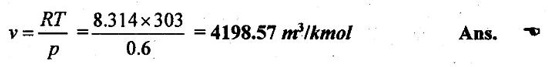
4. State Boyle's law.
Boyle's law states, "the volume of a given mass of a gas varies inversely as its absolute pressure when the temperature remains constant".
v α 1/p (or) pv = constant as long as temperature is constant.
5. State Charle's law.
Charle's law states, "the volume of a given mass of a gas varies directly as its absolute temperature when the pressure remains constant".
v α T (or) v/T = constant as long as pressure is constant.
6. State Joule's law.
Joule's law states, "the internal energy of a given quantity of a gas depends only on the temperature".
7. State Regnault's law.
Regnault's law states that specific heats of a gas always remain constant.
8. State Avogadro's law.
Avogadro's law states, “equal volumes of different perfect gases at the same temperature and pressure contain equal number of molecules".
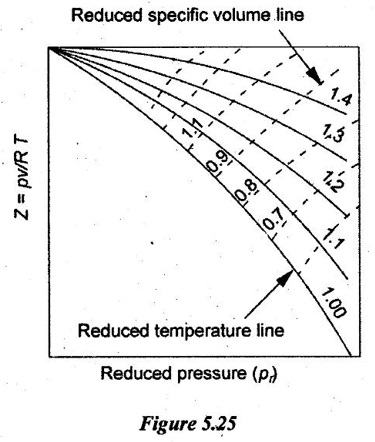
9. State the principle of corresponding states.
Substances behave alike at the same reduced states. Substances at same reduced states are at corresponding states. It is called principle of corresponding states.
According to van der Waals, the principle of corresponding states indicates that all fluids, when compared at the same reduced temperature and reduced pressure, have approximately the same compressibility factor and all deviate from ideal gas behavior to about the same degree.
The equation of state for real gases is given by
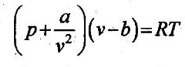
For ideal gas, the constants a and b are zero. The values of a and b are dependent on the type of fluid or gases used.
10. What are reduced properties? Give their significance.
Each gas behaves in its own way for the given pressure and temperature. So, the correction factor can be set for each property of gas such as pressure, p and temperature, T to know the thermodynamic behaviour for any gas by normalizing the properties. Therefore, the pressure, p and temperature, T is normalised with respect to their critical values such as pc and Tc.
So, the correction factors of pressure and temperature are called reduced properties. The normalised pressure, pr is called reduced pressure and the normalised temperature Tr is called reduced temperature.
Significance:
(i) It provides reasonable accuracy near the critical point.
(ii) It describes the behaviour of physical quantities near continuous phase transitions in critical exponents.
11. How does the Van der Waals equation differ from the ideal gas equation of state?
The ideal gas equation of state is based on the fact that the molecules of a gas as point particles with perfectly elastic collisions. Van der Waals equation takes into account of the following factors:
1. Intermolecular interactive forces.
2. Shape factor is considered.
12. What is meant by virtual expansion?
Virial or virtual expansions are only applicable to gases of low and medium densities.
The equation state of a substance is given by
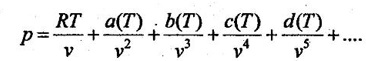
The coefficients of a(T), b(T), c(T), d(T) .... are virtual coefficients. The virtual coefficient will vanish when the pressure becomes zero. Finally, the equation of state reduces to ideal-gas equation.
13. Have you ever encountered any ideal gas? If so, where?
No. In actual practice, there is no ideal gas which strictly follows the gas laws over the entire range of temperature and pressure. However, hydrogen, oxygen, nitrogen and air behave as an ideal gas under certain temperature and pressure limits.
14. Distinguish between ideal and real gas.
An ideal gas strictly follows the gas laws under all conditions of temperature and pressure. The real gas does strictly not follow the gas laws under all conditions of temperature and pressure.
15. What are the assumptions made to drive ideal gas equation analytically using the kinetic theory of gases?
1. There is no intermolecular force between particles.
2. The volume of the molecules is negligible in comparison with the gas.
16. Show that Cp-CR for an ideal gas.
In a thermodynamic process, according to the conservation of energy, the first law of thermodynamics can be expressed by
Heat transfer = Work done + Change in internal energy
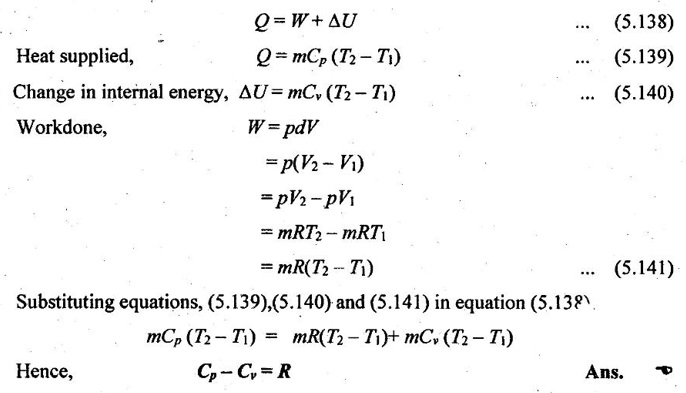
17. When does real gas behave like ideal gas and why?
If the pressure of real gas tends to zero or temperature tends to infinity, the real gas behaves as an ideal gas, because the potential energy due to intermolecular forces becomes less significant compared with the particles' kinetic energy, and the size of the molecules becomes less significant compared to the empty space between them.
18. What are the two distinct features of real gas?
Real gases are made up of molecules or atoms which occupies some space. It has a definite volume even they are extremely small.
The collision of particles is non-elastic. Since they are made up particles or molecules, they may attract one another very strongly with the expense of repulsive energy or attractive force. Due to this, there is loss in kinetic energy.
19. What are known as thermodynamic gradients?
Thermodynamic gradients are mathematical interrelations which are used to determine the change in thermodynamic properties i.e, pressure, temperature and volume, for the systém having constant chemical composition. So, thermodynamic gradients are partial derivatives.
20. List various thermodynamics potentials used for deriving Maxwell's relations.
Various thermodynamics potentials used for deriving Maxwell's relations are: Internal Energy (u), Enthalpy (h), Helmholtz function (a) and Gibbs function (G).
21. What are Maxwell relations?
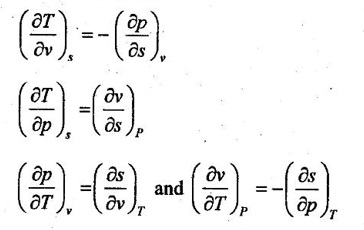
These are known as Maxwell relations. These equations are derived by using first law of thermodynamics, Helmotz's function (a = u - Ts), and Gibbs function (G = h − Ts).
22. Write down two Tds relations.
The equation (5.142) is known as the first form of entropy equation (or) the first Tds equation.
The equation (5.143) is known as the second form of entropy equation (or) the second Tds equation.
23. What is coefficient of volume expansion?
Coefficient of volume expansion is defined as the change in volume with change in temperature per unit volume by keeping pressure constant. It is denoted by β.
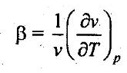
24. Define Joule-Thomson coefficient.
Joule-Thomson coefficient is defined as the ratio of change in temperature to change in pressure by keeping enthalpy constant.
It is denoted by the relation
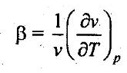
25. What is the importance of Joule-Thomson coefficient?
Joule-Thomson coefficient describes the temperature change of a real gas or liquid when it is forced through a valve or porous plug while keeping insulated so that there is no heat exchanged with the environment.
⸫ μ = 0. It implies that the Joule-Thomson coefficient is zero for ideal gas.
26. What does Joule-Thomson coefficient represent?
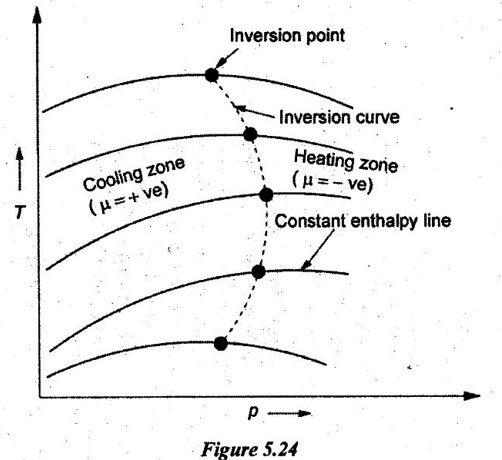
The Joule-Thomson co-efficient represents the change in temperature with change in pressure by keeping enthalpy constant as shown in Figure 5.24.
27. Define isothermal compressibility.
Isothermal compressibility is defined as the change in volume with change in pressure per unit volume by keeping temperature constant. It is denoted by K
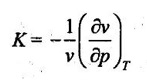
28. Show that Joule Thomson coefficient is zero for an ideal gas.
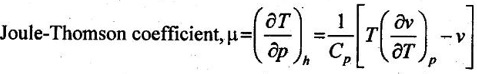
We know that the equation of state is written as
pv = RT
Differentiating the above equation of state with respect to T by keeping pressure, p constant,
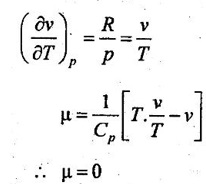
It implies that the Joule-Thomson coefficient is zero for ideal gas.
29. Define compressibility factor.
The perfect gas equation is pv = RT. But for real gas, a correction factor has to be introduced in the perfect gas equation to account the deviation of real gas from the perfect gas equation. This factor is known as compressibility factor (Z) and is defined by Z = pv / RT.
30. What does Van der Waals equation signify? What is its value for an ideal gas at critical point?
1. Correction for intermolecular attraction.
2. Correction for molecular volume in terms of Shape factor.
At critical point, the Van der Waals equation becomes
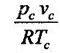= 1 for ideal gases
31. Draw the generalized compressibility chart.
32. What is the compressibility factor of Vander Waals' gas at critical point?
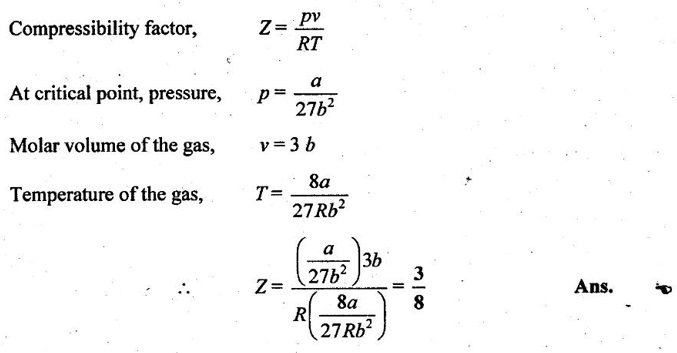
33. Write the Clausius-Clapeyron equation and label all the variables.
Clapeyron equation involves in the relationship between saturation pressure and saturation temperature. The enthalpy of evaporation and the specific volume of the two phases are also involved.
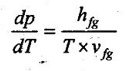
where
dp = Change in pressure, kPa
dT = Change in temperature, K
hfg = Enthalpy of vapourisation, kJ/kg
T = Absolute temperature, K
vfg = Specific volume of vapourisation, m3/kg.
34. Identify the application of Clausius - Clapeyron equation.
This equation provides a basis for the calculation of properties in a two-phase region. This equation can be applied to sublimation process.
35. Using Clausius-Clapeyron equation, estimate the enthalpy of vaporization at 200°C, vg = 0.1274 m3/kg, vƒ = 0.001157 m3/kg, dp/dT = 32 kPa/K.
Given data:
Ts = 200°C = 200 + 273 = 473 K
vg = 0.1274 m3/kg
v = 0.001157 m3/kg
(dp/dT) = 32 kPa/K
Solution:
By Clausius-Clapeyron equation,
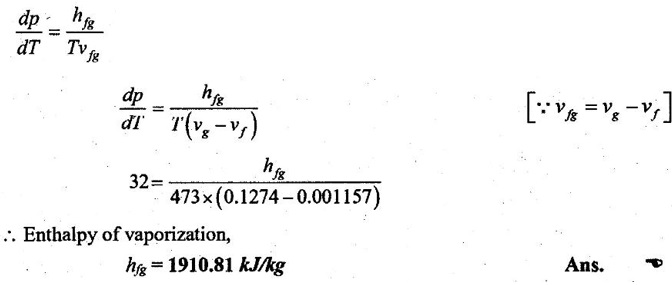
36. State Helmholtz function.
Helmholtz function is property of a system and it is given by subtracting the product of absolute temperature (T) and entropy (s) from the internal energy u.
i.e. Helmholtz function = u – Ts
37. State Gibbs function.
Gibbs function is property of a system and is given by
G = u - Ts + pv = h – Ts [⸪ h = u + pv ]
where
h = Enthalpy, kJ/kg
T = Temperature, K
s = Entropy, kJ/kgK.
38. Define molar mass.
Molar mass is a physical property. It is defined as the ratio of the mass of a given substance to the total amount of substance.
Molar mass, M = Mass of a given substance / Total amount of substance
39. Using the definition of mass and mole fractions derive a relation between them.
1. Mass fraction:
If a gas mixture consists of gases 1, 2, 3 and so on, the mass of the mixture is the sum of masses of the component gases.
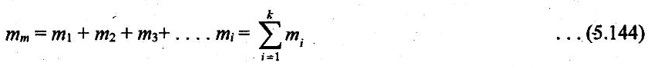
The mean fraction or mass fraction of any component is defined as the ratio of mass of a component (mi) to the mass of the mixture (mm). Mathematically,
xi = mi / mm
In mass or gravimetric analysis, the mass of each component is specified.
2. Molar fraction:
Molar fraction is the ratio of the number of moles of a component (Ni) to the total number of moles of the mixture (Nm). The total number of moles of a mixture is the sum of the number of its components.
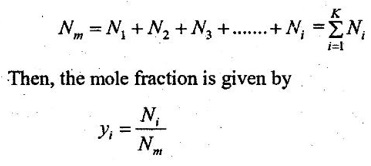
In molar analysis, the moles of each component are specified. The number of moles N, the mass m, and the molar mass M of a component and mixture is related by
40. What is the partial pressure of carbon dioxide in a container that holds 5 moles of carbon dioxide, 3 moles of nitrogen and 1 mole of hydrogen and has a total pressure of 1.05 atmospheres?
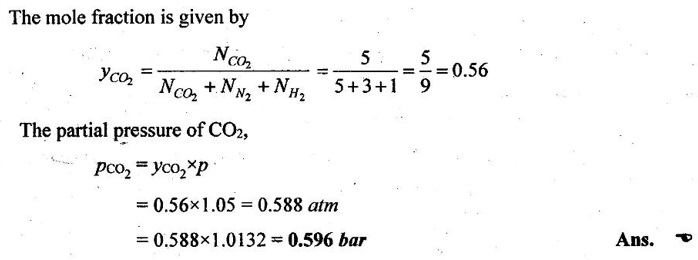
41. What is Amagat's law?
According to Amagat's law of partial volumes, the volume of a gas mixture is equal to the sum of the volume of each gas if each gas is existed alone at the temperature and pressure of the mixture.
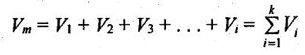
where Vm - Volume of mixture
V1, V2, ... Vi = Volume of each component in mixture.
42. In a gas mixture, which component will have the higher partial pressure the one with the higher mole number or the one with the larger molar mass?
In a gas mixture, the component having larger molar mass will have the higher partial pressure.
43. How many molecules are present in 10 g of hydrogen?
There are 10 molecules present in 10 g of hydrogen.
44. Identify the relationship between the partial pressures of the constituents in gas mixtures.
The sum of partial pressures of the components of a gas mixture is equal to the mixture pressure. The partial pressure pi of a component i in a gas mixture is given by
pi = yipm
where yi = Mole fraction
pm = Mixture pressure
Σpi = Σyi pm = pm Σyi = pm
This relation applies to any gas mixtures whether it is an ideal gas or not.
45. How does gas constant depend on molecular mass of the gas?
If we look at the Ideal Gas equation,
pv = mRT
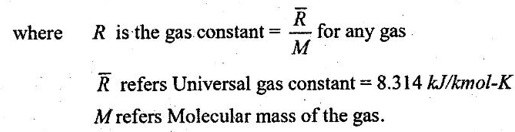
Therefore, gas constant depend on molecular mass of the gas.
For example, the gas constant R for oxygen is calculated by
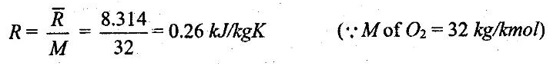
No comments:
Post a Comment