Solved Anna University Problems on closed systems (Non – Flow Processes)

 Solved Anna University Problems on closed systems (Non – Flow Processes): Basics, Zeroth and First Law - Engineering Thermodynamics

SOLVED ANNA UNIVERSITY PROBLEMS ON CLOSED SYSTEMS (NON – FLOW PROCESSES)

AU Problem 1.13

A stationary mass of a gas is compressed without friction from an initial state of 0.3 m3 and 0.105 MPa to a final state of 0.15 m3 and 0.105 MPa, the pressure remaining constant during the process. There is a transfer of 37.6 kJ of heat from the gas during the process. How much does the internal energy of the gas change?

Given data:

V1 = 0.3 m3

p1 = 0.105 MPa = 105 kPa

V2 = 0.15 m3

p2 = 0.105 MPa = 105 kPa

Q = -37.6 kJ (Negative sign is due to transfer of heat from the gas)

To find:

Change in internal energy, ΔU

Solution:

We know that for constant pressure process,

Work done, W = p (V2 - V1) = 105 × (0.15 - 0.3) = -15.75 kJ 

From first law, Q = W + ΔU

-37.6 = -15.75 + ΔU

⸫ ΔU = -21.85 kJ       Ans.

Note:- Here, negative sign indicates that the internal energy of the system decreases by 21.85 kJ.

AU Problem 1.14

A gas of mass 1.5 kg undergoes a quasi-static expansion which follows a relationship p = a+bV, where a and b are constants. The initial and final pressures are 1000 kPa and 200 kPa respectively and the corresponding volumes are 0.2 m3 and 1.2 m3. The specific internal enrgy of the gas is given by the relation u = (1.5pv - 85) kJ/kg, where p is in kPa and v is in m3/kg. Calculate the net heat transfer and maximum internal energy of the attained during expansion.

Given data:

m = 1.5 kg 

p = a + bV

p1 = 1000 kPa

gas

p2 = 200 kPa

V1 = 0.2 m3

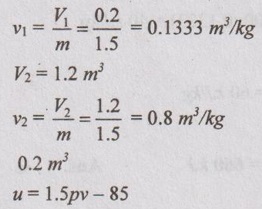
To find:

Heat transfer, Q and maximum internal energy, ΔU

Solution:

p1 = a + bV1

1000 = a + 0.2b           ... (1.60)

p2 = a + bV2

200 = a + 1.2b               ... (1.61)

(1.60) - (1.61),   800 = -b

⸫ b = -800

Substituting the value of b = -800 to equation (1.60), it becomes,

a = 1160

⸫ The relationship p = a+bV becomes,

p = 1160 - 800V      ... (1.62)

Work transfer,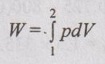  

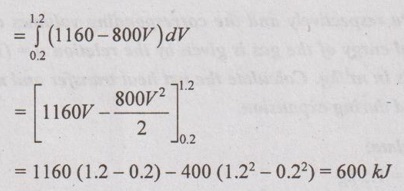
Change in internal energy,

Δu = u2 - u1

= (1.5p2v2 - 85) - (1.5p1v1 - 85)

= (1.5 p2v2 -1.5 p1v1) = 1.5( p2v2 - p1v1)

= 1.5(200 × 0.8 - 1000 × 0.1333) = 40 kJ/kg

Total change in internal energy,

ΔU = m Δu = 1.5 × 40 = 60 kJ/kg

According to the first law of thermodynamics,

Heat transfer, Q = W + ΔU = 600 + 60 = 660 kJ   Ans.

Substituting the equation (1.62) in u = 1.5pv - 85,

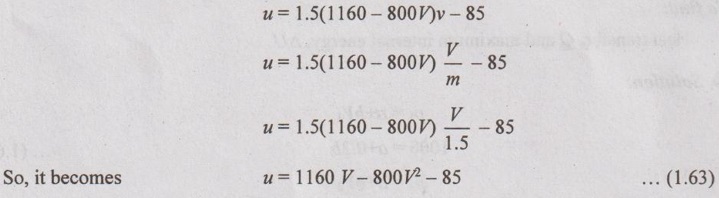
To find the maximum internal energy, differentiating the equation (1.63) with respect to V and equating it to zero.

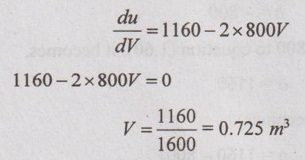
From the equation (1.63), umax = 1160 × 0.725 - 800(0.725)2 - 85 = 335.5 kJ/kg

⸫ Umax = m umax = 1.5 × 335.5 = 503.25 kJ    Ans.

AU Problem 1.15

A fluid is confined in a cylinder by a spring-loaded frictionless piston so that the pressure in the fluid is a linear function of the volume (p = a + bV). The internal energy of the fluid is given by the following equation U = 34 + 3.15pV, where U is kJ, p is in kPa and V in m3. If the fluid changes from an initial state of 170 kPa, 0.03 m3 to a final state of 400 kPa, 0.06 m3, with no other work than that done on the piston, find the direction and magnitude of the work and heat transfer. 

Given data:

p = a + bV

U = 34 + 3.15pV 

p1 = 170 kPa

V1 = 0.03 m3

p2 = 400 kPa

V2 = 0.06 m3

To find:

Work transfer, W and heat transfer, Q

Solution:

Change in internal energy, ΔU = U2 - U1 = (34 + 3.15 p2V2) - (34 + 3.15 p1V1) 

= 3.15 (p2V2 - p1V1)

= 3.15 (400 × 0.06 - 170 × 0.03) = 59.54 kJ

From pressure equation, p = a + bV

At initial state, p1 = a + bV1               ... (1.64)

170 = a + 0.03b              ... (1.65)

At final state, p2 = a + bV2              ... (1.66)

400 = a + 0.06b               ... (1.67)

 (1.67) - (1.65) results,

230 = 0.03b

⸫ b = 7666.67

Substituting the value of b in (1.65),

170 = a + 0.03 (7666.67)

a = -60.0

⸫ The pressure equation, p = -60 + 7666.67 V

Work done,

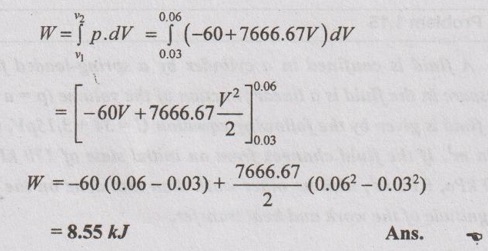
 (Positive sign indicates that the work is done by the system.)

By first law of thermodynamics,

Q = W + ΔU = 8.55 + 59.54 = 68.09 kJ Ans.

(Positive heat transfer indicates that the heat is transferred into the system.)

AU Problem 1.16

A work done by substance in a reversible non-flow manner is in accordance with V = (15/p) m3, where p is in bar. Evaluate the work done on or by the system as pressure increases from 10 bar to 100 bar. Indicate whether it is a compression process or expansion process. If the change in internal energy is 500 kJ, calculate the direction and magnitude of heat transfer.

Given data:

V = 15/p m3

p1 = 10 bar

p2 = 100 bar

ΔU = 500 kJ

Solution:

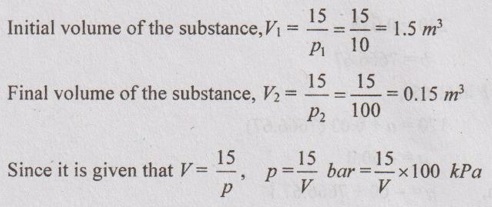
Work done by the system,

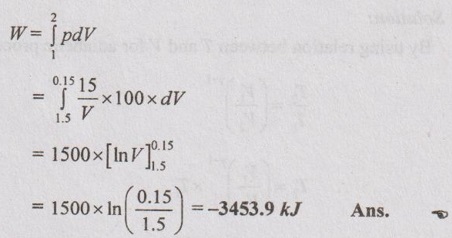
The negative sign indicates the work is done on the system and the process is a compression process.     Ans.

By first law of thermodynamics,

Q = W + ΔU

Q = -3453.9 + 500 = -2953.9 kJ        Ans.

The negative sign indicates that heat is rejected by the system. Ans.

AU Problem 1.17

0.25 kg of air at a pressure of 1 bar occupies a volume of 0.3 m3. If this air expands isothermally to a volume of 0.9 m3, find the (i) initial temperature, (ii) final temperature (iii) external Work done, (iv) heat absorbed by the air, (v) change in internal energy. Assume R = 0.287 kJ/K. 

Same as Problem 1.17 on Page 1.92.

AU Problem 1.18

One litre of hydrogen at 273 K is adiabatically compressed to one-half of its initial volume. Find the change in temperature of the gas if the ratio of two specific heats for hydrogen is 1.4.

Given data:

V1 = 1 litre = 0.001 m3

T1 = 273 K

V2 = 1/2 litre = 0.0005 m3

γ = 1.4

Process: Adiabatic process

Solution:

By using relation between T and V for adiabatic process,

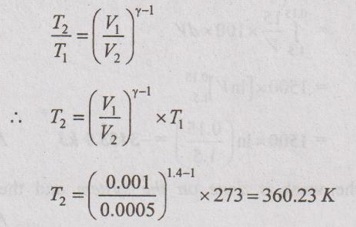
Change in temperature of the gas,

T2 - T1 = 360.23 - 273 = 87.23 K      Ans.

AU Problem 1.19

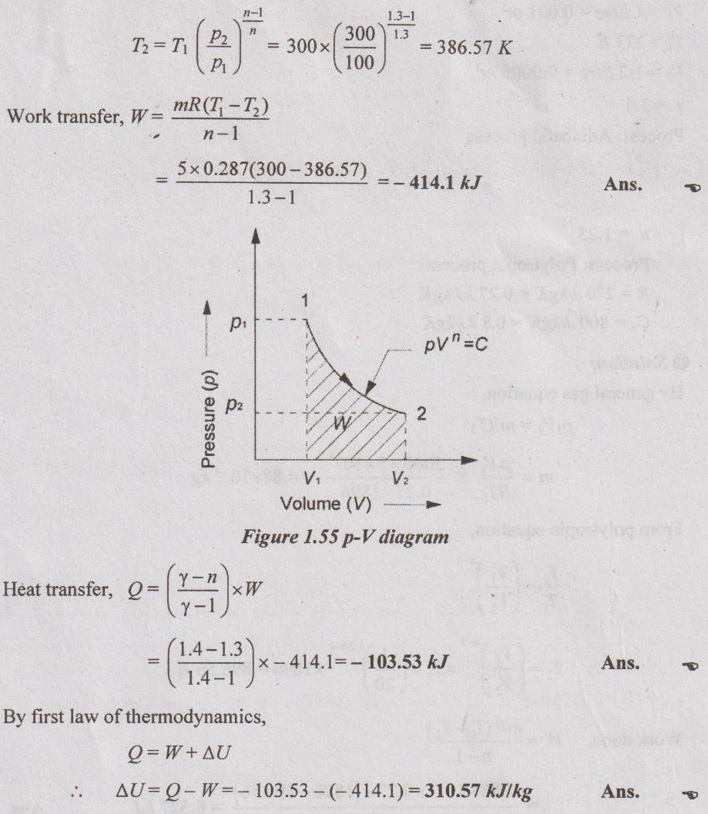
Five kg of air is compressed polytropically (n = 1.3) from 1 bar and 27°C to 3 bar. Find the (i) work transfer, (ii) heat transfer and (iii) change in internal energy. 

Given data:

m = 5 kg

p1 = 1 bar = 100 kN/m2

T1 = 27°C = 27 + 273 = 300 K

p2 = 3 bar = 300 kN/m2

n = 1.3

Process: Polytropic process

To find:

W, Q and ΔU

Solution:

From the P & T relation of polytropic process,

AU Problem 1.20

The gas expanding in the combustion space of a reciprocating engine has an initial pressure of 50 bar and an initial temperature of 1623°C. The initial volume is 50000 mm3 and the gas expands through a volume ratio of 20 according to the law pV1.25 = constant. Calculate

(i) The work transfer and

(ii) Heat transfer in the expansion process. Take R = 270 J/kgK and Cv = 800 J/kgK.

Given data:

p1 = 50 bar = 5000 kN/m2

T1 = 1623°C = 1623 + 273 = 1896 K

V1 = 50000 mm3 = 5 × 10-5 m3

V2 / V1 = 20 ⇒ V2 = 20 × V1 = 20 × 5 × 10-5 = 1 × 10-3 m3

Missing 1.144

n = 1.25

Process: Polytropic process

R = 270 J/kgK = 0.27 kJ/kgK Cy=800 J/kgK = 0.8 kJ/kgK

Solution:

By general gas equation,

pV = mRT

PV

5000×5×10-5

m =

=

4.88×104 kg

RT1

0.27×1896

From polytropic equation,

T2 T

Τ2

-

V2

n-1

n-1

mR(T-T)

Work done,

W

n-1

Engineering Thermodynamics

1.25-1

1

× T1

×1896 = 896.56 K

20

4.88×10×0.27×(1896–896.56)

= 0.527 kJ

Ans.

1.25-1

Heat transfer, Q=Wx

Y n Y-1

= 0.527x

1.4-1.25 1.4-1

= 0.1976 kJ

Ans.

AU Problem 1.21

1 kg of gas at 1.1 bar, 27° C is compressed to 6.6 bar as per the law pV1.3 Calculate work and heat transfer when the gas is:

(1) ethane (C2H6) with molar mass of 30 kg/k mol and Cp of 2.1 kJ/kgK. (2) argon (Ar) with molar mass of 40 kg/k mol and Cp of 0.52 kJ/kgK.

Given data:

m 1 kg

P1 = 1.1 bar = 110 kN/m2

Pi

T1 = 27°C=27+273 = 300 K

P2 = 6.6 bar = 660 kN/m2

Molar mass of ethane = 30 kg/kmol

= const.

[Dec '05'

Cp of ethane = 2.1 kJ/kgK

Molar mass of argon = 40 kg/kmol 

Cp of argon = 0.52 kJ/kgK

pV1.3 = C

Solution:

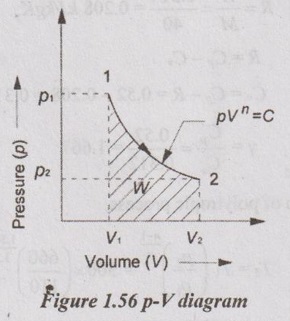
Case 1: Ethane

Case 2: Argon

AU Problem 1.22

Determine the heat transfer and its direction for a system in which a perfect gas having molecular weight of 17.76 is compressed from 101.3 kPa, 20°C to a pressure of 600 kPa following the law pV1.3 = constant. Take specific heat at constant pressure of gas as 1.7 kJ/kgK.

Given data:

M = 17.76

p1 = 101.3 kPa

T1 = 20°C = 20 + 273 = 293 K

p2 = 600 kPa

n = 1.3

Cp =1.7 kJ/kgK

To find:

Q and its direction

Solution:

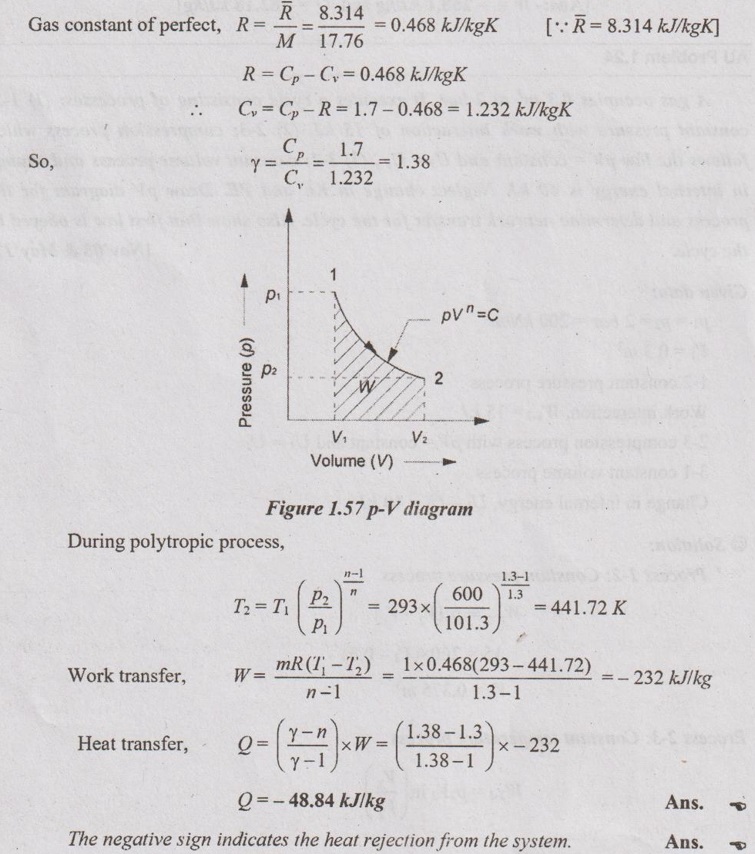
AU Problem 1.23

Determine the work transfer and heat transfer for a system in which a perfect gas having molecular weight of 16 kg/kmol is compressed from 101.3 kPa, 20°C to a pressure of 600 kPa following the law pV1.3 = constant. Take specific heat at constant pressure of gas as 1.7 kJ/kgK.

Similar to AU Problem 1.22 on Page 1.116.

[Ans:- W = -258.1 kJ/kg and Q = -82.18 kJ/kg]

AU Problem 1.24

A gas occupies 0.3 m3 at 2 bar. It executes a cycle consisting of processes: (1) 1-2; constant pressure with work interaction of 15 kJ, (2) 2-3; compression process which follows the law pV = constant and U3 = U2, (3) 3-1; constant volume process and change in internal energy is 40 kJ. Neglect change in KE and PE. Draw pV diagram for the process and determine network transfer for the cycle. Also show that first law is obeyed by the cycle. 

Given data:

p1 = p2 = 2 bar = 200 kN/m2

V1 = 0.3 m3

1-2 constant pressure process

Work interaction, W1-2 = 15 kJ

2-3 compression process with pV = constant and U3 = U2

3-1 constant volume process

Change in internal energy, U1 - U3 = 40 kJ

Solution:

Process 1-2: Constant pressure process

W1-2 = p1(V2 - V1)

15 = 200 × (V2 - 0.3)

⸫ V2 = 0.375 m3

Process 2-3: Constant temperature process

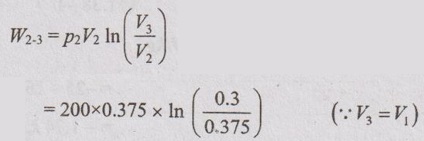
W2-3 = -16.74 kJ

Change in internal energy, ΔU = U3 - U2 = 0 for isothermal process.

⸫ Heat transfer, Q2-3 = Work transfer, W2-3 = -16.74 kJ

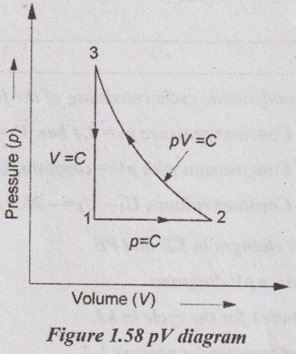
Process 3-1: Constant volume process

V1 = V3 = 0.375m3

Work transfer, W3-1 = 0

⸫ Heat transfer. Q3-1 = ΔU = 40 kJ

Network of the cycle, Wnet = W1-2 + W2-3 + W3-1

= 15 - 16.74 + 0 = -1.74 kJ   Ans.

Internal energy for process 1-2,

U1-2 = U2 - U1

= (U2 – U3) + (U3 – U1)

= (U2 – U3) + (U3 – U1)

= 0 + (-40) = -40 kJ

⸫ Heat transfer, Q1-2 = W1-2 + U1-2 = 15 – 40 = -25 kJ

Net heat transfer of the cycle,

Qnet = Q1-2 + Q2-3 + Q3-1

= -25 -16.74 + 40

= -1.74 kJ = Network of the cycle, Wnet

As per the first law of thermodynamics, net work transfer is equal to the net

heat transfer i.e. ΣQcycle = ΣWcycle. In this problem, Wnet = Qnet.

Hence, ΣQcycle = ΣWcycle proved.   Ans.

AU Problem 1.25

A gas undergoes a thermodynamic cycle consisting of the following processes:

(i) Process 1-2: Constant pressure pi = 1.4 bar, V1 = 0.028 m3, W12 = 10.5 kJ.

(ii) Process 2-3: Compression with pV= constant, U3 = U2.

(iii) Process 3-1: Constant volume, U1 - U3 = -26.4 kJ.

There are no significant changes in KE and PE

(1) Sketch the cycle on a pV diagram.

(2) Calculate the network for the cycle in kJ. 

(3) Calculate the heat transfer for process 1-2. 

(4) Show that ΣQcycle = ΣWcycle.

Similar to AU Problem 1.24 on Page 1.118.

[Ans:- Network of the cycle, Wnet = -8.28 kJ and heat transfer, Q1-2 = 36.9 kJ]

AU Problem 1.26

A three process cycle operating with nitrogen as the working substance has constant temperature compression at 34°C with initial pressure 100 kPa. Then the gas undergoes a constant volume heating and then polytropic expansion with 1.35 as index of compression. The isothermal compression requires - 67 kJ/kg of work.

Determine:

(i) p, v and T around the cycle

(ii) Heat in and out

(iii) Net work.

For nitrogen gas, Cv = 0.731 kJ/kgK.

Given data:

T1 = 34°C = 273 + 34 = 307 K = T2

p1 = 100 kPa

W1-2 = -67 kJ/kg

Process 1-2 is constant temperature (compression)

Process 2-3 is constant volume (heat addition)

Process 3-1 is polytropic (expansion)

For nitrogen, Cv = 0.731 kJ/kgK

To find:

Pressure and temperature at all points, heat in, heat out and net work.

Solution:

Molecular weight of nitrogen, N2 = 2 × 14 = 28 kg/kmol

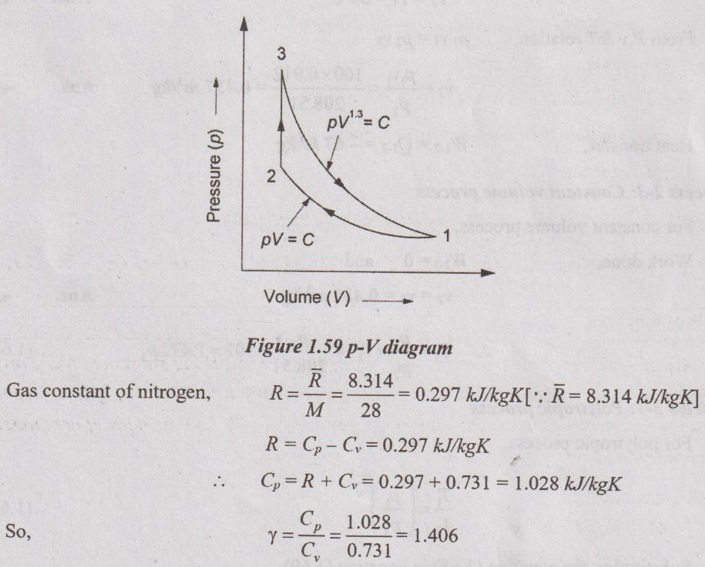
From characteristic gas equation,

P1V1 = R T1

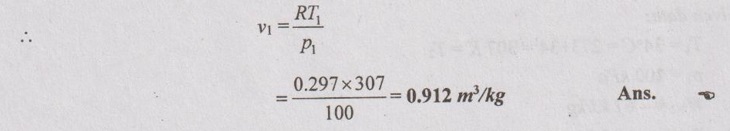
Process 1-2: Constant temperature process

For constant temperature process,

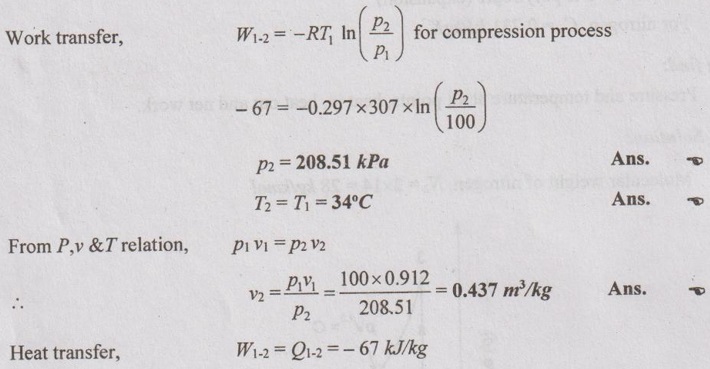
Process 2-3: Constant volume process

For constant volume process,

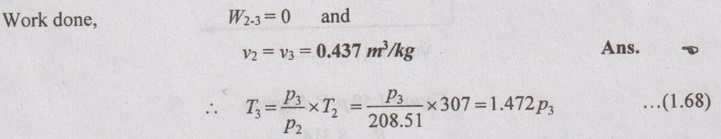
Process 3-1: Polytropic process

For polytropic process,

Substituting the equation (1.68) in equation (1.69),

AU Problem 1.27

Three grams of nitrogen gas at 6 atm and 160°C in a frictionless piston cylinder device is expanded adiabatically to double its initial volume, then compressed at constant pressure to its initial volume and then compressed again at constant volume to its initial state. Calculate the net work done on the gas. Draw the p-V diagram for the processes. 

Given data:

m = 3g = 0.003 kg

p1 = 6 atm = 6 × 1.0132 = 6.0792 bar  [since, 1 atm = 1.0132 bar & 1 bar = 100 kPa]

= 6.0792 × 100 = 607.92 kPa

T1 =160°C = 273 + 160 = 433 K

Process 1-2 is adiabatic expansion (V2 = 2V1)

Process 2-3 is constant pressure compression (p2 = p3 and V3 = V1)

 Process 3 - 1 is constant volume compression (V3 = V1)

To find:

Net work done

Solution:

Molecular weight of nitrogen, N2 = 2 × 14 = 28 kg/kmol

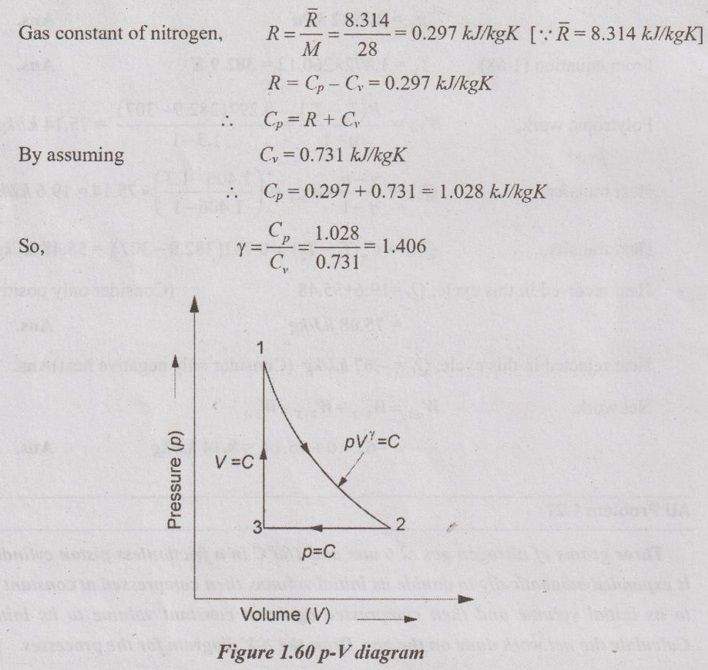
Process 1-2: Adiabatic expansion process

From the relations of adiabatic expansion process,

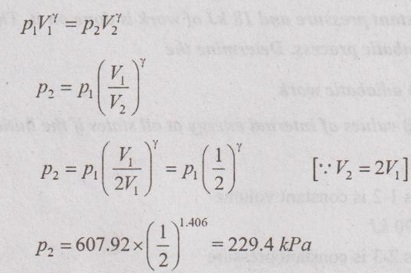
From ideal gas equation,

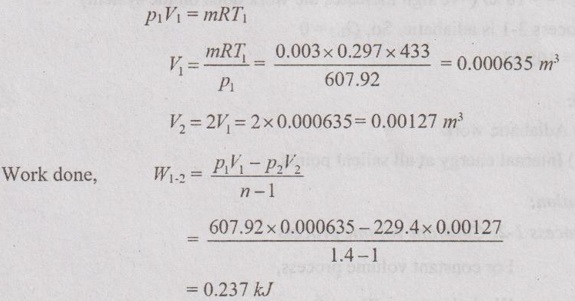
Process 2-3: Constant pressure process

For constant pressure process, 

Work done, W2-3 = p2 (V3 - V2)

= 229.4 × (0.000635 - 0.00127)   [⸪ V3 = V1]

= 0.147 kJ

Process 3-1: Constant volume process

For constant volume process,

Work done, W3-1 = 0

Net work, Wnet = W1-2 + W2-3 + W3-1

= 0.237 - 0.147 + 0 = 0.09 kJ       Ans.

AU Problem 1.28

90 kJ of heat is supplied to a system at a constant volume. The system rejects 95 kJ of heat at constant pressure and 18 kJ of work is done on it. The system is brought to original state by adiabatic process. Determine the

(i) adiabatic work

(ii) values of internal energy at all states if the initial value is 105 kJ. 

Given data:

Process 1-2 is constant volume

Q1-2 = 90 kJ

Process 2-3 is constant pressure

Q2-3 = -95 kJ (-ve sign indicates the heat rejection)

W2-3 = -18 kJ (-ve sign indicates the work done on the system)

Process 3-1 is adiabatic. So, Q2-3 = 0

U1 = 105 kJ

To find:

(i) Adiabatic work

(ii) Internal energy at all salient points.

Solution:

Process 1-2: Constant volume process

For constant volume process,

Work done, W1-2 = 0

Based on first law of thermodynamics,

Heat suuply, Q1-2 = W1-2 + ΔU1-2

90 = 0 + ΔU1-2

⸫ ΔU1-2 = 90 kJ

But, ΔU1-2 = U2 - U1

90 = U2 - 105

⸫ U2 = 195 kJ      Ans.

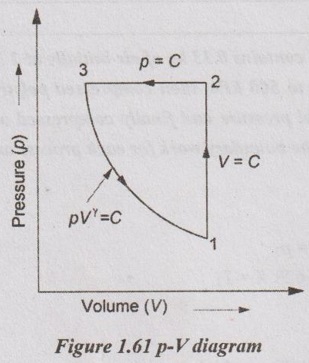
Process 2-3: Constant pressure process

For constant pressure process,

Q2-3 = -95 kJ

W2-3 = -18 kJ

Based on first law of thermodynamics,

Heat done, Q2-3 = W2-3 + ΔU2-3

-95 = -18 + ΔU2-3

⸫ ΔU2-3 = -95 + 18 = -77 kJ

But,  ΔU2-3 = U3 - U2

-77 = U3 - 195

⸫ U3 = 195 - 77 = 118 kJ   Ans.

Process 3-1: Adiabatic process

For adiabatic process,

Q2-3 = 0

From first law of thermodynamics for cyclic process,

Q1-2 + Q2-3 + Q3-1 = W1-2 + W2-3 + W3-1

90 – 95 + 0 = 0 – 18 + W3-1

Adiabatic work, W3-1 = 13 kJ    Ans.

AU Problem 1.29

A piston-cylinder device contains 0.15 kg of air initially at 2 MPa and 350°C. The air is first expanded isothermally to 500 kPa, then compressed polytropically with a polytropic exponent of 1.2 to the initial pressure and finally compressed at the constant pressure to the initial state. Determine the boundary work for each process and network of the cycle.

Given data:

m = 0.15 kg

p1 = 2 MPa = 2000 kPa = p3

T1 = 350°C = 273 + 350 = 623 K = T2

p2 = 500 kPa

n = 1.2

Process 1-2 is isothermal (Expansion)

Process 2-3 is polytropic (Compression)

Process 3-1 is constant pressure (Compression)

Solution:

Process 1-2: Isothermal expansion process

Process 2-3: Polytropic compression process

For polytropic process,

p2V2n – p3V3n

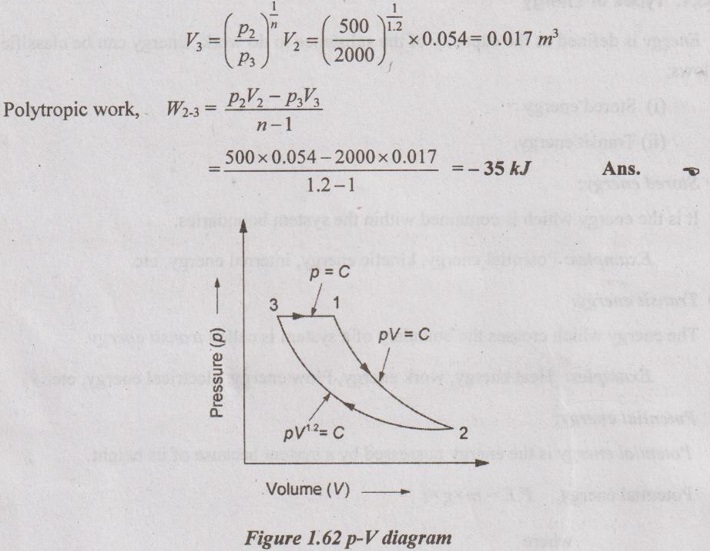
Process 3-1: Constant pressure process

For constant pressure process, 

Work done, W3-1 = p3(V1 - V3)

= 2000 (0.0134 - 0.017) = -7.2 kJ          Ans.

Net work, Wnet = W1-2 + W2-3 + W3-1

= 37.18 – 35 - 7.2 = -5.02 kJ       Ans.