Solved Anna University Problems on closed systems (cyclic process): Basics, Zeroth and First Law - Engineering Thermodynamics
SOLVED ANNA UNIVERSITY PROBLEMS ON CLOSED SYSTEMS (CYCLIC PROCESS)
AU Problem 1.1
A gas whose original pressure, volume and temperature were 140 kN/m3, 0.1 m3 and 25°C respectively is compressed such that new pressure is 700 kN/m2 and its new temperature is 60°C. Determine the new volume of the gas.
Given data:
P1 = 140 kN/m2
V1 = 0.1 m3
T1 = 25°C = 25 + 273 = 298 K
p2 = 700 kN/m2
T2 = 60°C = 60 + 273 = 333 K
To find:
V2
Solution:
From ideal gas equation,

AU Problem 1.2
During the working stroke of an engine the heat transferred out of the system was 150 kJ/kg of the working substance. Determine the work done when the internal energy is decreased by 400 kJ/kg. Also state whether the work done on or by the engine.
Given data:
Q = -150 kJ/kg ('-' sign is due to the heat transferred out of the system)
ΔU = -400 kJ/kg (('-' sign is due to the decrease in internal energy)
To find:
Work done, W
Solution:
By first law of thermodynamics,
Q = W +ΔU
⸫ W = Q – ΔU = -150 - (-400) = 250 kJ/kg Ans.![]()
(Positive work indicates that the work done is by the engine.)
AU Problem 1.3
Define a new thermodynamic scale say degree No, in which the freezing point and boiling point of water are 100°N and 300°N respectively. Correlate this temperature scale with centigrade scale.
New temperature scale is defined as the temperature of any system is a property which determines whether the system is in thermal equilibrium with other systems or not.
Temperature of boiling point of water, θ(X1) = 300°N
Temperature of freezing of water, θ (X2) = 100°N
Two fixed points on centigrade scale = 100°C

So, the same value of temperature on centigrade is taken on the new thermodynamic scale.
AU Problem 1.4
A rigid tank containing 0.4 m3 of air at 400 kPa and 30°C is connected by a valve to a piston cylinder device with zero clearance. The mass of the piston is such that a pressure of 200 kPa is required to raise the piston. The valve is opened slightly and air is allowed to flow into the cylinder until the pressure of the tank drops to 200 kPa. During this process, the heat is exchanged with the surrounding such that the entire air remains at 30°C at all times. Determine the heat transfer for this process.
Given data:
Volume, V1 = 0.4 m3
Pressure, p1 = 400 kPa
Temperature, T1 = 30°C
Pressure, p2 = 200 kPa
Temperature, T2 = 30°C
Solution:
The rigid tank is considered as a closed system. Therefore, the change in internal energy due to constant temperature throughout the process is zero.
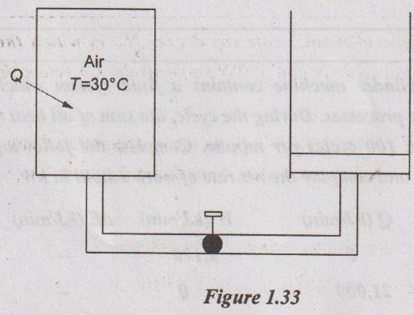
As per the first law of thermodynamics,
Q = W + ΔU
For closed system, ΔU = 0
Q = W
From ideal gas equation,
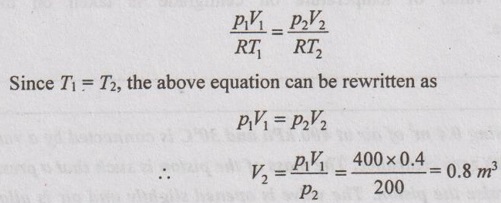
Work done at the boundary, W = p2 (V2 - V1) = 200 (0.8-0.4) = 80 kJ
We know that the heat transfer to the surrounding, Q = W
⸫ Q = 80 kJ Ans.![]()
AU Problem 1.5
25 people attended a farewell party in a small room of size 10 × 8 m and have a 5 m ceiling. Each person gives up 350 kJ of heat per hour. Assuming that the room is completely sealed off and insulated, calculate the air temperature rise occurring in 10 minutes. Assume Cv of air 0.718 kJ/kgK and R = 0.287 kJ/kg K and each person occupies a volume of 0.005 m3. Take p = 101.325 kPa and T = 20°C.
Same as Problem 1.11 on Page 1.54.
AU Problem 1.6
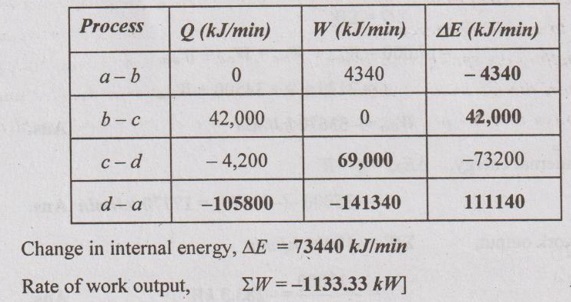
A piston and cylinder machine contains a fluid system which passes through a complete cycle of four processes. During the cycle, the sum of all heat transfers is - 170 kJ. The system completes 100 cycles per minute. Complete the following table showing the method for each item and compute the net rate of work output in kW.
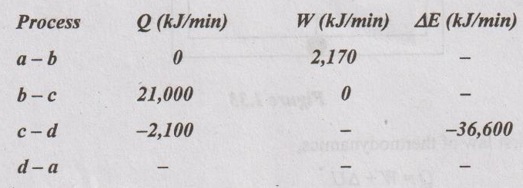
Solution:
Process a - b:
By first law of thermodynamics,
Q = W + ΔE
0 = 2170 + ΔE
ΔE = -2170 kJ/min
Process b-c:
Q = W + ΔE
21,000 = 0 + ΔE
ΔE = 21,000 kJ/min
Process c-d:
-2,100 = W - 36,600
W = 34,500 kJ/min
Process d-a:
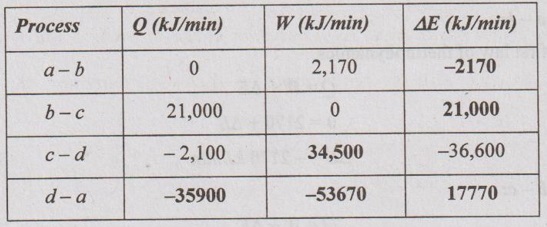
ΣQ = -170 kJ (given)
Number of cycles/min = 100
The total heat transfer, Σcycle Q = -170 × 100 = 17,000 kJ/min
Σcycle Q = Qa-b + Qb-c + Qc-d + Qd-a
- 17,000 = 0 + 21000 2100 + Qd-a
Qd-a = - 35900 kJ/min Ans.![]()
In a cyclic process,
ΣQ = ΣW
-17,000 = Wa-b + Wb-c + Wc-d + Wd-a
= 2170 + 0 + 34500 + Wd-a
Wd-a = -53670 kJ/min Ans. ![]()
Change in internal energy, ΔEd-a = Q - W
= -35900 - (-53670) = 17770 kJ/min Ans.![]()
⸫ Rate of work output, ΣW = -17000 kJ/min
= -17000 / 60 = -283.3 kW Ans.![]()
Result:
AU Problem 1.7
A fluid system contained in a piston and cylinder machine passes through a complete cycle of four processes. The sum of all heat transferred during a cycle is - 340 kJ. The system completes 200 cycles per min.

Complete the above table showing the method for each item and compute the net rate of work output in kW.
Similar to AU Problem 1.6 on Page 1.58.
AU Problem 1.8
A Van der Waals gas is compressed reversibly at constant temperature from volume V1 to V2. The equation of state is given by mole by p = 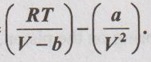 Determine the work done per mole of the gas.
Determine the work done per mole of the gas.
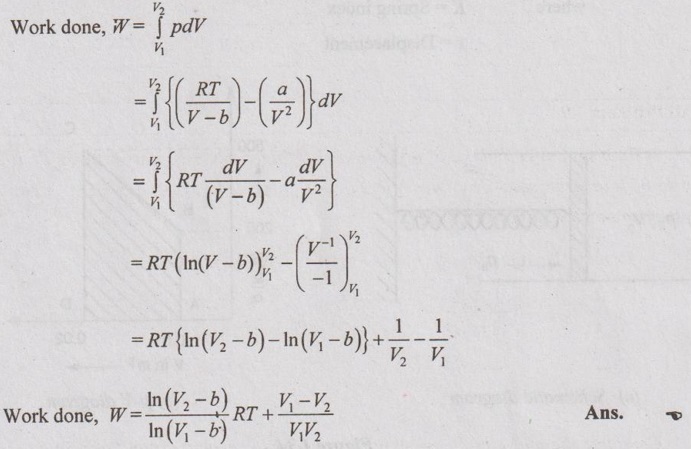
AU Problem 1.9
A piston cylinder assembly contains air (ideal gas with γ = 1.4) at 200 kPa and occupies a volume of 0.01 m3. The piston is attached to one end of a spring and the other end of the spring is fixed to a wall. The force exerted by a spring on the piston is proportional to the decrease in length of the spring from its natural length. The ambient atmospheric pressure is 100 kPa. Now, the air in the cylinder is heated till the volume is doubled and at this instant, it is found that the pressure of the air in the cylinder is 500 kPa. Calculate the work done by the gas.
Given data:
γ = 1.4
p1 = 200 kPa
V1 = 0.01 m3
po = 100 kPa
V2 = 2V1
p2 = 500 kPa
Solution:
Force exerted by the spring on the piston,
Fs = K(x - xo)
where K = Spring index
x = Displacement
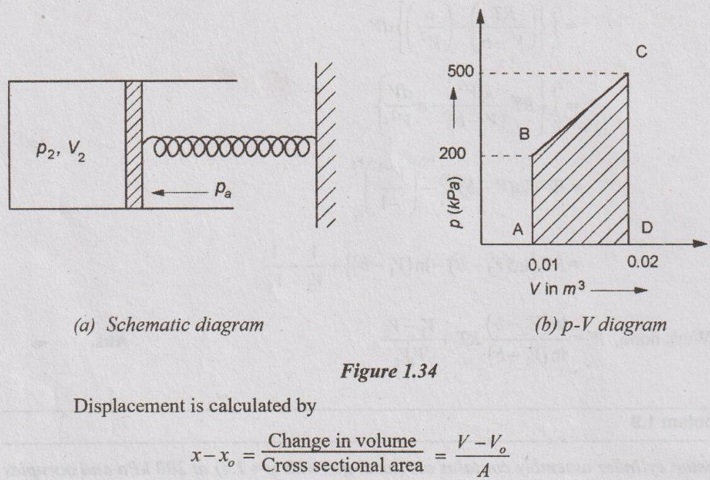
where
V = Volume of air in the cylinder if the spring is compressed by displacement x
Vo = Volume of air in the cylinder if the spring is at its natural length
Then force acting on the piston due to ambient atmosphere,
F = poA [ ⸪ Force = Pressure × Area]
⸫ Force balance on the piston for the air volume, V
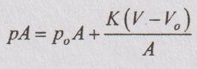
Dividing by A on both sides,

The piston will move from initial state 1 to final state 2 when the air is heated.
⸫ Force balance for the initial state,

We know that the mechanical work done by the air is calculated by

AU Problem 1.10
A system receives 200 kJ of energy as heat, at constant volume. Then it is cooled at constant pressure when 50 kJ of work was done on the system while it rejects 70 kJ of heat. Supposing the system is restored to the initial state by an adiabatic process, how much work will be done by the system?
Given data:
Q1-2 = 200 kJ
W1-2 = 0 for constant volume process
W2-3 = -50 kJ
Q2-3 = -70 kJ
Q3-1 = 0 for adiabatic process
To find:
Work done by the system, W
Solution:
From first law of thermodynamics,
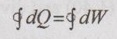
For constant volume process, W1-2 = 0
For adiabatic process, Q3-1 = 0
Q1-2 + Q2-3 + Q3-1 = W1-2 + W2-3 + W3-1
200 – 70 + 0 = 0 – 50 + W3-1
W3-1 = 180 kJ
Work done by the system,
W = W1-2 + W2-3 + W3-1
= 0 – 50 +180 = 130 kJ Ans.![]()
AU Problem 1.11
A piston and cylinder machine containing a fluid system has a stirring device as shown in Figure 1.35.
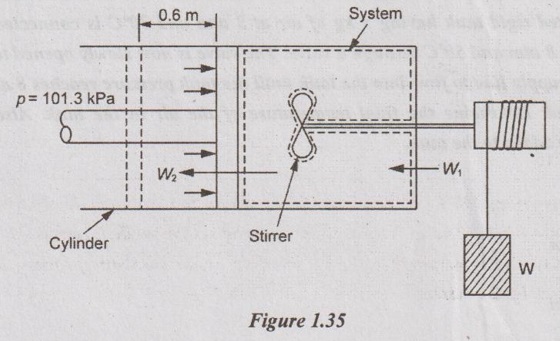
The piston is frictionless, and it is held down against the fluid due to atmospheric pressure of 101.3 kPa. The stirring device is turned 9500 revolutions with an average torque against the fluid of 1.25 Nm. Meanwhile the piston of 0.65 m diameter moves out 0.6 m. Find the network transfer for the system.
Given data:
p =101.3 kPa
N = 9500 rev.
T = 1.25 Nm
Dp = 0.65 m
Lp = 0.6 m
Solution:
Work done by the stirring device upon the system,
W1 = 2πNT = 2 × π × 9500 × 1.25 = 74612.8 Nm or J = 74.6 kJ
This is negative work as it is done upon the system.
Work done by the system upon the surroundings,
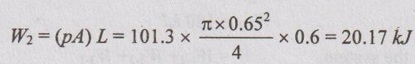
This is a positive work as it is done by the system.
Therefore, net work transfer for the system,
AU Problem 1.12
W = W1 + W2 = -74.6 + 20.17 = -54.43 kJ Ans.![]()
AU Problem 1.12
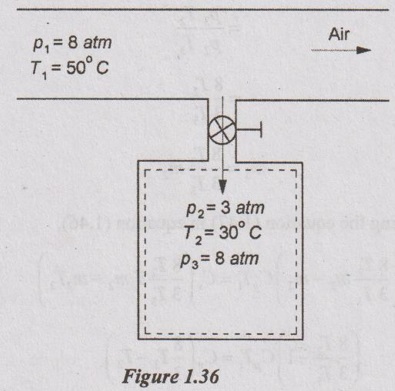
An insulated rigid tank having 5 kg of air at 3 atm and 30°C is connected to an air supply line at 8 atm and 50°C through a valve. The valve is now slowly opened to allow the air from the supply line to flow into the tank until the tank pressure reaches 8 atm and the valve is closed. Determine the final temperature of the air in the tank. Also, find the amount of air added to the tank.
Given data:
m = 5 kg
p1 = 8 atm
T1 = 50°C
p2 = 3 atm
T2 = 30°C
p3 = 8 atm
Solution:
As per conservation of mass,
Mass of air supplied to the tank = Final mass of air in the tank - Initial mass of air in the tank
So, m1 = m3 - m2 ... (1.43)
As per first law of thermodynamics,
Q = W + ΔU
Q = 0 for insulated tank and
W = 0 for rigid tank
⸫ ΔU = 0
So, it is inferred that the energy associated with air inside the tank takes place at constant volume.
As per conservation of energy,
Energy entering the tank = Final energy - Initial energy
m1h1 = m3u3 - m2u2 ... (1.44)
The above equation (1.44) can be written as
m1CpT1 = m3CvT3 - m2CvT2 ... (1.45)
Substituting the equation (1.43) in equation (1.45),
(m3 - m2)CpT1 = Cv (m3T3 - m2T2) ... (1.46)
We know that the ideal gas equation can be written as
pV = mRT
From ideal gas equation, mass can be calculated by
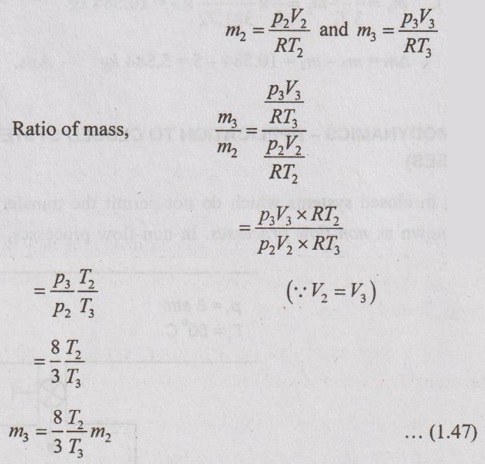
Substituting the equation (1.47) in equation (1.46),
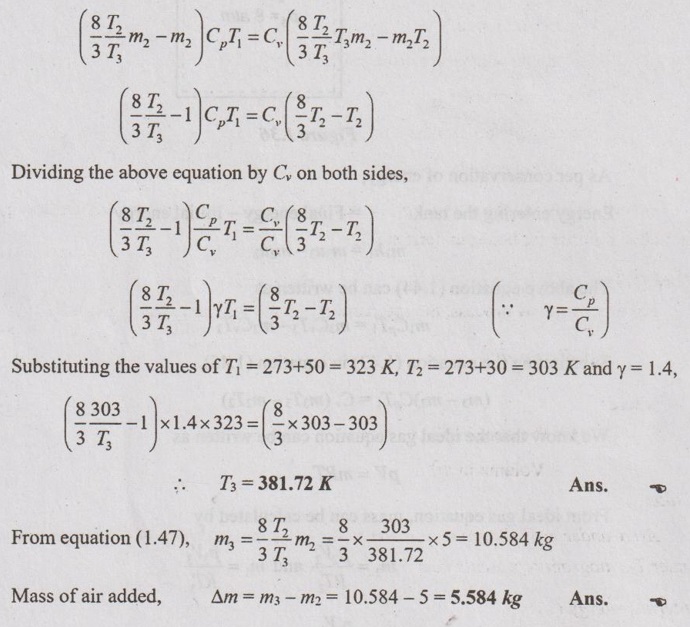
No comments:
Post a Comment