Problem - 1
A crude oil of viscosity 0.9 poise and relative density 0.9 is flowing through a horizontal circular pipe of diameter 120 mm and length 12 m. Calculate the difference of pressure at the two ends of the pipe. If 785 N of the oil is collected in a tank in 25 seconds.
Given data:
Viscosity (μ) = 0.9 poise 0.09 N - s/m2
Relative density (or) specific gravity (S) = 0.9
Pipe diameter (D) = 120mm == 0.12m
Length of pipe (L) = 12m
Weight of oil (w) = 785 N
Time to collect oil in the tank (t) = 25 sec
To find:
Calculate the difference in pressure (p1 - p2)
Solution:
(iv) Discharge (Q) = A × V
Hence the flow is laminar
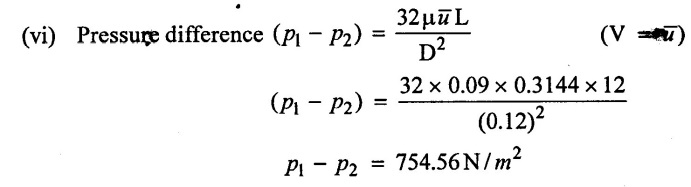
Result:
Pressure difference (p1 – p2) = 754.56N/m2
Problem - 2
An oil specific gravity 0.9 and viscosity 0.06 poise in flowing through a pipe of diameter 200 mm at the rate of 60 lit/sec. Find the head loss due to friction for a 500 m length of the pipe. Find the power required to maintain this flow.
This problem is similar to Example No-48, page No-2.131.
Ans:
(i) Loss of head (hf) = 9.48 m of water
(ii) Power required (p) = 5.02 Kw
Problem - 3
A laminar flow is taking place in pipe of diameter 20 cm. The maximum velocity is 1.5 m/s. Find the mean velocity and radius at which this occurs. Also calculate the velocity at 4 cm from the wall at pipe.
This problem is similar to Example No - 6, page No-2.17.
Ans:
(i) Mean velocity occurs at radius (r) = 0.0707 m
(ii) Velocity at the distance 0.04 m (u) = 0.96 m/s
Problem - 4
An oil of specific gravity 0.7 is flowing through a pipe of diameter 30 cm at the rate of 500 lit/sec. Find the head lost due to friction and power required to maintain the flow for a length at 100 m. Take v = 0.29 stokes.
This problem is similar to Example No - 48, page No-2.131.
Ans:
(i) Loss of head due to friction (hf) = 163.23 m
(ii) Power required (p) = 560.5Kw
Problem - 5
For a turbulent flow in a pipe of diameter 300 mm. Find the distance when the centre line velocity is 0.2 m/s and the velocity at a point 100 mm from the centre as measured by pilot tube is 1.6 m/s.
Given data:
Pipe diameter (D) = 300 mm = 0.3m
Centre line velocity (Umax) = 2.0m/s
Velocity at a point 100 mm (u) = 1.6m/s
To find:
Discharge (Q)
Solution:
(i) Universal velocity distribution equation for turbulent flow in pipes is
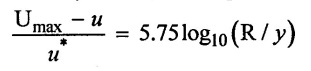
Where
Maximum velocity (Umax) = 2m/s
Local velocity (u) = 1.6m/s
(ii) Velocity distribution for a rough pipe
Result:
Discharge (Q) = 0.1027 m3/s
Problem - 6
A pipe of 10 cm in diameter and 100 m long is used to pump oil and viscosity 8.5 poise and specific gravity 0.92 at the rate of 1200 U/min. The first 30 m of pipe upwards 10° to 15° horizontal. Determine the pressure required to be developed by the pump and the power required to driving motor if pump efficient is 60%.
Given data:
Diameter for pipe (D) = 10cm = 0.1m
Length (L) = 1000 m
Viscosity (μ) = 8.5 poise = 0.85N - s /m2
Specific gravity of oil (S) = 0.92
Discharge (Q) 1200 lit/min = 20 × 10-3 m3/sec
Pump efficiency (η) = 60% = 0.6
To find:
(i) Pressure difference (p1 – p2)
(ii) Power required (p)
Solution:
Result:
(i) Pressure difference (p1 – p2) = 2.3358 × 106 N/m2
(ii) Power required (p) = 28.02 Kw
Problem - 7
A lubricating oil flows in a 10 cm diameter pipe at 1 m/s. Determine whether flow is laminar (or) turbulent. For lubricating oil μ = 0.1N-s/m2 and 930Kg/m3. Calculate also transition and turbulent velocities.
Given data:
Pipe diameter (D) = 10 cm = 0.1m
Velocity (V) = 1m/s
Viscosity (μ) = 0.1N – s/m2
Density (ρ) = 930 Kg/m3..
To find:
(i) Type of flow laminar (or) turbulent
(ii) Transition and turbulent velocity
Solution:
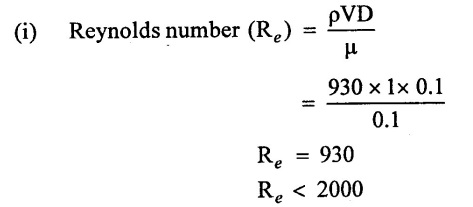
Hence the flow is laminar
(ii) Transition flow is a mixture of both laminar and turbulent flow, with turbulence at centre of pipe and laminar near edges.
Here the given flow in laminar, so transition and turbulent velocities does not occur.
Result:
(i) Type of flow is laminar Re < 2000
(ii) Transition and turbulent velocities are not occur
Problem - 8
A pipe line 20 cm in diameter 70 m long, conveys oil of specific gravity 0.95 and viscosity 0.23N-s/m2. If the velocity of oil is 1.38 m/s. Find the difference in pressure between the two ends of the pipe.
Given data:
Length of pipe (L) = 70 cm
Diameter (D) = 20 cm = 0.2m
Specific gravity (S) = 0.95
Viscosity (μ) = 0.23N - s/m2
Velocity (V) = 1.38m/s
To find:
Pressure difference (p1 − p2)
Solution:
Re = 1140
Re < 2000, Hence this is laminar flow.
(ii) Using Hagen Poiseuille equation
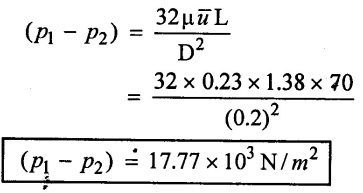
Result:
Pressure difference (p1 − p2) = 17.77 × 103 N/m2
Problem - 9
For a turbulent flow in a pipe of diameter 300 mm, find discharge when the centre line velocity is 2.0 m/s and the velocity at a point 100 mm from the centre as measured by pitot tube is 1.6 m/s.
This problem is same as university solved problem No - 5, page No-271
Ans:
Discharge Q) = 0.1027 m3 / s
Problem - 10
A Pipe of 12 cm diameter is carrying an oil (μ = 2.2 pas and p = 1250 Kg/m3) with a velocity of 4.5 m/s. Determine the shear stress at the wall surface of the pipe, head loss, if the length of the pipe is 25 m and the power lost.
Given data:
Diameter (D) = 12 cm = 0.12m
Viscosity (μ) = 2.2 pas = 2.2 N-s/m2
Density (ρ) = 1250 Kg/m3
Velocity (v) = 4.5 m/s
Length (L) = 25m
To find:
(i) Shear stress (τ)
(ii) Head loss (hL)
(iii) Power lost (p)
Solution:
Result:
(i) Shear stress (τ) = 660N/m2
(ii) Power lost (p) = 28.048 watts
Problem - 11
Oil with a density of 900 kg/m3 and kinematic viscosity of 6.2 × 10-4 m2/s is being discharged by a 6 mm diameter, 40 m long horizontal pipe from a storage tank open to the atmosphere. The height of the liquid level above the center of the pipe is 3m. Neglecting the minor losses, determine the flow rate of oil through the pipe.
Given data:
Density (ρ) = 900 Kg/m3
Kinematic viscosity (v) = 6.2 × 10-4 m2/s
Diameter (D) = 6mm = 0.006m
Length (L) = 40m
Height (or) head (h) = 3m
To find:
Discharge (Q)
Solution:
Result:
Discharge (Q) = 3.78 × 10-8 m3 / sec
Problem - 12
A 20 cm diameter pipe 30 Km long transports oil from a tanker to the store at 0.01 m3/s. Find Reynolds number to classify the flow. Take viscosity m = 0.1 N-s/m2 and density ρ = 900Kg/m3 for oil.
This problem is similar to university solved problem No-7, page No-2.214.
Ans:
Reynolds number Re = 85.86 × 106 > 2000, so the flow in turbulent flow.
Problem - 13
Two tanks of fluid (p = 998 Kg/m3 and μ = 0.001 Kg / ms ) at 20° C are connected by a capillary tube 4 mm in diameter and 3.5 m long. The surface of the tank 1 is 30 cm higher than the surface of tank 2. Estimate the flow rate in m3/hr. Is the flow is laminar? For what tube diameter will Reynolds number be 500?
Given data:
Density (ρ) = 998Kg/m3
Dynamic viscosity (μ) = 0.001 Kg/m.s = 0.001 N - s/m2
Capillary tube diameter (D) = 4mm = 0.004 m
Length (L) = 3.5m
Datum difference (h) = 30m = 0.3m
To find:
(i) Discharge (Q)
(ii) Check the type of flow
(iii) Tube diameter when Re = 500
Solution:
(i) According to Hagen-Poiseuilli's equations, we have
(ii) W.K.T Discharge is
Q = A × V
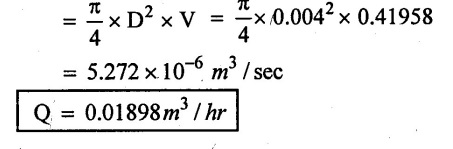
(iii) Reynolds number (Re) = ρVD / μ
Hence this is laminar flow
(iv) Diameter of tube, when Re = 500
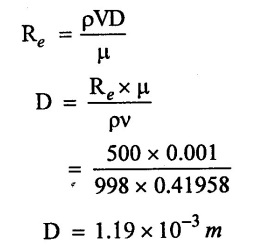
Result:
(i) Discharge (Q) = 0.01898 m3 / hr
(ii) Flow in laminar (Re < 2000)
(iii) Diameter of tube when Re = 500 = 1.19mm
Problem - 14
For the velocity profile in laminar boundary layer as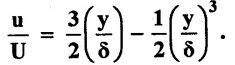 
Find the thickness of the boundary layer and shear stress 1.8 m from the leading edge of a plate. The plate is 2.5 m long and 15 m wide is placed in water, which is moving with a velocity of 15 cm/sec. Find the drag on one side of the plate if the viscosity of water is 0.01 poise.
This problem is similar to Example No-28, page No-2.78.
Ans:
δ = 0.016m, τo = 0.014N/m2, FD = 0.08N
Problem - 15
Air is flowing over flat plate with a velocity of 5 m/s. The length of the plate is 1.5 m and width1 m. The kinematic viscosity of air is given as 0.158 × 10-4 m2/s. Find
(i) The boundary layer thickness at end of the plate
(ii) The shear stress at 20 cm from the leading edge
(iii) Drag force on the side of the plate. Take the velocity over a plate as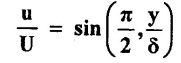 
and the density of air is 1.24 Kg/m3.
This problem is similar to Example No-27, page No-2.76.
Ans:
δ = 0.01044 m, FD = 0.0442N, τo = 0.0403 N/m2
Problem - 16
A smooth two dimensional flat plate is expected to a wind velocity of 100 Km/hr. If laminar boundary layer exists up to the value of (Re)x equal to 3 × 105. Find the maximum distance up to which laminar boundary layer exists and find its maximum thickness. Assume kinematic viscosity of air as 1.49 × 10-5 m2/s
Given data:
Velocity (v) = 100Km/hr = 
Reynolds number (Re) = 3 × 105
Kinematic viscosity (v). = 1.49 × 10-5 m2 / s
To find:
(i) Laminar flow distance exists
(ii) Laminar flow thickness maximum up to (Re) = 5 × 105
Solution:
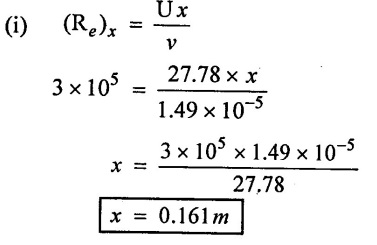
(ii) Maximum thickness when maximum limit of Reynolds number
Result:
(i) Exist boundary layer distance (x) = 0.16m
(ii) Maximum boundary layer thickness (L) = 0.268 m
Problem - 17
A flat plate 1.5 m × 1.5 m moves at 50 Km/hr in a stationary air of density 1.15 Kg/m3. If the co-efficient of drag and lift are 0.15 and 0.75 respectively. Determine (i) The lift force (ii) The drag force (iii) The resultant force and power required to set the plate in motion.
Given data:
Area of the plate (A) = 1.5 × 1.5 = 2.25 m2
Velocity (V) = 50Km/hr = 50 × 1000 / 3600 = 13.89m/s
Co-efficient of drag (CD) 0.15
Co-efficient of lift (CL) = 0.75
Density of air (ρ) = 1.15Kg/m3
To find:
(i) Lift force (FL)
(ii) Drag force (FD)
(iii) Resultant force (FR)
(iv) Power required (p)
Solution:
Result:
(i) Lift force (FL) = 182.21N
(ii) Drag force (FD) = 37.44 N
(iii) Resultant force (FR) = 190.92N
(iv) power (p) = 2.65Kw
Problem - 18
A smooth flat plate with in sharp leading edge is placed along a free stream of water flowing at 3 m/s. Calculate the distance from the leading edge and the boundary thickness where the transition from laminar to turbulent flow may commence. Assume the density of water as 1000Kg/m3 and viscosity as 1 centi poise.
Given data:
Free stream Velocity (U) = 3m/s
Density (ρ) = 1000Kg/m3
Viscosity (μ) = 1centi poise = 1 × 10-2 poise = 1 × 10-3 N – s/m2
To find:
(i) Laminar flow distance from leading edge
(ii) Boundary layer thickness (δ)
Solution:
Result:
(i) Laminar flow distance (x) = 0.166 m
(ii) Boundary layer thickness (δ) = 1.178 × 10−3 m
Problem - 19
A plate of 600 mm length and 400 mm wide is immersed in a fluid of specific gravity 0.9 and kinematic viscosity (v) 10-4 m2/s. The fluid in moving with the velocity of 6 m/s. Determine
(i) Boundary layer thickness
(ii) Shear stress at the at the end of the plate
(iii) Drag force on one side of the plate
Given data:
Length (L) = 600mm = 0.6m
Width (b) = 400 mm = 0.4m
Specific gravity (S) = 0.9
Kinematic viscosity (v) = 1 × 10-4 m2 / s
Velocity (U) = 6m/s
To find:
(i) Boundary layer thickness (δ)
(ii) Shear stress at the end of the plate (τo)
(iii) Drag force on one side of the plate (FD)
Solution:
This problem is not having any velocity profile so, that Blasius's solution will be used
Result:
(i) Boundary layer thickness (δ) = 0.0158m
(ii) Shear stress at end of plate (τo) = 56.693 N
(iii) Drag force of one side of the plate (FD) = 27.21N
Problem - 20
Compare the rate of growth of the laminar boundary layer over a smooth flat plate in the following cases.
(i) Flat plate placed in a water stream flowing at 2 m/s
(ii) Flat plate in an air stream flowing at 2 m/s
(iii) Flat plate placed in an air stream flowing at 8 m/s.
Then density of water and air are 1000 kg/m3 and 1.2Kg/m3 respectively and the viscosity of water and air are 0.001 and 0.00019N-s/m2 respectively.
Given data:
Density of water (ρw) = 1000 Kg/m3
Density of air (ρa) = 1.2Kg/m3
Viscosity of water (μw) = 0.001N-s/m2
Viscosity of air (μa) = 0.00019N-s/m2
To find:
Compare the growth of boundary layer
Solution:
Flat plate in a water stream flowing at 2 m/s
(ii) Flat plate in an airstream flowing at 2 m/s
(iii) Flat plate in an air stream flowing at 8 m/s
Result:
(i) The growth of laminar boundary layer is increased the air compared the water in same velocity
(ii) The growth of boundary layer is reduced when compared the air velocity 2 m/s to 8 m/s.
Problem - 21
A Jet plane which weights 29430 N and has area 20m2 velocity at 250 Km/ hr. When the engine delivery 7357.5 Kw. 65% of power is used to overcome the drag resistance at the wing. Calculate the co-efficient of lift and co-efficient of drag for wing. Take density of air equal to 1.21Kg/m3.
Given data:
Weight (W) = 29430N
Area (A) = 20m2
Velocity (U) = 250 Km/hr = 250 × 1000 / 3600 = 69.4m/s
Power (p) = 7357.5 Kw = 7357.5Kw = 7357.5 × 103 W
Density of air (ρ) = 1.21Kg/m3
Power used to overcome drag resistance = 65% = 0.65
To find:
(i) Co-efficient of lift (CL)
(ii) Co-efficient of Drag (CD)
Solution:
Result:
Co-efficient of lift (CL) = 0.5044
Co-efficient of drag (CD) = 1.182
Problem - 22
A thin plate measuring 75cm x 25cm is exposed parallel to a stream of water of uniform velocity 1.2 m/s. The flow takes places parallel to 25 cm side of the plate. It the kinematic viscosity of water is 11 centi stokes. Determine the maximum boundary layer thickness, shear stresses at to trailing edge and the drag on both side of the plate.
This problem is similar to Example No-35, page No-2.120
Ans:
(i) δ = 0.00239 m
(ii) τo = 0.91N/m2
(iii) FD = 1.37322N
Problem - 23
If the velocity distribution is a laminar boundary layer over a flat plate is given by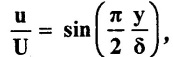 
calculate the value of δ, δ*, 0 and the shear stress.
This problem is same as Example No-24 in page No -2.62.
For determining shear stress (τo) similar to Example No: 27, page No-2.76.
Problem - 24
A horizontal pipe 50 cm in diameter and 3 Km long is discharging water at velocity of 1.5 m/s. Find the loss of head due to friction Chezy's constant is 60.
Given data:
Diameter (d) = 0.5m
Length (L) = 3Km = 3000m
Velocity (V) = 1.5m/s
Chezy's constant (C) = 60
To find:
Loss of head due to friction
Solution:
Result:
Loss of head due to friction (hf) = 15m
Problem - 25
Find the loss of head due to friction in a pipe of diameter 30 cm and length 50m, through which water is flowing at a velocity of 3m/s using arcy's formula.
Given data:
Diameter (d) = 30cm = 0.3m
Length (L) = 50m
Velocity (V) = 3m/s
To find:
Loss of head due to friction
Solution:
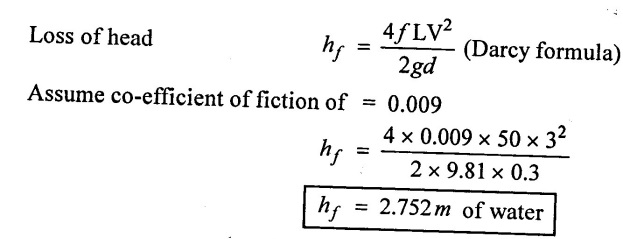
Result:
Loss of head due to friction (hf) = 2.752m of water
Problem - 26
Find the displacement thickness, the momentum thickness and energy thickness for the velocity distribution in the boundary layer is given by 
where δ = boundary lager thickness.
This problem is same as Example No - 19, page No - 2.54.
Ans:
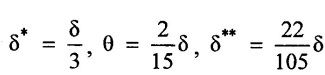
Problem - 27
The velocity distribution in the boundary is given by 
Show that the displacement thickness is 3 times the momentum thickness.
Given data:
To find:
(i) Displacement thickness (δ*)
(ii) Momentum thickness (θ)
(iii) Show the displacement thickness is 3 times the momentum thickness
Solution:
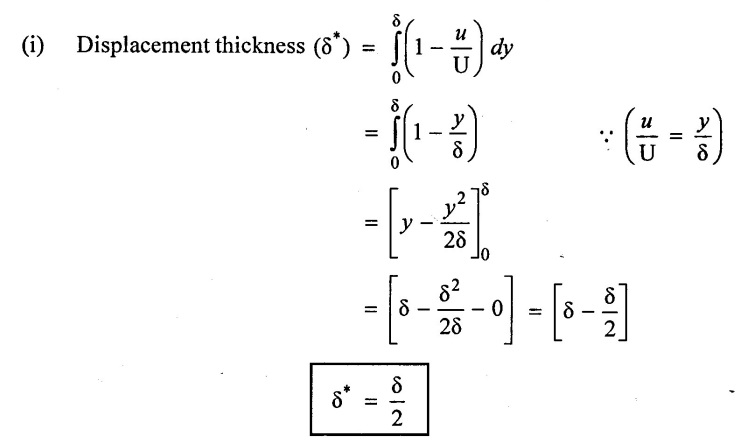
(ii) Momentum thickness
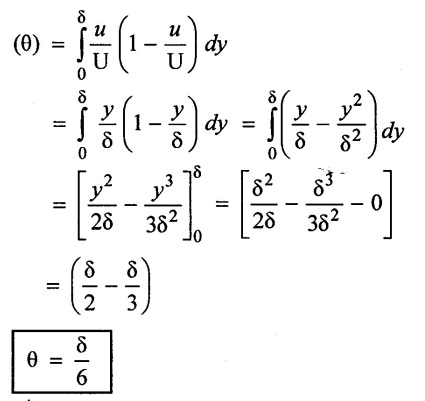
(iii) Displacement thickness δ* = 3 × momentum thickness
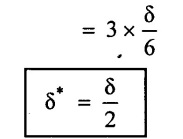
Displacement thickness is 3 times the momentum thickness
Result:
(i) Displacement thickness (δ*) = δ/2
(ii) Momentum thickness (θ) = δ/6
(iii) Displacement thickness is 3 times the momentum thickness
Problem - 28
In a pipe of diameter 350 mm, length 75 m water is flowing at a velocity of 2.8 m/s. Find the head lost due to friction using (i) Darcy-Weishbach formula (ii) chezy's formula for which C = 55. Assume kinematic viscosity of water as 0.012 stokes.
This problem is similar to Example No-45 page No - 2.127.
Ans:
(i) Using Darcy formula hƒ = 0.8473 m
(ii) Chezy's formula hƒ = 2.221m
Problem - 29
The rate of flow of water through a horizontal pipe is 0.25m3/sec. The diameter of the pipe which is 20 cm is suddenly enlarged to 40 cm. The pressure intensity in the smaller pipe is 11.772N/cm2. Determine loss of head due to sudden enlargement, pressure intensity in the larger pipe, power loss due to enlargement.
This problem is similar to Example No - 54 page No 2.139.
Ans:
he = 1.816m, p2 = 12.96 × 104 N/m2, p = 4.45Kw
Problem - 30
A horizontal pipe of diameter 500 mm is suddenly contracted to a diameter of 250 mm. The pressure intensity in the large and smaller pipe is given as 13.734 N/cm2 and 11.772 N/cm2 respectively. Find the loss of head due to contraction is Cc = 0.62. Also determine the rate of flow of water.
This problem is similar to Example No – 56 page No - 2.141.
Ans:
hc = 5.69 m2, Q = 0.2678m3/s
Problem - 31
A horizontal pipe carries water at the rate of 0.04m3/s. Its diameter which is 300 mm reduces abruptly to 150 mm. Calculate the pressure loss across the contraction. Take co-efficient of contraction = 0.62.
This problem is similar as Example No - 58, page No-2.145.
Ans:
Pressure difference (p1 − p2) = 3.35 × 103 N/m2
Problem - 32
Three pipes of diameters 300 mm, 200 mm and 400 mm and length 450 m, 255 m and 315 m respectively are connected in series. The difference in water surface levels in two tanks is 18 m. Determine the rate of flow of water if co- efficiently of frictions are 0.0075, 0.0078 and 0.0072 considering
(i) Minor losses (ii) Neglecting minor losses
This problem is similar to Example No – 69 in page No-2.177.
Ans:
(i) With minor loss (Q) = 0.0824m3/s
(ii) Without minor loss (Q) = 0.0834m3/s
Problem - 33
A main pipe divides into two parallel pipes, which again forms one pipe. The length and diameter of the first parallel pipe are 2000 m and 1 m respectively. While the length and diameter of second parallel pipe are 2000 m and 0.8 m respectively. Find the rate of flow in the main is 3m3/s. The co-efficient fo friction for each parallel pipe is same and equal to 0.005.
This problem is similar to Example No-71, Page No-2.182.
Ans:
Rate of flow in pipe (1) = 1.907 m3/sec
Rate of flow in pipe (2) = 1.0903 m3/sec
Problem - 34
Two pipes of 15 cm and 30 cm diameters are laid in parallel to pass to total discharge of 100 lits/sec. Each pipe is 250 long. Determine discharge through each pipe. Now these pipes are connected in series to connect in two tanks 500 cm apart to carry same total discharge. Determine water level difference between the tanks. Neglect minor losses in both cases and f = 0.02 for both pipes.
Given data:
Diameter at pipe – I (d1) = 15cm = 0.15m
Diameter at pipe - II (d2) = 30cm = 0.3m
Discharge (Q) = 100lits/s = 0.1m3/s
Length L1 = L2 = 250m.
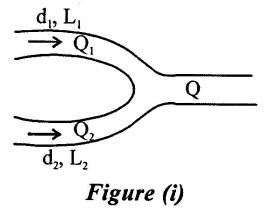
To find:
(i) Discharge in each pipe when pipes are in parallel
(ii) Difference level when pipes in series.
Solution:
Case - I pipes in parallel
(i) Area of the pipe at section (1)
(ii) Area of the pipe at section – (2)
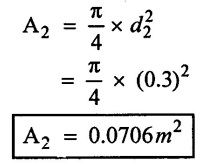
(iii) Loss of head is equal hf = hf1 = hf2
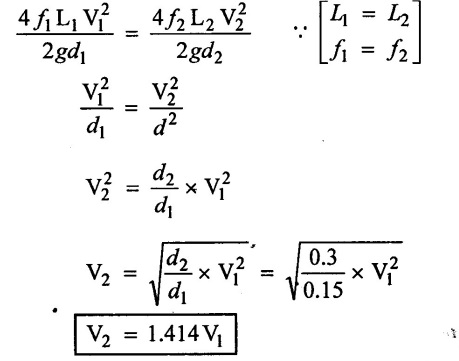
(iv) Total discharge (Q) = Q1 + Q2
(v) Discharge in pipe – I (Q1) = A1V1
= 0.0176 × 0.8512
Q1 = 0.0149m3/s
(vi) Discharge in pipe - II (Q2) = A2V2
= 0.0706 × 1.203
Q2 = 0.0849m3/s
Case (ii) pipes in series Q = Q1 = Q2
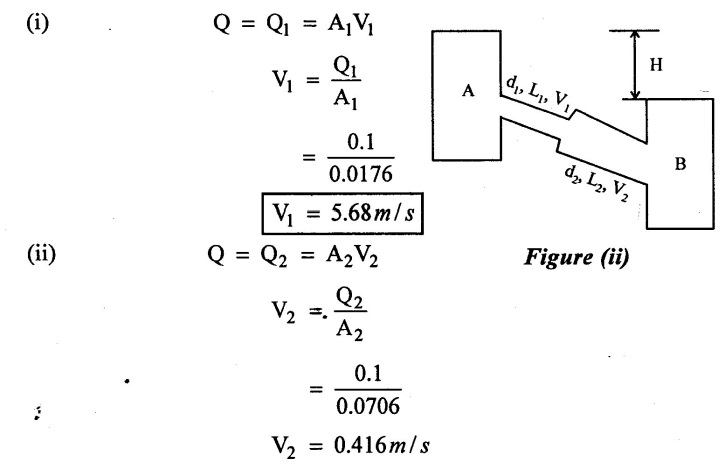
(iii) Difference level (H) = Total head loss (neglecting minor loss)
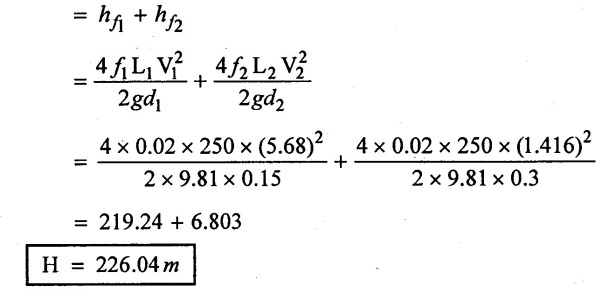
Result:
(i) Discharge in pipe − (1) (Q1) = 0.0149m3 / sec
(ii) Discharge in pipe - (2) (Q2) 0.0849 m3/sec
(iii) Difference in level (H) = 226.04 m
Problem - 35
In as city water supply system, water is flowing through a pipe line 30 cm in diameter. The pipe diameter is suddenly reduced to 20 cm. Estimate the discharge through the pipe if the difference in pressure across the sudden contraction is 5 kpa.
This problem is similar to Example No - 56 and Page No-2.141.
Ans:
Discharge (Q) = 0.0870m3/s
Problem – 36
A 100 m long pipe line of 300 mm is diameter contains two 90° elbows and two gate (wide open). Calculate the equivalent pipe length and total loss of head when the flow rate is 0.5 m3/sec, f= 0.005, and the pipe has a sharp entry and exit.
Given data:
Pipe length (L) = 100 m
Discharge (Q) = 0.5m3 / s
No. of Elbows (90°) = 2
Diameter (D) = 300mm = 0.3m
Friction co-efficient (f) = 0.005
No. of Gate valve = 2
Assume
For elbow short radius = 0.9 = kE
Gate value wide (or) fully open = 0.2 = ka
To find:
(i) Equivalent length
(ii) Total loss of head
Solution:
(iv) Loss of head due to Elbow
(v) Loss of head due to Gate valve (wide open)
(vi) Total loss of head (h) in pipe line
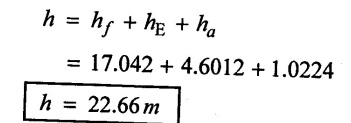
(vii) Total head loss in equivalent pipe = Total loss of head in pipe line
Result:
(i) Total head loss (h) = 22.66 m
(ii) Equivalent length (Le) = 133.04m
Problem - 37
For town water supply, a main pipe line of diameter 0.4 m is required. As pipes more than 0.35 m diameter are not readily available, two parallel pipes of same diameter are used for water supply. If the total discharge in the parallel pipes are same as in single main pipe. Find the diameter of parallel pipe. Assume co-efficient of discharge to be same for all pipes.
Given data:
Required pipe diameter (d) = 0.4m
To find:
Diameter of parallel pipe
Solution:
(i) For a single pipe system (d) = 0.4m
(ii) For a parallel pipes (Q) = Q1 + Q2
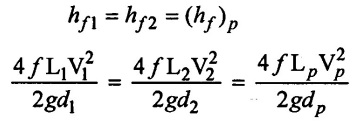
It is given that the total discharge in the parallel pipes are same as in single main pipe, So the both head losses are equal.
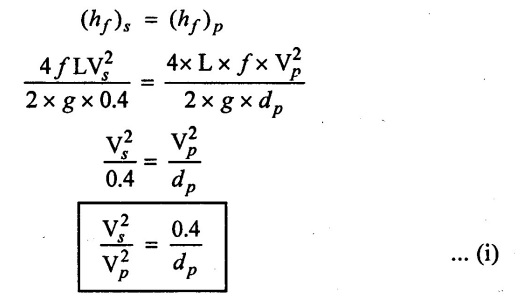
(iii) Using continuity equation
Result:
Diameter of parallel pipe (dp) = 0.303m
Problem - 38
A 150 mm diameter pipe reduces in diameter abruptly to 100 mm diameter. If the pipe carries water at 30 lit per sec. Calculate pressure loss across the contraction. Take the co-efficient of contraction of contraction as 0.6.
This problem is similar to Example No - 58 and Page No-2.145.
Ans:
Pressure loss (p1 - p2) = 9.09 × 103 N/m2
Problem - 39
A pipe line 20 cm in diameter 70 m long conveys oil of specific gravity 0.95 and viscosity 0.23 N-s/m2. If the velocity of oil is 1.38 m/s. Find the difference in pressure between the two ends of the pipe.
Given data:
Diameter (d) = 20 cm = 0.2m
Specific gravity (S) = 0.95
Velocity (V) = 1.38m/s
Length (L) = 70m
Viscosity (μ) = 0.23N - s/m2
To find:
Pressure difference (p1 - p2)
Solution:
Result:
Pressure difference (p1 - p2) = 17774.4 N / m2
Problem - 40
A horizontal pipe has an abrupt expansion from 10 cm to 16 cm. The water velocity in the smaller section is 12 m/s and the flow is turbulent. The pressure in the smaller section is 300 kpa. Determine the downstream pressure and estimate the error that would have occurred Bernoulli's equation had used.
Given data:
Diameter at upstream side (d1) = 10cm = 0.1m
Diameter at downstream side (d2) = 16cm = 0.16m
Velocity at upstream side (V1) = 10m/s
Pressure at upstream side (p1) = 300 kpa = 300 × 103 N/m2
To find:
(i) Pressure at downstream side (p2)
(ii) % of error when Bernoulli's equations used without minor losses
Solution:
(vii) Apply Bernoulli's equation without losses
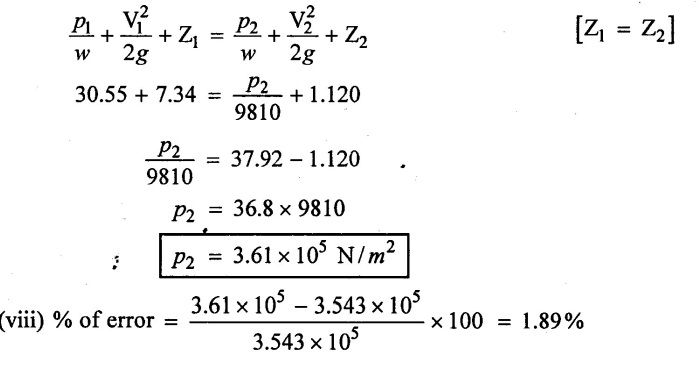
Result:
(i) Downstream pressure (p2) = 3.342 × 105 N/m2 (ii) % of error = 1.89%
Problem - 41
Two pipes of diameter 40 cm and 20 cm are each 300 am long. When pipes are connected in series and 0.10m3/s. The same total discharge when pipes connected in parallel. Take ƒ = 0.0075 for each pipe. Find the loss of head for both cases.
Given data:
Diameter at (1) (d1) = 40cm = 0.4m
Diameter at (2) (d2) = 20cm = 0.2m
Length (L1) = (L2) = 300m
Discharge (Q) = 0.10m3/s
Co-efficient of friction (f) = 0.0075
To find:
Loss of head
(i) Pipes in series (ii) Pipes in parallel
Solution:
Result:
Loss of head when
(i) Pipes in series (h) = 23.9m
(ii) Pipe in parallel (hf1) = 0.71m
Problem - 42
Determine the equivalent pipe corresponding to 3 pipes in series with lengths and diameters I1,I2,I3 and d1,d2,d3 respectively.
This equation is same as in page No-2.169 to 2.171.
Problem - 43
A pipe increases in diameter suddenly from 12 cm to 22 cm if the discharge of water through the pipe is 120 lit/sec. Determine the loss of head due to sudden enlargement and also determine the difference of pressure between two sections.
This problem is similar to Example No – 54 and Page No - 2.139.
Ans:
(i) Loss of head due to sudden enlargement he = 2.838m
(ii) Pressure difference (p2 - p1) = 23544N/m2
Problem - 44
An existing 300 mm diameter pipe line of 3200 m length connects two reservoirs having 13 m difference in their water levels. Calculate the discharge (Q1). If a parallel pipe 300 mm is diameter is attached to the last 1600 m length of the above existing pipe line find the new discharge (Q2). What is the change in discharge? Express it as percentage of Q1. Assume friction factor f = 0.04 in Darcy weishbach formula.
This problem is similar to Example No - 83 and Page No - 2.202.
(i) Discharge (Q1) = 0.05466m3/sec
(ii) Discharge (Q2) = 0.0691m3/sec
(iii) Increase in discharge (Q) = 26.42%
Problem - 45
A pipe 10 km, long delivers a power of 50 Kw at its outlet end. The pressure at inlet is 5000KN/m2 and pressure drop per Km of pipe line is 50 KN/m2. Find the size of the pipe and efficiency of transmission. Take 4f = 0.02.
This problem is similar to Example No - 78 and Page No -2.193.
Ans:
(i) Diameter of pipe (D) = 0.131m
(ii) Efficiency of power transmission (η) = 90%
Problem - 46
A 2500 m long pipe line is used for transmission of power 120 Kw is to be transmitted through the pipe in which water having a pressure of 4000 KN/m2 at inlet is flowing. If the pressure drop over the length of pope is 8000 KN/m2 and ƒ = 0.006 find
(i) Diameter of pipe
(ii) Efficiency of transmission
This problem is similar to Example No - 78 and Page No -2.193.
Ans:
(i) Diameter of pipe (D) = 0.1535m
(ii) Efficiency of power transmission (η) = 80%
Problem - 47
A power transmission pipe of 10 cm diameter and 500 m long is fitted with a nozzle at exit, the inlet is from a river, with water level 60 m above the discharge nozzle. Assume ƒ = 0.02. Calculate the maximum power which can be transmitted and diameter of nozzle required.
Given data:
Length (L) = 500m
Diameter (D) = 10cm = 0.1m
Head of pipe at inlet (H) = 60m
Co-efficient of friction (ƒ) = 0.02
To find:
(i) Maximum power
(ii) Diameter of nozzle (d)
Solution:
(i) Diameter of nozzle (d) in maximum power transmitted
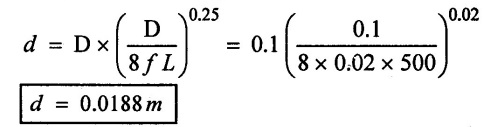
(ii) Maximum power transmission conditions
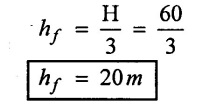
(iii) Loss of head
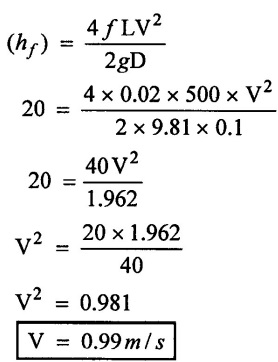
(iv) Discharge (Q) = A × V
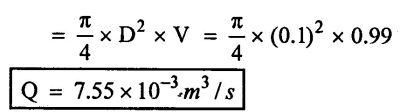
(v) Maximum power (p) = w × Q × H*
= 9810 × 7.775 × 10-3 × (60 - 20)
= 3.05 × 103 watts
p = 3.05 Kw
Result:
(i) Diameter of nozzle (d) = 0.0188m
(ii) Maximum power transmission = (p) = 0.05 Kw
Problem - 48
Determine the length of an equivalent pipe of diameter 20 cm and friction factor 0.02 for a given pipe system, discharging 0.1m3/s. The pipe system consists of the following
(i) A 10 m line of 20 cm diameter with f = 0.03
(ii) Three 90° bend k = 0.5 for each
(iii) Two sudden expansion of diameter 20 to 30 cm
(iv) A 15 cm line of 30 cm diameter with f = 0.025 and
(v) A global valve fully open (k = 10)
This problem is similar to Example No - 79, page No-2.195.
Ans:
Equivalent length Le = 47.75m
Problem - 49
A compound piping system consists of 1800 m of 0.5 m, 1200 m of 0.4 m and 600 m of 0.3 m new cast-iron pipes connected series cover the system to
(i) An equivalent length of 0.4 m diameter
(ii) An equivalent size of pipe of 3600 m length.
This problem is similar to Example No – 76 page No-2.191.
Ans:
L = 4318.22 m, D = 0.386 m
Problem - 50
The main pipe is divided into two parallel pipes which again forms one pipe, the first parallel pipe has length of 1000 m and diameter of 0.8 m. The second parallel pipes has length of 1000 m and diameter 0.6 m. The co-efficient of friction for each parallel pipe is 0.005. If the total rate of flow in the main pipe is 2m3/sec find the rate of flow in each parallel pipe.
Given data:
L1 =1000m,
d1 = 0.8m,
d2 = 0.6m,
f1 = ƒ2 = 0.005,
L2 = 1000m,
Q = 2m3/s
To find:
Discharge of each pipe in parallel
Solution:
(i) Loss of head is equal in parallel pipes
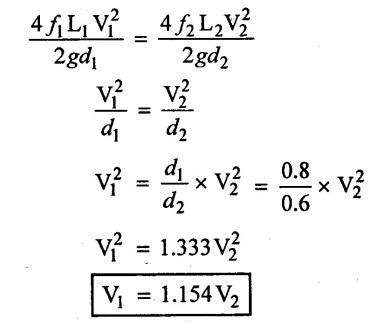
(ii) Rate of flow in pipe (1)
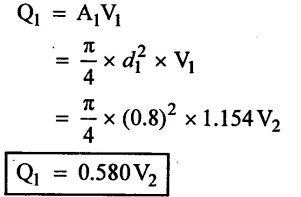
(iii) Rate of flow in pipe (2)
Q2 = A2 × V2
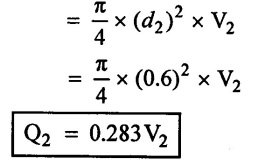
(iv) Total rate of flow (Q) = Q1 + Q2
2 = 0.58 V2 + 0.283 V2
2 = 0.863 V2
Result:
(i) Discharge at pipe (1) (Q1) = 1.345m3/s
(ii) Discharge at pipe (2) (Q2) = 0.655m3/s
No comments:
Post a Comment