Problem - 1
A pelton wheel has to be designed for the following data, HP to be developed = 8500
Net head available = 280 m
RPM = 650
Ratio of jet diameter to wheel diameter = 1/9
Mechanical efficiency = 88%
Find the number of jets, diameter of jet, diameter of wheel and quantity of water required.
This problem is similar to Example No -5 in Page No: 5.66
Assume Cv = 0.985 Ku = 0.45
Ans: Diameter of wheel (D) = 0.979m. (1HP = 746 w)
Diameter of jet (d) = 0.109m
Number of jet = 4
Quantity of water required (Q) = 2.586m3/s
Problem - 2
A Francis turbine working under a head of 20m is supplied with 1.5 m3/sec of water. Wheel diameter at the entrance and exit are 1m and 0.6 m respectively. It is developing 300HP at 300 rpm. Velocity of water at exit is 3m/s. Assuming wheel width is constant. Find (i) Theoritical hydraulic efficiency. (ii) Actual efficiency (iii) Suitable anges of guide vanes and runner vanes at inlet.
Given data:
Head (H) = 20m
Discharge (Q) = 1.5 m3/s
Wheel diameter at inlet (D1) = 1m
Wheel diameter at outlet (D2) = 0.6 m
Power (P) = 300 HP
Speed (N) = 300 rpm
Velocity of flow at outlet (Vf2) = 3m/s
To find:
(i) Hydraulic efficiency (ηh)
(ii) Guide vane angles at inlet (α)
(iii) Vane angle at inlet (θ)
Solution:

(v) From inlet triangles

(vi) Hydraulic efficiency
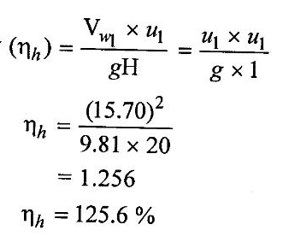
This is actual Hydraulic efficiency but Practically not possible, so Select minimum head of francis turbine H = 60m.
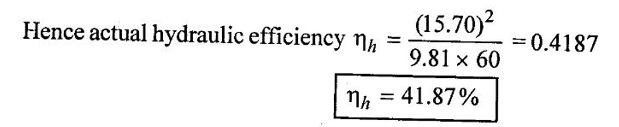
Result:
(i) Actual efficiency (ηh) = 41.87%
(ii) Inlet guide angle (α) = 6.54°
(iii) Inlet vane angle (θ) = 60.90°
Problem - 3
A kaplan turbine delivery 40 MW works under a head of 40m and runs at 150 rpm. The hub diameter is 3m and runner tip diameter is 6m. The overall efficiency is 90%. Determine the blade angles at the hub and of the runner tip, and also at a diameter of 6 m also find the speed ratio and flow ratio based on tip velocity. Assume hydraulic efficiency as 95%.
Given data:
Power (P) = 40 MW = 40 × 106w
Head (P) = 40m
Speed(N) = 150 rpm
Diameter of hub (Db) = 3m
Outer diameter of runner (Do) = 6m
Over efficiency (ηo) = 90% = 0.90
Hydraulic efficiency (ηh) = 95% = 0.95
To find:
(i) Blade angles at the hub
(ii) Blade angles at the tip of runner
(iii) Speed ratio and flow ratio based on tip velocity.
Solution:

(3) Blade angles of extreme edge (or) tip of the runner.

Result:
(i) Vane angles at the hub (θ) = 115.78°
ϕ = 34.21°.
(ii) Vane angles at the tip (θ) = 157.80°
ϕ = 18.77°
(iii) Speed ratio (ku) = 1.68
(iv) Flow ratio (kƒ) = 0.57
Problem - 4
A Pelton wheel is receiving water from a Destocked with a gross head of 500m. One-third of gross head is lost in friction in the penstock. The rate of flow through the nozzle from the end of the penstock i 2.2 m3/s. The angle of deflection of the jet is 165°, Determine
(i) The power given by water to the runner and
(ii) Hydraulic efficiency of the Pelton wheel
Take Cv = 1.0 & speed ratio = 0.1,
This problem is similar to Example No-1 and Page No : 5.56.
Answer:
Power (P) = 7.0261 × 103 kw
Hydraulic efficiency (ηh) = 97.66%
Problem - 5
The following data is related to Pelton wheel shaft power = 9600 kw
Head = 370 m
Speed = 750 rpm, Overall efficiency = 85%
Jet diameter is not to exceed 1/6th of the wheel diameter.
Determine the following
(i) Wheel diameter
(ii) Diameter of jet
(iii) Number of jets required
Take Cv = 0.985, Speed ratio = 0.45
This problem is similar to Example No-5 and Page No : 5.66
Ans:
Diameter of wheel (D) = 0.9763m
Diameter of jet (d) = 0.1627 m
No. of jets = 2
Problem - 6
Determine the rpm, work done per second, power and overall efficiency of a Pelton wheel from the following data. Head = 150m, wheel diameter = 0.75m. Jet diameter = 4cm, deflection angle of buckets = 172o, Cv of nozzle = 0.48, speed ratio = 0.42 and surface roughness factor of vanes 0.97
Given data:
H = 150m
D = 4 cm = 0.04m
Cv = 0.98
k = 0.97
D = 0.75 m
ϕ = 180-172 = 800
ku = 0.42
Vr2 = 0.97 Vr1
To find:
(i) Speed (w)
(ii) Work done /sec
(iii) Power
(iv) Overall efficiency
Solution:
(i) Velocity of jet at inlet is
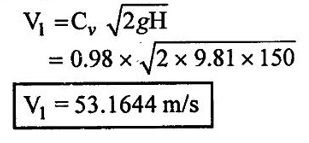
(ii) Velocity of wheel is
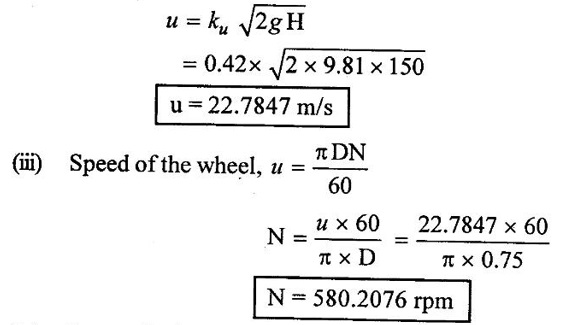
(iv) From velocity triangles

(vi) Overall efficiency:
Assume mechanical efficiency ηm = 0.9
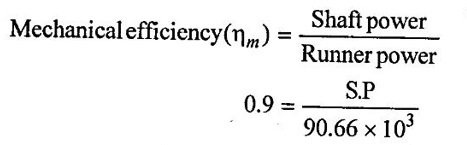
Shaft power = 81.59 × 103 watts
Overall efficiency,

Result:
(i) Speed (N) = 580.2076 rpm
(ii) Work done/sec = 90.66 × 103 N-m/s
(iv) Overall efficiency = 83%
(iii) Power = 90.66 × 103 watts
Problem - 7
A pelton wheel has a mean bucket speed of 10m/s with a jet of water flowing at the rate of 0.7m3/s. Under a head of 30m. If the buckets deflect the jet through an angle of 160°. Calculate the power given by water to the runner and hydraulic efficiency of turbine. Assume the coefficient of velocity of 0.98:
This problem is similar to Example No:3 and Page No:5.61
Ans:
(i) Power (P) = 187.046 kw
(ii) Hydraulic efficiency (ηh) = 94.53%
Problem - 8
Determine the HP of the Pelton wheel with tangential velocity 20m/s, head 50 m, discharge 0.03 m3/s, side clearance angle 15o. Take Cv as 0.975.
Given data:
Bucket velocity, u = 20m/s
Head, H = 50m,
Discharge, Q = 0.03 m3/s
Outlet vane angle, ϕ = 15°
Coefficient of velocity, Cv = 0.975
To find:
Horse power (HP)
Solution:
(i) Velocity of jet is,
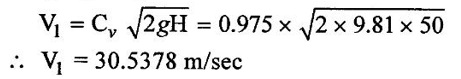
(ii) Workdone per second is also given by,
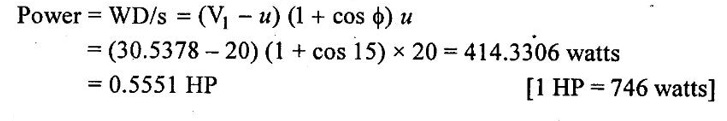
Result:
Power P = 0.5551 HP
Problem - 9
The mean velocity of the buckets of the pelton wheel is 10m/s. The jet supplies water at 0.7 m3/s at head of 30m. The jet is deflected through an angle 160° by the bucket. Find the hydraulic efficiency. Take Cv = 0.98.
This problem is similar to Example No:3 and Page No:5.61
Ans:
Hydraulic efficiency (ηh) = 94.53%
Problem - 10
A Pelton turbine is to produce 18mw under a head of 450m, when running at 480 rpm. If D/d ratio is 10, determine the number of jets required. Assume overall efficiency 100%
This problem is similar to Example no: 5 and Page No: 5.66
(Assume Cv = 0.97, ku = 0.46)
Ans:
Number of jets = 2 Nos
Problem - 11
A pelton wheel works under a net head of 600m and it runs at a speed of 700 rpm. The mean diameter of runner is 1.35 m. For discharge rate of 0.22 m3/ sec. Find the power available at the nozzle and hydraulic efficiency of turbine. Assume no frictional losses in nozzle and over the buckets and outlet clearance angle is 15o. Assume Cv = 0.98
This problem is similar to Example No:3 and Page No : 5.61
Ans:
(i) Power (P) = 1.294 × 103 kw
(ii) Hydraulic efficiency (ηh) = 97.825%
Problem - 12
The nozzle of a pelton wheel gives a jet of 9cm diameter and velocity 75m/s. Coefficient of velocity is 0.978. The pitch circle diameter is 1.5m and the deflection angle of the bucket is 170o. The wheel velocity is 0.46 times the jet velocity. Estimate the speed of the pelton wheel turbine in rpm, theoretical power developed and also the efficiency of the turbine.
Given data:
Diameter of jet, d = 9cm = 0.09m
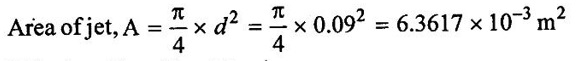
Velocity of jet, V1 = 75 m/s
Coefficient of velocity, Cv = 0.978
Pitch circle diameter, D= 1.5 m
Angle of deflection = 170°
ϕ = 180 – 170 = 10o.
Velocity of wheel, u = 0.46 V1
To find:
(i) Speed of the pelton wheel turbine N
(ii) Theoretical powe, P
(iii) Efficiency of turbine, η
Solution:
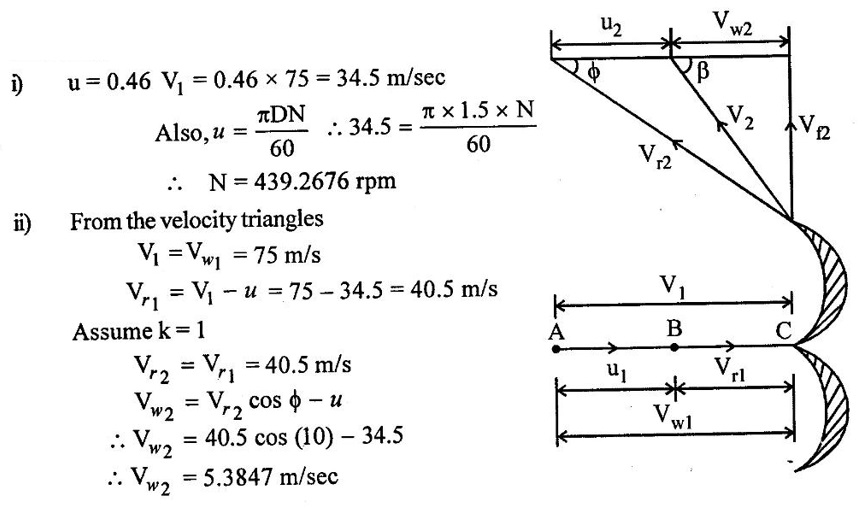
(iii) Now the work done per second (or) Runner power

Results:
(i) Speed of pelton wheel, N = 439.2676 rpm
(ii) Theoretical power developed, P = 1.3232 × 103 kw
(iii) Efficiency of turbine, ηo = 94.31%
Problem - 13
A dam on a river is being suited for a hydraulic turbine. The flow rate is 1600 m3/h, the available head is 25m and the speed of turbine is 460 rpm. Discuss the estimate turbine size and feasibility for a Francis turbine and a pelton wheel.
Given data:
Flow rate, Q = 1600 m3/h = 1600 / 60 × 60 = 0.4444 m3/s
Head, H = 25m
Speed of turbine, N = 460 rpm
Assume overall efficiency = 90%
To find:
Size and type of turbine
Solution:
(i) The overall efficiency of the turbine is
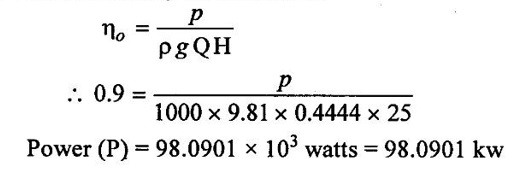
(ii) The specific speed of turbine is,
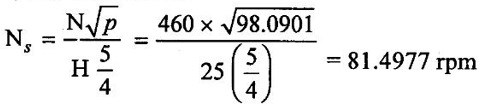
Result:
As the specific speed varies between 51 to 225 rpm, thefrancis turbine is feasilde.
Problem - 14
In a hydroelectric station, water is available at the rate of 175 m3/s under head of 18m. The turbine runs at speed of 150 rpm, with overall efficiency 82%. Find the number of turbines required if they have the maximum specific speed of 460 rpm.
Given data:
Rate of water, Q = 175 m3/s
Head, H = 18 m
Speed of turbine, N = 150 rpm
Overall efficiency, ηo = 82% = 0.82
Maximum specific speed, Ns = 460 rpm
To find:
Number pf turbones
Solution:
(i) Specific speed of turbine is,
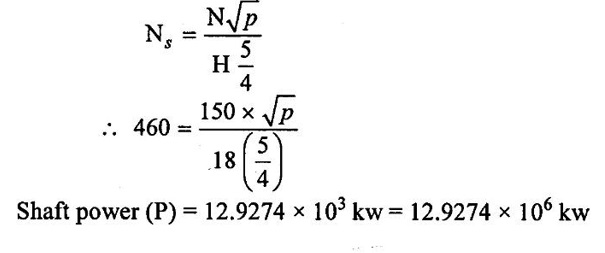
(ii) Power available at the inlet of turbine
Ptotal = ρg QH × ηo = 1000 × 9.81 × 175 × 18 × 0.82
⸫ Ptotal = 25.3392 × 106 w
(iii) No of turbines n = 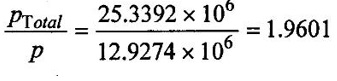
Result:
No of turbines, n = 2
Problem - 15
A turbine is to operate under a head of 25 m at 200 rpm. The available discharge is 9 m3/s. Assuming an efficiency of 90%. Determine (i) Specific speed (ii) Power generated (iii) Performance under a head of 20m and (iv) Type of the turbine.
Given data:
Head, H = 25m,
Speed of turbine, N = 200 rpm,
Discharge, Q = 9m3/s
Efficiency, ηo = 90% = 0.9
To find:
(i) Specific speed, Ns
(ii) Power generated, p
(iii) Performance under H = 20m
(iv) Type of turbine
Solution:
(i) The overall efficiency of turbine is,
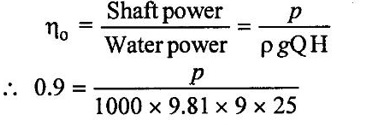
= 1.9865 × 106w = 1.9865 × 103 kw
(ii) The specific speed of turbine is
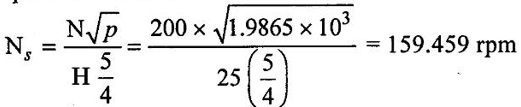
(iii) Speed of turbine under head of 20m,
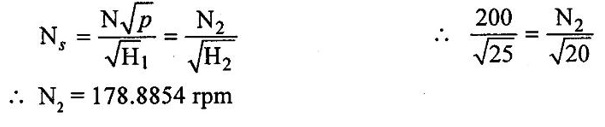
(iv) Discharge of turbine under head of 20m,

⸫ Q2 = 8.0498 m3/sec
(v) Power developed by turbine under head of 20m,
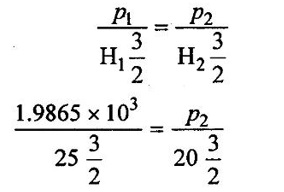
p2 = 1.4214 × 103 kw
Result:
(i) Specific speed, Ns = 159.459 rpm
(ii) Power generted, p = 1.9865 × ́103 kw
(iii) Performance under a head of 20m is, p2 = 1.4214 × 103 kw
(iv) Type of the turbine: As the specific speed lies between 150 to 250 rpm the turbine selected is medium head francis turbine.
Problem - 16
The hub diameter of a Kaplan turbine working under a head of 12m, is 0.35 times the diameter of the runner. The turbine is running at 100 rpm. If the vane angle of the extreme edge of the runner of outlet is 15o and flow ratio is 0.6. Find the diameter of the bass and the discharge through the runner. The velocity of the whirl is given as zero
This problem is same as Example No: 43 and Page No: 5.171
Problem - 17
A Kaplan turbine delivers 10 MW under a head of 25m. The hub and tip diameters are 1.2m and 3m. Hydraulic and overall efficiencies are 0.90 and 0.85. If both velocity triangles are right angled triangles, determine the speed, guide blade inlet angle and blade outlet angle.
Given data:
Shaft power = SP = 10 MW = 10 × 106 w
Head, H = 25 m
Diameter of hub, Dh = 1.2 m,
Diameter of tip, Do = 3m,
Overall efficiency, ηo = 0.85
Hydraulic efficiency, ηh = 0.9
θ = 90°; since velocity triangles are right angle
⸫ Vƒ1 = Vr1 & u1 = Vw1
β = 90°
⸫ Vƒ2 = V2 &Vw2 = 0
To find:
(i) Speed of the turbine
(ii) Guide blade inlet & outlet angle
Solution:
(i) The overall efficiency for turbine is,
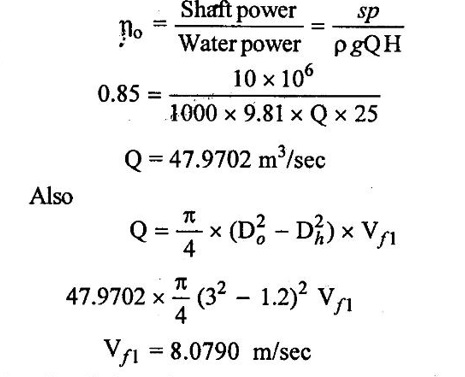
(ii) Hydraulic efficiency is,
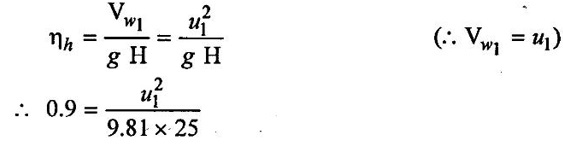
u1 = 14.8568 m/sec
Also,
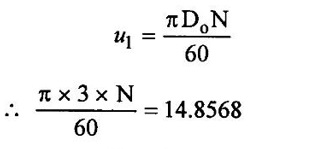
N = 94.5814 rpm
(iii) From inlet velocity triangle,
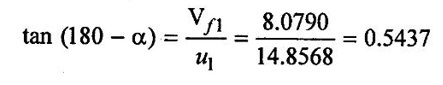
180 - α= 28.5369°
⸫ α = 151.4630°
(iv) For kaplan turbine, u2 = u1 = 14.8568 m/sec
Vƒ2 = Vƒ1 = 8.0790 m / sec
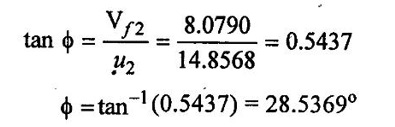
Problem - 18
A Kaplan turbine working under a head of 25 cm develops 12 MW shaft power. The outer diameter of the runner is 3m and hub diameter is 1.5m. The guide blade angle at the extreme edge of the runner is 32o. The hydraulic and overall efficiencies of the turbine are 87% and 84% respectively. If the velocity of whirl is zero at outlet, determine:
(i) Runner vane angles at inlet and outlet at the extreme edge of the runner and
(ii) Speed of the turbine.
This problem is similar to Example No: 41 and Page No: 5.165.
Ans:
(i) Runner vane angles θ = 63.6210°
ϕ = 42.1603°
(ii) Speed, N = 77.2499 rpm
Problem - 19
A Kaplan turbine runner is to be developed 9000 kw. The net available head is 5.5m. If the speed ratio = 2, flow ratio = 0.7, overall efficiency = 87% and the diameter of the boss is 1/3 the diameter of the runner. Find the diameter of the runner and boss, its speed and specific speed of the turbine.
This problem is similar to Example No: 42 and Page No: 5.169
Ans:
(i) Diameter of runner (Do) = 6.1456 m
(ii) Diameter of boss (Db) = 2.0485 m
(iii) Speed, N = 67.7932 rpm
(iv) Specific speed (Ns) = 763.579 rpm
Problem - 20
A Francis turbine with an overall efficiency of 80% is required to produce 130kw. It is working under a head of 10m. The peripheral velocity is 0.24 √√2 g H and the radial velocity of flow at inlet is 0.9 √2 g H. The wheel runs at 150 rpm and the hydraulic løsses in the turbines are 10% of the available energy. Assuming radial discharge. Determine:
(i) The guide blade angle
(ii) The wheel vane angle at inlet,
(iii) Diameter of the wheel at inlet
(iv) Width of the wheel at inlet
This problem is similar to Example No:33 and Page No:5.140
Ans:
(i) Guide angle (α) = 25.64°
(ii) Vane angle (θ) = 28.83°
(iii) Diameter (D1) = 0.4280 m
(iv) Width (B1) = 0.0977 m
Problem - 21
A Francis turbine developing 16120 kw under a head of 260m runs at 600 rpm. The runner outside diameter is 1500 mm and the width is 135mm. The flow rate is 7 m3/s. The exit velocity at the draft tube outlet is 16m/s. Assuming zero whirl velocity at exit and neglecting blade thickness determine the overall and hydraulic efficiency and rotor blade angle at inlet. Also find the guide vane outlet angle.
This problem is same as Example No: 35 and Page No: 5.148
Problem - 22
The following data is given for a Francis turbine. Net head H = 60m, speed N = 700 rpm shaft power = 294.3 kw, overall efficiency = 84%, hydraulic efficiency = 93%, flow ratio = 0.20, breadth ratio n = 0.1, outer diameter of runner = 2 × inner diameter of runner, the thickness of vanes occupies 5% of circum ferential area of runner, velocity of flow is constant at inlet and outlet and discharge is radial at outlet.
Determine:
(i) Guide blade angle
(ii) Runner vane angle at inlet and outlet
(iii) Diameter of runner at inlet and outlet
(iv) Width of the wheel at inlet
This problem is similar to Example No:34
Ans:
Guide blade angle (α) = 13.92°
(ii) Inlet vane angle (θ) = 40.81°
(iii) Outlet vane angle (ϕ) = 34.78°
(iv) Diameter of runner inlet (D1) = 0.5391 m
(v) Diameter of runner outlet (D2) = 0.2695m
(vi) Width at inlet (B1) = 0.05391 m
Problem - 23
In an inward radial flow turbine, water enters at an angle of 22o to the wheel tangent to the outer rim and leaves at 3m/sec. The inner and outlet diameters are 300mm and 600mm respectively. The speed of the runner is 300 rpm. The discharge speed of the runner is 300 rpm. The discharge through the runner is radial.
Find:
(i) Inlet and outlet blade angles
(ii) Taking inlet width as 150 mm and neglecting the thickness of the blades, find the power developed by the turbine.
This problem is same as Example No: 26
Problem - 24
An outward flow reaction turbine has internal and external diameters of the runner as 0.5 m and 1m respectively. The turbine is running at 250 rpm and rate of flow of water through the turbine is 8 m3/sec. The width of the runner is constant at inlet and outlet is 30cm. The head on the turbine is 10m and discharge at outlet is radial. Determine
(i) Vane angle at inlet and outlet
(ii) Velocity of flow at inlet and outlet
This problem is similar to Example No:32 and Page No: 5.138
Ans:
(i) Vane angle at inlet, θ = 80.17°
(ii) Vane angle at outlet, ϕ = 32.96°
(iii) Velocity of flow at inlet, Vf1 = 16.97 m/s
(iv) Velocity of flow at outlet, Vƒ2 = 8.48 m/s
Problem - 25
a) Show that the hydraulic efficiency for a Francis turbine having velocity of flow through runner as constant, is given by the relation,
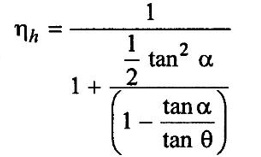
Where α = Guide blade angle and θ = Runner vane angle at inlet
The turbine is having discharge at outlet
b) If vanes are radial at inlet, than show 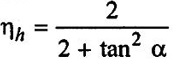
Given data:
Vf1 = Vf2; If discharge is radial Vw2 =0, Vƒ2 = V2
Case (i):
From inlet velocity triangle,
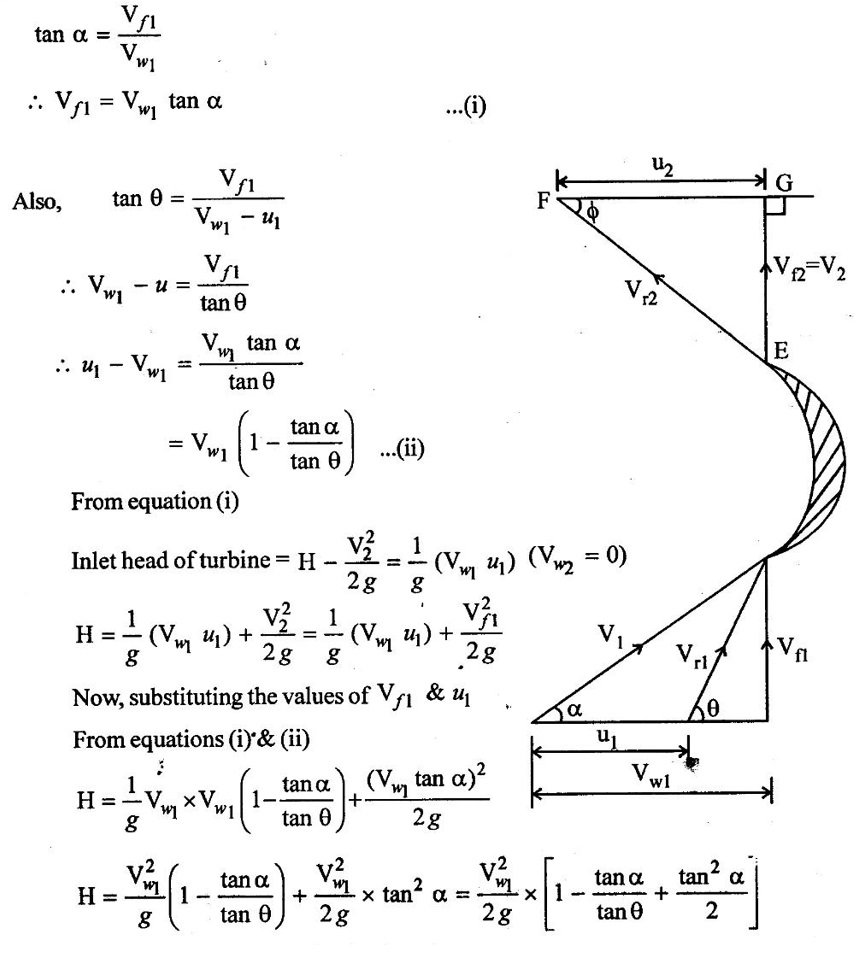
The hydraulic efficiency of turbine is given by
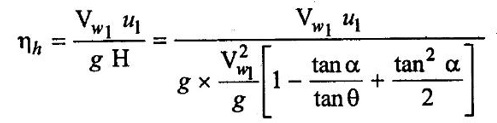
Substituting the vale of u1 from equation (ii)
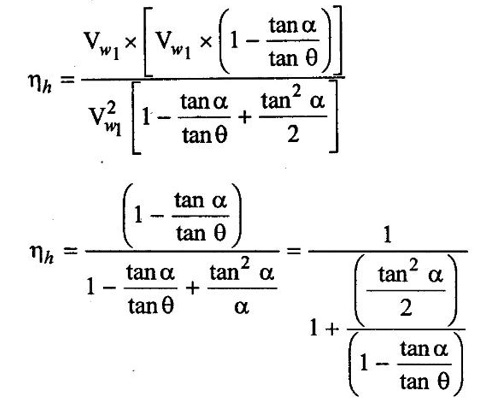
Case (ii):
If vane angle θ = 90°; then the flow is radial at inlet
Substitute θ = 90° in equation (iii) We get,
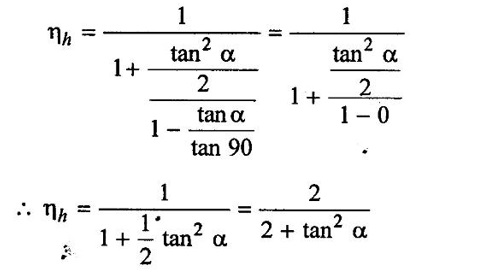
Problem - 26
A reaction turbine works at 400 r.p.m under a head of 90 meters. Its diameter at inlet is 120 cm and the flow area is 0.35 m2. The angles made by absolute and relatives velocity at inlet are 10° & 60° respectively with the tangential velocity. Determine.
(i) The volume flow rate
(ii) The power developed
(iii) Hydraulic efficiency.
This problem is similar to Example No:28
Ans:
(i) Volume flow rate (Q) = 1.7265 m3/s
(i) Power (p) = 1214.1318 kw
(iii) Hydraulic efficiency ηh = 79.65%
No comments:
Post a Comment