1. Pipes in Series (or) Compound Pipe
In piping systems, when the pipes of different lengths and diameter are connected end to end is called pipes in series (or) compound pipes. Let as the pipes in series as shown in figure 2.30.
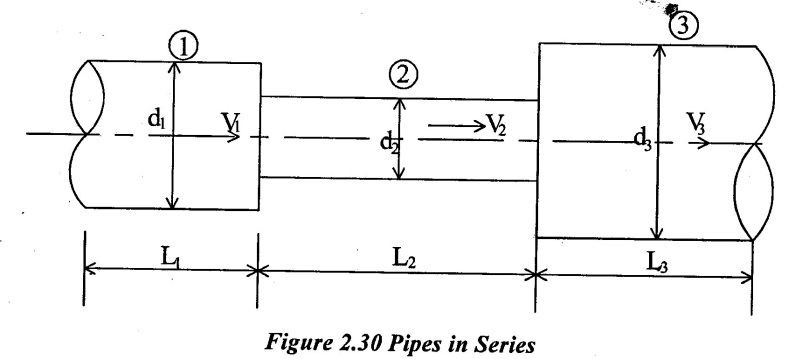
Where,
L1 L2, L3 - Length of pipes 1,2, & 3 respectively
d1, d2, d3 - diameter of pipes 1, 2, & 3 respectively
V1 V2 & V3 - Velocity of flow through pipes 1,2,& 3 respectively.
f1 f2 & f3 - Co-efficient of friction for pipes 1,2 & 3 respectively
The rate of flow through the entire system remains constant, regardless of the diameter of the individual pipes in the system. This is natural consequence of the conservation mass principle for steady incompressible flow.
Hence
Rate of flow at pipe (1) (Q1) = Rate of flow at pipe (2) (Q2) = Rate of flow at pipe (3)(Q3)
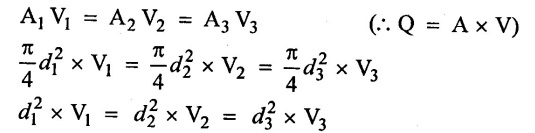
The total head loss in this case is equal to the sum of the head losses in individual pipes in the system, including the minor losses.

2. Two Reservoirs are Connected Through Pipes in Series.

The pipe line connecting two reservoirs by pipes. Then the difference in liquid surface level is equal to the sum of the head losses in all the sections as shown in figure 2.31.
Let Q = Discharge through the pipe line
H = Total loss of head
d1 = Diameter of pipe - I
L1 = Length of pipe - I
f1 = Co-efficient friction in pipe - I
d2, L2, f2 = corresponding value of pipe -2
d3, L3, f3 = corrsponding value of pipe -3
Case (i) consider the losses
Total loss of head (H) = Major losses + minor losses
Major losses = Head loss due to friction in each pipes.
= hƒ1 + hƒ2 + hƒ3
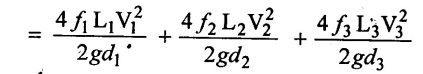
Minor losses = Entrance loss + contraction loss + Expansion loss + Exit loss
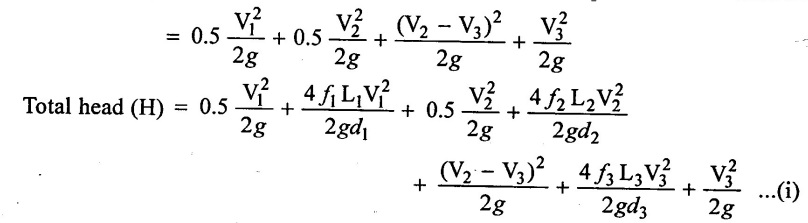
Case(ii) Neglect the minor loss.
Total head loss (H) = Major losses
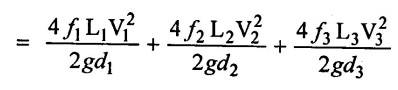
Applying Bernoulli's equation at points A & B on the free surface of liquid in reservoirs.
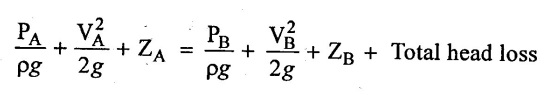
0 + 0 + ZA = 0 + 0 + ZB + total head loss
ZA - ZB = total head loss …(ii)
H = Total head loss.
Case (iii) If the discharge through pipe is given, Then
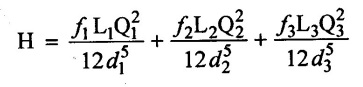
3. Pipes in Parallel.
If a pipe line divides into two (or) more pipes for some distance and these pipes again join together at some distance at down stream side as shown in figure 2.32. Then these pipes are said to be parallel. In order to increase the discharge, pipes are connected in parallel.
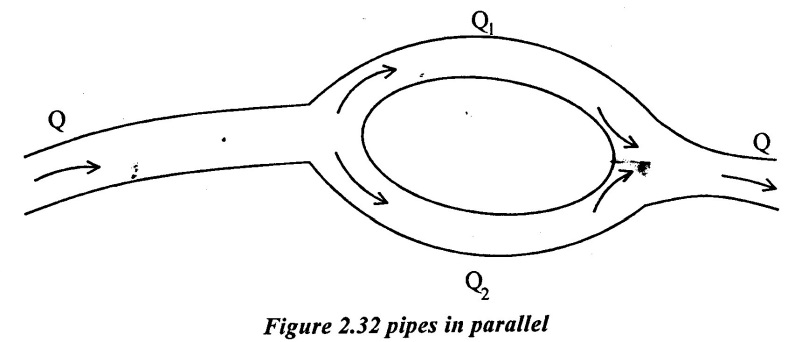
The parallel pipes follow the following conditions
(i) Discharge in main is equal to sum of discharges in each parallel pipes
Q = Q1 + Q2 ...(i)
(ii) Loss of head in each parallel pipe is same

4. Equivalent pipe
A compound pipe (or) series pipe which is consist of several pipes of different length and diameters to be replaced by a pipe of uniform diameter and the same length as that of the compound pipe, is called as equivalent pipe.
(a) Equivalent Length.
The loss of head in the pipe fittings are expression in terms of an equivalent length which is the length of uniform diameter pipe in which an equal loss of head and the same discharge.

The equivalent Length Lc is obtained by equating minor loss equal to major loss

The Equivalent length for a given pipe fitting can be expressed in terms of pipe diameter.
(b) Equivalent pipe.
It is defined as the pipe of uniform diameter having loss of head equal to the total loss of head as the compound pipe at same discharge (Q). The uniform diameter of the equivalent pipe is called equivalent size of the pipe. The length of equivalent pipe is equal to sum of length of the compound pipe as shown in figure 2.34.

Equivalent Length Le = L1 + L2 + L3
de = diameter of the equivalent pipe
Head loss in equivalent pipe = Sum of head loss in pipes in series.
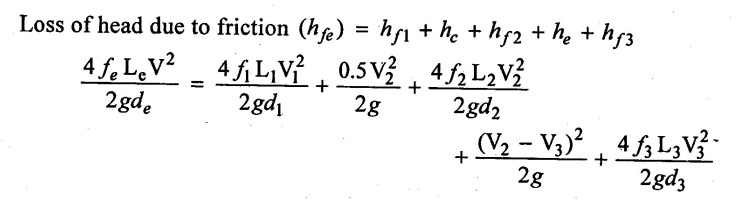
neglecting minor loss.
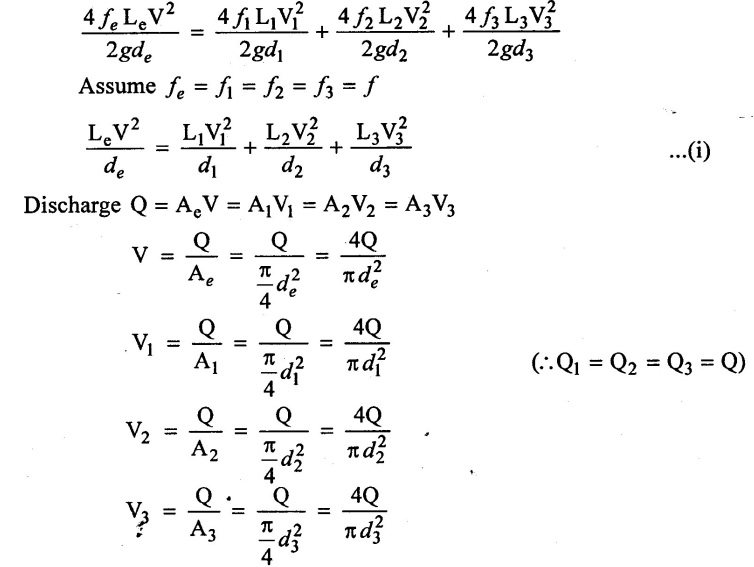
Substituting the values of V1, V2 and V3 in equation (i)

The above equation is called Dupuit's equation. In this equation Le = L1 + L2 + L3 and d1, d2 & d3 are known. Hence diameter of equivalent pipe (de) can be determined.
If the diameter of the equivalent pipe (de) is fixed up its length Le can be determined. In that case Le ≠ L1 + L2 + L3.
5. Power Transmission Through Pipes:
Power is transmitted through pipes when water is flowing through them. So hydraulic power can be produced. When water is flowing through hydraulic machines which is mounted at the outlet of the pipe.
Power is transmitted depends upon
(i) Weight of the water w in N/sec
(ii) Total head of water at the end of pipe in m
Power (p) = w + head at outlet
Total head at inlet (H)
Loss of head due to friction (hf)

6. Solved Examples based on Pipes in Series, Parallel, Equivalent Pipe and Power Transmission through pipes.
Example - 68
Two reservoirs are connected by a pipe line consisting of two pipes in series. One pipe diameter of 10 cm and 4m long and another pipe diameter of 18 cm and 10 m long. If the difference in water level of the reservoirs is 8m. Calculate discharge when considering all losses. Take f = 0.02 for both pipes.
Given Data:
Diameter of first pipe (d1) = 10cm = 0.1m
Length of first pipe (L1) = 4m
Diameter of second pipe (d2) = 18cm = 0.18m
Length of second pipe (L2) = 10m
Difference in water level (H) = 8m
Co-efficient of friction (f) = 0.02
To Find
Discharge (Q) when consider all losses.
Solution:
(i) Appying continuity equation.

(2) Head loss at entrance of the pipe
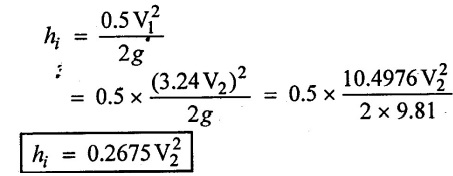
(3) Head loss due to friction in pipe (i)
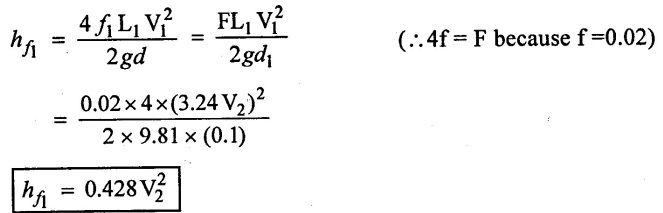
4) Loss of head at sudden enlargement
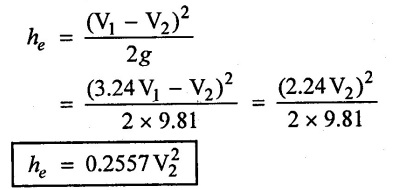
5) Loss os head due to friction pipe - 2
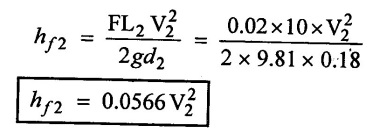
6) Loss of head at exit of the pipe (ho)
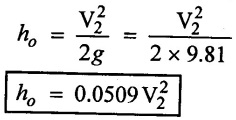
7) Pipes in series the total loss of head is equivalent to total head at inlet

8) Rate of discharge (Q)

Result
Discharge Q = 0.0699 m3/s
Example - 69
The difference in water surface levels in two which are connected by three pipes in series of lengths 400m, 310m and190m and diameters 400mm, 250mm, and 500mm respectively is 10m. Determine the rate of flow of water if co-efficient of friction are 0.004, 0.0058 and 0.003 respectively. consider (i) minor losses (ii) neglecting the minor losses.
Given data:
Difference of water level (H) = 10m
Length of first pipe L1 = 400m
Length of second pipe L2 = 310m
Length of third pipe L3 = 190m
Diameter of first pipe (d1) = 400mm = 0.4m
Diameter of second pipe (d2) = 250mm = 0.25m
Diameter of third pipe (d3) = 500mm = 0.5m
Co-efficient of friction at pipe -1 (f1) = 0.004
Co-efficient of friction at pipe 2 (f2) = 0.058
Co-efficient of friction at pipe (f3) = 0.003
To find
Rate of flow when (i) Consider all losses
(ii) Neglecting minolosses.
Solution:
(i) Apply Continuity equation

Case - (i)
(ii) Consider all the losses.
Total head (H) = major loss + minor loss

(iii) Discharge (Q) = A1 V1
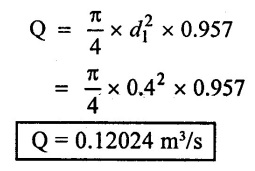
Case (ii)
(iv) Neglecting minor losses
Total head (H) = Major Loss due to friction.

(v) Rate of flow (Q)
Q = A1 V1
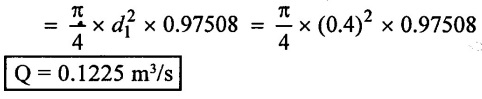
Result:
(i) Rate of flow
(ii) When consider all losses (Q) = 0.1204 m3/s
(ii) When neglecting minor losses (Q) = 0.1225 m3/s
Example - 70
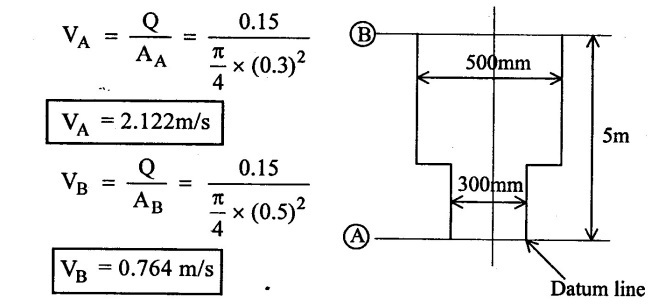
A pipe line carrying oil of specific gravity 0.8 changes in diameter from 300mm at a position A to 500mm diameter to a position B which is 5m at higher level. If the pressure at Aand B are 19.6 N/cm2 and 14.9 N/cm2 respectively for a discharge of 150 lps. Find the loss of head and direction of flow.
Given data.
Specific gravity (S) = 0.8
Diameter of pipe (A) (dA) = 300mm = 0.3m
Diameter of pipe (dB) = 500mm = 0.5m
Pressure at pipe (PA) = 19.6 N/cm2 = 19.6 × 104 N/m2
Pressure at pipe (B) (PB) = 14.9 N/cm2 = 14.9 × 104 N/m2
Discharge (Q) = 150 lit/sec = 0.15 m3/sec
To find:
(i) Loss of head (hf)
(ii) Disrection of flow
Solution:
(i) Rate of flow (Q) = AA × VA = AB × VB
(ii) Specific Gravity (S) = ρof oil / ρof water
ρof oil = S × ρof water = 0.8 × 1000
= 800 kg/m3
(iii) Assume the direction of flow from A to B
By using Bernoulli's Equation

We get positive value of hf. So the direction of flow is A to B.
Result:
(i) Loss of head (hf) = 1.19m
(ii) Direction of flow is pipe A to pipe (B)
Example - 71
A main pipe divides into two parallel pipes which again forms one pipe. the length and diameter for the first parallel pipe are 2000m and 1.5m respectively, When the length and diameters of 2nd parallel are 2000m and 1.0m. Find the rate of flow in each parallel pipe. If total flow in mains 3.0 m3/s. The co-efficient of friction is equation to 0.005.
Given Data:
L1 = 2000m
d1 = 1.5m
L2 = 2000m
d2 = 1.0m
Q = 3.0 m3/s
f1 = f2 = f = 0.005
To find.
Discharge in each parallel pipe Q1 & Q2
Solution
(i) Loss of head is equal in parallel pipes. (h f1 = h f2)

(ii) Rate of flow in pipe (1)
Q1 = A1 × V1
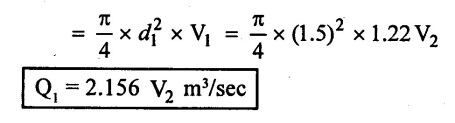
(iii) Rate of flow in pipe (2)
Q2 = A2 × V2

(iv) Total rate of flow (Q)
Q = Q1 + Q2 = (2.156 + 0.785) V2
Q = 2.941 V2
3.0 = 2.941 × V2
V2 = 3.0 / 2.941
V2 = 1.02 m/s
Q2 = 0.785 × V2 = 0.785 × 1.02
Q2 = 0.801 m3/sec
Q = Q1 + Q2
3.0 = Q1 + 0.801
3.0 - 0.801 = Q1
Q1 = 2.199 m3/sec
Result:
(i) Rate of flow in pipe (1) Q1 = 2.199 m3/sec
(ii) Rate of flow in pipe (2) Q2 - 0.801 m3/sec
Example - 72
A pipe line 0.5m diameter is 1.5km long to increase the discharge another line of the same diameter is introduced parallel to the first in the second half of the length. Neglecting minor losses, find increase in discharge if 4f = 0.04. The head at inlet is 300mm.
Given data:
Diameter of pipe line (D) = 0.5m
Length of pipe (L) = 1.5 km = 1500m

Diameter of the another pipe line (d1) = 0.5m.
To find.
(i) Discharge of a single pipe line
(ii) Discharge of parallel pipe line connected.
Solution:
Case(i) Discharge of single pipe line

Case (ii) Discharge of parallel pipe line connected.
(i) Total Rate of flow Q = Q1 + Q2
Q1 = Q2 = Q/2
(ii) From figure (ii)
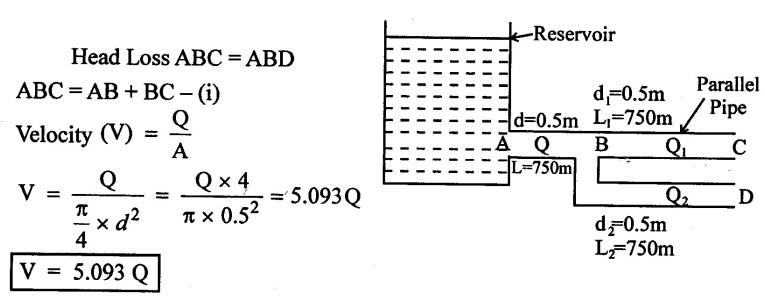
(iii) Loss of head due to friction at A to B
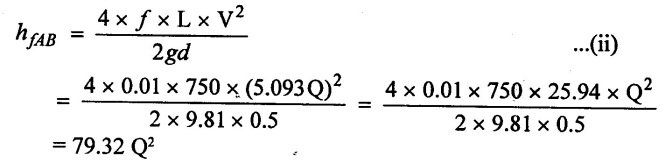
(iv) Loss of head due to friction at BC

(v) Loss of head AB and BC values apply in equation (i)
(hƒ)ABC = (hƒ)AB + (hƒ)BC
0.3 = (79.32 + 19.91) Q2
0.3 = 99.23 Q2
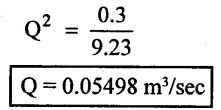
(vi) Increase discharge = Q - Q* = 0.05498 – 0.043
Q = 0.01198 m3/s
Result:
(i) Discharge in single pipe (Q*) = 0.043 m3/sec
(ii) Discharge of parallel pipe line (Q) = 0.05498 m3/sec
(iii) Increase of discharge = 0.01198 m3/sec
Example - 73
Two pipes of identical length and material are connected is parallel. The diameter of pipe A is 3 times the diameter of pipe B. Assuming the friction factor to be the same in both cases and disregarding minor losses determine the ratio of the flow rates in the two pipes.
Given Data
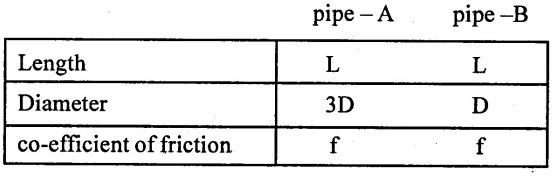
To find
Ratio of flow rates
Solution
(i) Loss of head due to friction in equal for parallel pipes
hfA = hfB
W.K.T
QA = AA × VA
VA = QA / AA
Similarly
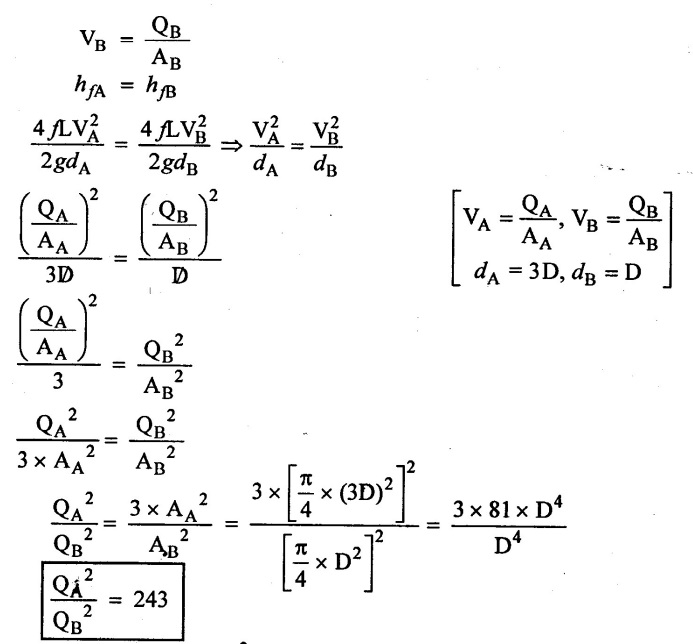
Result:
Ratio of flow rate is 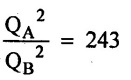
Example - 74
Two pipes of 15cm and 30cm diameters are laid in parallel to pass a total discharge of 100 lit/sec. Each pipe is 250m long. Determine discharge through each pipe. Now these pipes are connected in series to connect two tanks 500m a part, to carry same total discharge. Determine water level difference between the tanks. Neglect minor losses in both cases, f= 0.02 both pipes.
Given:
Case (i) Parallel pipe
d1 = 15cm = 0.15m
d2 = 30cm = 0.3m
L1 = L2 = 250m
Q = 100 lit/sec = 0.1 m3/s
f = 0.02
Case(ii) pipes in series
L = 500m
Q = 0.1 m3/s
f = 0.02
To find:
(i) Discharge in each pipes when pipes in parallel (Q1 & Q2).
(ii) Water level difference between the tanks when pipes in series (H).
Solution:
Case (I) pipe in parallel

(vi) Velocity value V2 apply in equation (ii)
Q1 = 0.0125 × V2 = 0.0125 × 1.203
Q1 = 0.016 m3/s
(vii) Velocity value apply in equation (iii)
Q2 = 0.0706 × V2 = 0.0706 × 1.203
Q2 = 0.0849 m3/s
Case(II) Pipes in series
(i) Total head (H) = sum of head losses in the two pipes (Neglect minor losses)
H = loss of head due to friction in pipe (1) hƒ1 +
Loss f head due to friction in pipe (2) hƒ2
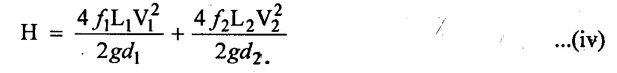
(ii) Total rate of flow (Q)
Q = A1 V1 = A2 V2
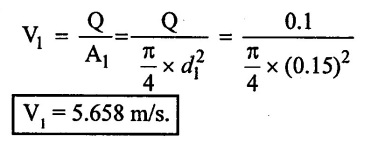
Similarly
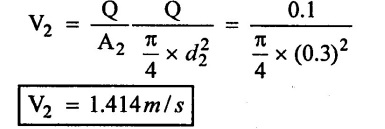
Apply the value of V1 & V2 in equal (iv)
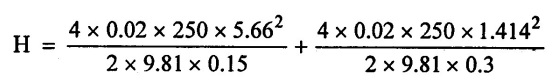
H = 224.4m
Result:
(i) Discharge Q1 = 0.016 m3/s, Q2 = 0.0849 m3/s
(ii) Water level difference between the tanks (H) = 224.4 m.
Example - 75
Three pipes of lengths 700m. 500m and 200m and of diameter 50cm, 40cm and 30cm respectively are connected in series. these pipes are to be replaced by a single pipe of uniform diameter (equivalent pipe). Find the length and dia of equivalent pipe
Given Data
Length of pipe - (L1) = 700m
Length of pipe - 2 (L2) = 500m
Length of pipe -3 (L3) = 200m
Diameter of pipe - 1 (d1) = 50cm = 0.5m
Diameter of pipe - 2 (d2) = 40cm = 0.4m
Diameter of pipe - 3 (d3) = 30 cm = 0.3m
To find.
(i) Equivalent length of series pipe (Le)
(ii) Equivalent diameter of series pipe (de)
Solution

Result:
(i) Equivalent length of series pipe (Le) = 1400m
(ii) Equivalent diameter of series pipe (de) = 0.391m
Example - 76
A compound piping system consists of 1600m of 0.5m, 1000m of 0.4m and 400m of 0.3m. New Cast Iron are connected in series convert the system to (i) equivalent length of 0.4m diameter pipe (ii) equivalent size of 3600m length.
Given data:
Length of pipe - (1) = 1600m
Length of pipe - (2) = 1000m
Length of pipe - (3) = 400m
Diameter of pipe (1) = 0.5m
Diameter of pipe (2) = 0.4m
Diameter of pipe (3) = 0.3m
Equivalent diameter = 0.4m
Equivalent length = 3600m
To find
(i) Equivalent diameter when Le = 3600m
(ii) Equivalent length when de = 0.4m.
Solution
Case (i)
Equivalent diameter when Le = 3600m

Case(ii)
Equivalent length when de = 0.4m.

Result
(i) Equivalent diameter when Le is 3600m = 0.41m
(ii) Equivalent length when de is 0.4m = 3209.88m
Example - 77
A 40cm diameter pipe conveys water for power generation - The pipe is 800m long and head of 80m at inlet. When maximum power can be generates from system? and Also find Efficiency. Take f = 0.006
Given data:
Diameter of pipe (d) = 0.4m
Length of pipe (L) = -800m
Head (H) = 80m
Co-efficient of friction (f) = 0.006
To find
(i) Maximum power generation
(ii) Efficiency
Solution

Result:
(i) Power generation (P) = 217.114 kw
(ii) Efficiency (η) = 66.67%
Example - 78
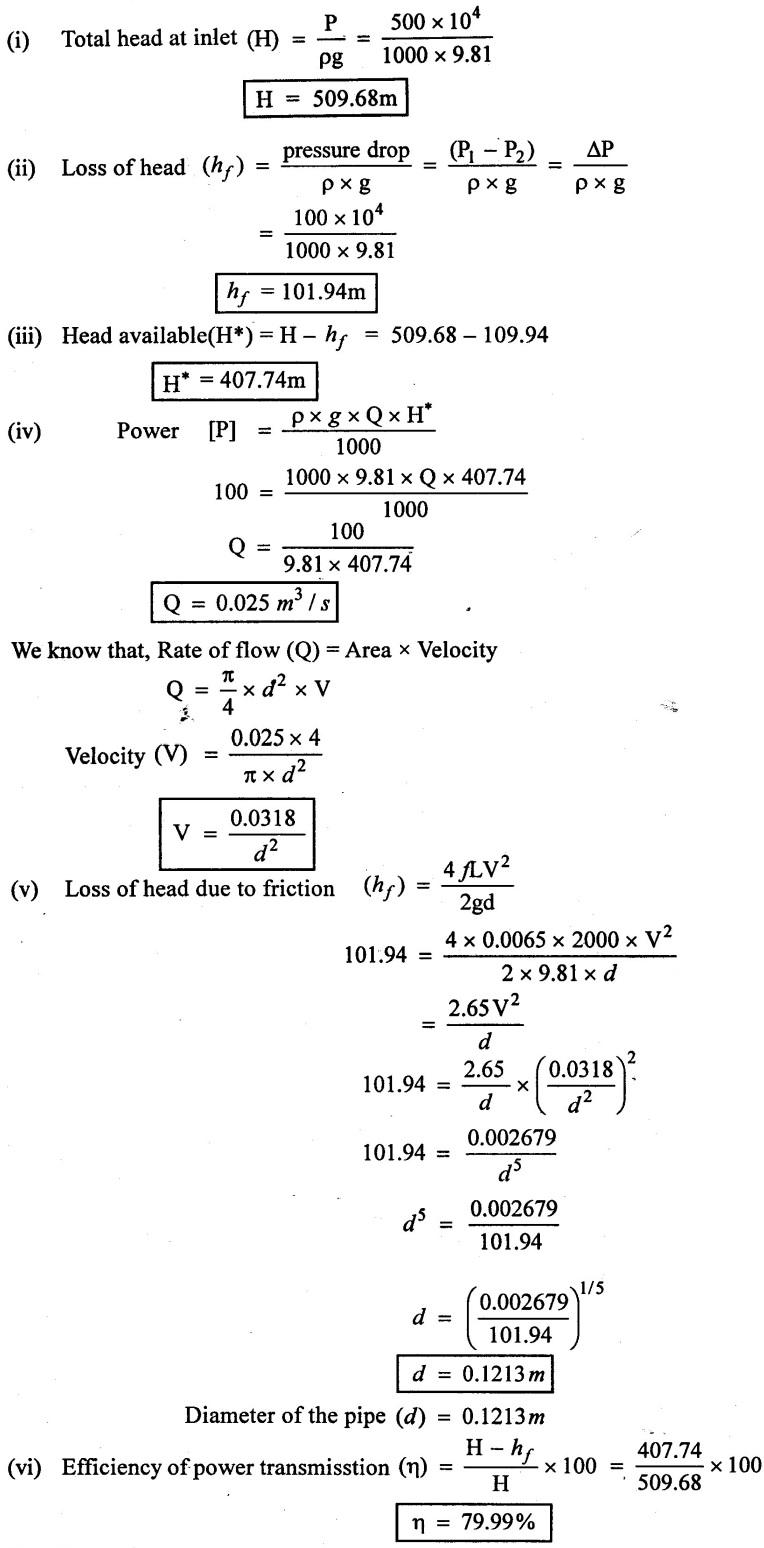
A pipe line of length 2000m issued for power transmission. If 100 kw Power is to be transmitted through the pipe in which water having pressure of 500 N/ cm2 at inlet is flowing. Find the diameter and efficiency of power transmission if the pressure drop over length of the pipe is 100 N/cm2. Take f = 0.0065
Given data:
Length of pipe line (L) = 2000m.
Power (P) = 100kw = 100 × 103 watts
Pressure at Inlet (P) = 500 N/cm2 = 500 × 104 N/m2
Pressure drop (AP) = 100 N/cm2 = 100 × 104 N/m2
f = 0.0065
To find
(i) Diameter of pipe (d)
(ii) Efficiency of power transmission (η)
Solution
Result:
(i) Diameter of the pipe (d) = 0.1213 m
(ii) Efficiency of power transmission (η) = 79.99%
Example - 79
Determine the length of a equivalent pipe of diameter 10cm and friction factor 0.03 for a given pipe system discharging 0.3 m3/s. The pipe system consists of the following
(i) A 15 m line of 10cm diameter with f = 0.02
(ii) three 90° bend, K= 0.6 for each
(iii) Two sudden expansion of diameter 10cm to 20cm.
(iv) A20m line of 20cm diameter with ƒ = 0.028 and
(v) A global value. fully open K = 9
Given data:
Equivalent pipe diameter (de) = 10cm = 0.1m
Friction factor of Equivalent pipe (Fe) = 0.03
First pipe length in pipe line (L1) = 15m
First pipe diameter in pipe line (d1) = 10cm = 0.1m
First pipe friction factor (F1) = 0.02
pipe bend (θ) = 90°
Co-efficient of friction of pipe bend (Kb) = 0.5
No. of bend = 3
Sudden expansion pipe diameter (d2) = 20cm = 0.2m
Second pipe diameter (d2) = 20cm = 0.2m
Length of second pipe (L2) = 20m
Valve co-efficient of friction (kv) = 9
Discharge (Q) = 0.3 m3/sec
To find
Equivalent length of pipe diameter in the pipe line
Solution
(i) Loss of head due to friction in first pipe

(ii) Loss of head due to bend (hb)

(iii) Loss of head due to expansion (Le)

he = 41.88 m/s
Total loss of head due to expansion he = 2 × 41.88
= 83.76 m
(iv) Loss of head due to friction in pipe
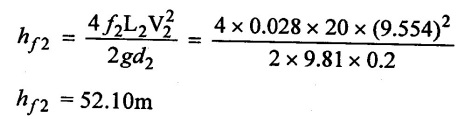
(v) Loss of head due to Global valve if kv = 9

(vi) Equivalent length of equivalent pipe
Loss of head in equivalent pipe = Total loss of head in pipe line system

Result
Equivalent length of pipe diameter in pipe line is 168.25m
Example - 80
Water flow through a pipe 200m diameter at the rate of 0.5m3/s. The straight length of pipe is 70m and one open global valve. A T-joint through outlet and elbow is provided in it. If the values of K for these fittings are 5, 2.1 and 0.6 respectively. What is the total length of the pipe loss of head in it? Take ƒ for the pipe is 0.028
Given data:
Diameter of the pipe (d) = 200mm = 0.2m
Discharge (Q) = 0.5m3/s
Length of pipe (L) = 70m
Co-efficient of friction of Global valve kv = 5
Co-efficient of friction of T - joint kT = 2.1
Co-efficient of friction of Elbow kE = 0.6
Co-efficient of friction of pipe f1 = 0.028
To find
Equivalent length of pipe (Le)
Solution

(5) Loss of head due to T - Joints fitting
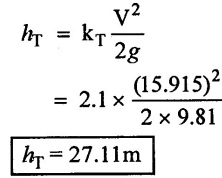
(6) Loss of head due to elbow fitting
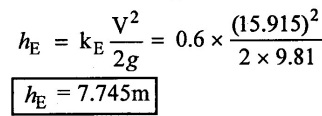
(7) Total loss of head (h) = major loss + minor loss
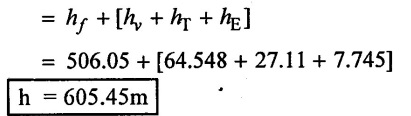
(8) Equivalent of pipe has same head loss
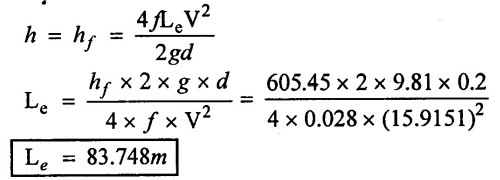
Result:
Equivalent length of pipe (Le) = 83.748m
Example - 81
Two reservoir at different elevations are connected with a compound pipe of 0.5 km total length consisting of two sections. First section connect to higher level reservoir is 250m long and 100mm in a diameter and other half is connected to lower level reservoir and has 50mm diameter. Darcy weisbatch friction factors for the pipes are 0.012 and 0.01 respectively. If velocity of flow of water in the second section is Imls. Find the difference in water levels in the reservoirs considering all losses. Find the rate of flow of water also find diameter of single uniform diameter pipe replace the above pipe line to carry same discharge.
Given data:
Total length (L) = 0.5 km = 500m
Diameter of pipe (1) d1 = 100mm = 0.1m
Length of pipe (1) (L1) = 250m
diameter of pipe (2) (d2) = 50mm = 0.05m
Length of pipe (2) (L2) = 250m
Co-efficient of friction at pipe (1) f1 = 0.012
Co-efficient of friction at pipe (2) f2 = 0.01
Velocity of pipe at 2 (V2) = 1 m/s
To find
(i) Total head loss when pipes in series
(ii) Discharge of flow when pipes in series
(iii) Equivalent diameter when pipe consider equivalent length.
Solution:

(v) minor loss = Loss at entry + due to contraction + Loss at exit
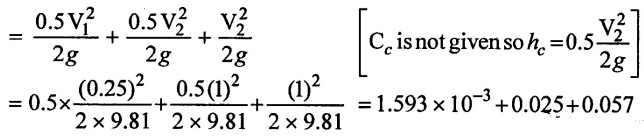
= 0.07756m
(vi) Total head loss (H) = 10.575 + 0.07756

(vii) Equivalent diameter when consider equivalent length.
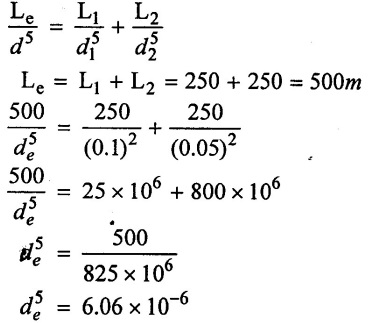
Equivalent diameter (de) = 0.057m
Result:
(i) Total head loss (H) = 10.653m
(ii) Discharge of flow (Q) = 1.963 × 10-3 m3/sec
(iii) Equivalent diameter (de) = 0.057m
Example - 82
Two reservoir are connected by three pipes in parallel their diameter are d, 2d, 3d having same frictional factor of pipes. Determine the discharge through larger pipes if discharge through smaller pipe is 2 m3/sec.
Given data:
diameter of pipe (1) = (d1) = d
diameter of pipe (2) = (d2) = 2d
diameter of pipe (3) (d3) = 3d
discharge though pipe (1) = Q1 = 2 m3/sec
discharge through pipe (2) = Q2
To find
Discharge through large pipes Q2 & Q3.
Solution:
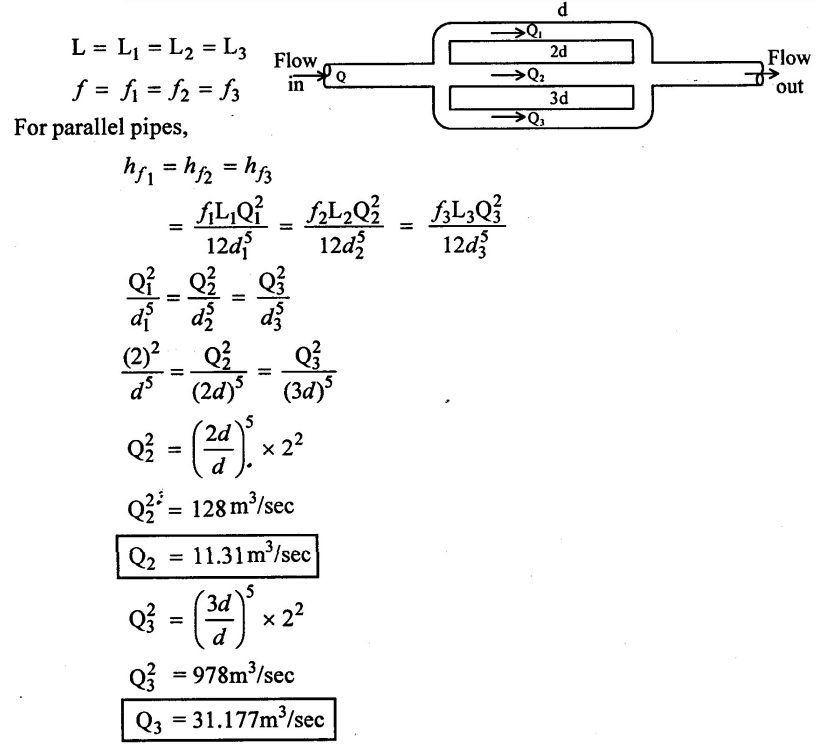
Result
Discharge at pipes 2 & 3 are 11.31m3/sec and 31.177m3/sec respectively.
Example - 83
Two reservoirs whose water surface elevation differ by 50m are connected by a pipe line 40cm in diameter and2.5km long. In order to increase be the discharge, an additional pipe line 15cm in diameter and 1.25 km long is laid parallel from the mid-point of the first one up to the lower reservoir. What is the increase in discharge due to the newly laid pipe? Assume friction factor (f) = 0.92. Neglect minor losses.
Given data:
H = 50m
diameter of pipe d = 40cm = 0.4m
Length of pipe L = 2.5 km = 2500m
friction factor (f) = 0.92
Diameter of additional pipe d2 = 15cm = 0.15m
Length of additional pipe L2 = L3 = 1250 m
To find
Increase in discherge
Solution:
Case(i) Two reservoir are connected by a single pipe
To load (H) = Loss of head due to friction (hf)

Case(ii) To increase discharge additional pipe DE is laid parallel from mid point to lower reservoir

W.K.T
(ii) Pipe in parallel Q1 = Q2 + Q3
= 11.61 × Q3 + Q3
Q1 = 12.61Q3
(iii) Head loss (H) = hƒ1 + hƒ3

(iv) ⸫ Increase in discharge = Q1 – Q
= 0.1075 – 0.0106
= 0.0969 m3/s
Result:
Increase in discharge is = 0.0969 m3/s.
Example - 84
Two similar pipes of the same diameter of length l1 &l2 are placed in parallel. Calculate the equivalent length of a single pipe of the same diameter. What would be the equivalent length if the two pipes were equal in length?
Solution:

Result:
Equivalent length = L/4
Example - 85
Pipes of 50cm diameter 1800m length, 40cm diameter 1200m length, 30cm diameter 600m length are connected in series.
(i) If these pipes are to be replaced by an equivalent pipe of 40cm diameter, what would be its length?
(ii) What would be the diameter of the equivalent pipe of 3600m length
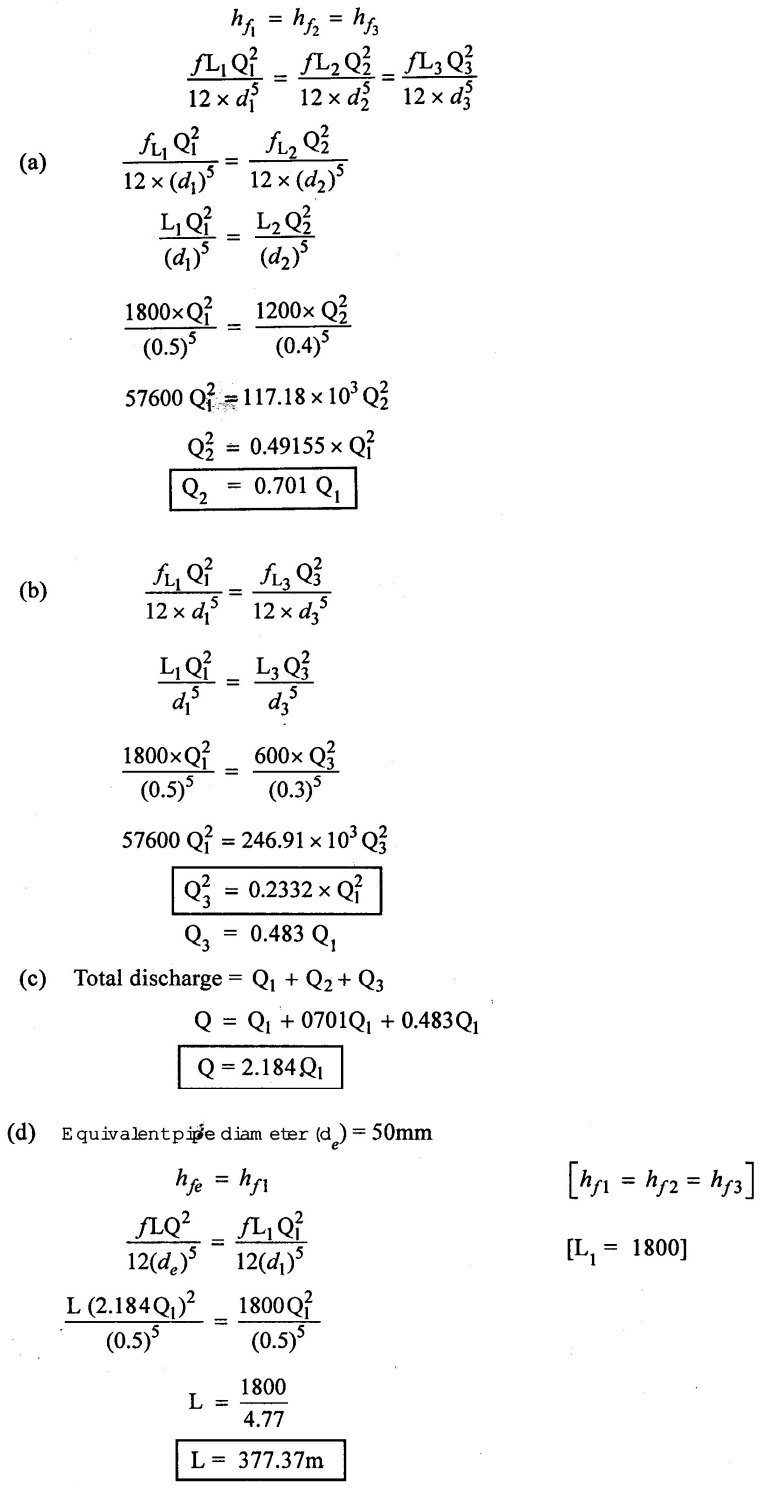
(iii) If the three pipes are connected in parallel, what is the equivalent length of 50cm diameter pipe?
Given data:
Length of pipe - I (L1) = 1800m
Length of pipe II (L2) = 1200m
Length of pipe III (L3) = 600m
Diameter of pipe I (d1) = 50cm = 0.5m
Diameter of pipe II (d2) = 40cm = 0.4m
Diameter of pipe III (d3) = 30 cm = 0.3m
Solution:
Case(i) length of equivalent pipe, If D = 40cm = 0.4m by Dupuits equation.
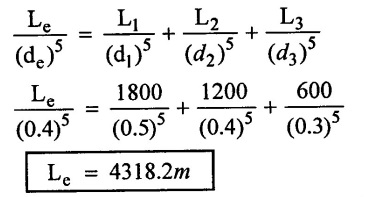
Case (ii) Diameter of equivalent pipe If Le = 3600m
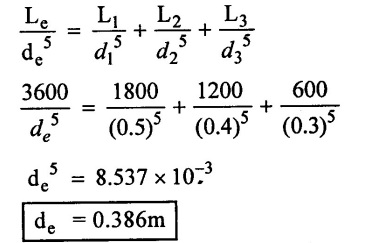
Case (iii) Three pipes are placed parallel,
Pipes are connected in parallel head loss are same in each pipe
Result:
(i) Length of equivalent pipe if d = 40cm. is Le = 4318.2m
(ii) Diameter of equivalent pipe if Le = 3600m
de = 0.386m
(iii) Equivalent length of pipe = 377.37m
No comments:
Post a Comment