Problem: 1
A centrifugal pump has an impeller 500mm in diameter at outlet and running at 400 rpm. The discharge of the inlet is enters radial. The velocity of flow at outlet is 1 m/s the vanes are curved backwards at outlet is 30o to the wheel tangent. If discharge of the pump is 0.14 m3/s. Calculate the impeller power and the torque on the shaft.
This problem is same as Example No.20 and page No: 4.92.
Ans:
Torque (T) = 305.8965 N.m
Power (P) = 12.8133 × 103w
Problem: 2
The dimensionless specific speed of a centrifugal pump is 0.06. Static head is 32 m. Flow rate is 50 l/s. The suction and delivery pipes are each of diameter 15 cm. The friction factor is 0.02. Total length is 60 m other losses equal to 4 times the velocity head in the pipe. The vanes are forward curved at 120°. The width is one tenth of the diameter. There is a 7 % reduction in flow area due to the blade thickness. The manometric efficiency is 80 %. Determine the impeller diameter if inlet is radial.
Given data:
Specific speed = 0.06
Static head = 32m
Discharge (Q) = 50 l/s = 50 × 10-3 m3/s
Diameter of suction and deliver pipe (ds) = (dd) = d = 15cm
Friction factor (F) = 0.02
Total length (ls, (or) ld) = 1 = 60m
Vane angles (θ) = 180° - 120° = 60°
Width at out let (B2) = 1/10 D2
Manometric efficiency = 80%
Flow over deduction = 7%
To find:
Impellet diameter (D2)
Solution:
(1) Discharge (Q) = Area of the pipe × Velocity (V)
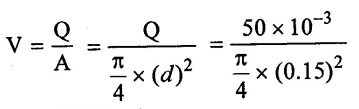
Velocity (V) = 2.829 m/s
(2) Total head (h) = hs + hfd
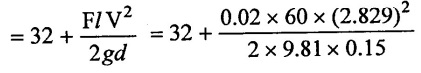
= 32 + 3.263
h = 35.263 m
(3) Manometric head (Hm) = Total head - Loss of the head
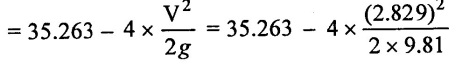
= 35.263 – 0.4079
Hm = 34.58 m
(8) From outlet velocity triangle
Result:
Impeller diameter (D2) = 5.0001 × 10-5 m
Problem: 3
A centrifugal pump is running at 920 rpm and delivering 0.32 m3/s of water against a head of 28 m, the flow velocity being 3 m/s. If the manometic efficiency is 80 % determine the diameter and width of the impeller. The blade angle of outlet is 25°
This problem is similar to Example No-17 and page No: 4.88.
Ans:
Diameter D2 = 0.324m
Width B2 = 0.0786m
Problem: 4
A centrifugal pump delivers 0.18 m3/s of water against a head of 10 m and runs at 620 rpm. The outlet and inner diameters of impeller are 0.4 m and 0.2 m respectively. And the vanes are bend back of 38° to the tangent at exit. If the area of flow remain of 0.1 m2 from inlet to outlet. Calculate manometric efficiency and Vane angle of inlet and loss of head at inlet to impeller when the discharge is reduced by 40% without changing the speed.
Given data:
Discharge (Q) = 0.18 m3/s
Manometric head (Hm) = 10m
Speed (N) = 620 rpm
Outlet impeller diameter (D2) = 0.4m
Innet impeller diameter (D1) = 0.2m
Area of flow (Af) = 0.1m2
Outlet vane angle (ϕ) = 38°
To find:
(i) Manometric efficiency
(ii) Inlet vane angle (θ)
(iii) Loss of head at inlet to impeller when discharge is reduced by 40%.
Solution:
Result :
1. Manometric efficiency ηmano = 70.79%
2. Inlet vane angle (θ) = 15.49
3. Loss of head at impeller = -0.385 m
Problem: 5
The internal and external diameter of impeller of a centrifugal pump which is running of 1000 rpm, are 200 mm and 400mm respectively. The dischage through the pump is 0.04 m3/s, and velocity of flow is constant and equal to 2.0 m/s. The diameters of the suctionand delivery pipes are 150mm and 100 mm respectively. If the outlet vane angle is 45o and power required to drive the pump is 16.186 kw determine.
(i) Vane angle of impeller of inlet
(ii) The overall efficiency
(iii) Manometric efficiency
This problem, is similar to Example No: 6 and Page No: 4.64.
Ans:
(i) Vane angle of inlet θ = 10°.48′
(ii) Overall efficiency (ηo) = 60.74%
(iii) Manometric efficiency (ηmano) = 61.98%
Problem: 6
The internal and external diameters of the impeller of centrifuged pump are 300mm and 600mm respectively. The pump is running of 1000 rpm. The vane angles of the impeller at inlet and outlet are 20° and 30° respectively. The water enters the impellet radially and velocity of flow is constant. Determine the workdone by the impellet per unit weight of water. Sketch the velocity triangle.
Given data:
Internal dia of impeller (D1) = 300 mm = 0.3 mm
External dia of impeller (D2) = 600 mm = 0.6 mm
Speed (N) = 1000 rpm
Vane angle at inlet (θ) = 20°
Vane angle at outlet (ϕ) = 30°
Radial flow of water at inlet
(i.e) α = 90°, Vwj = 0
Velocity of flow is constant Vf1 = Vƒ2
To find:
Workdone by impeller per unit weight of water
Solution:
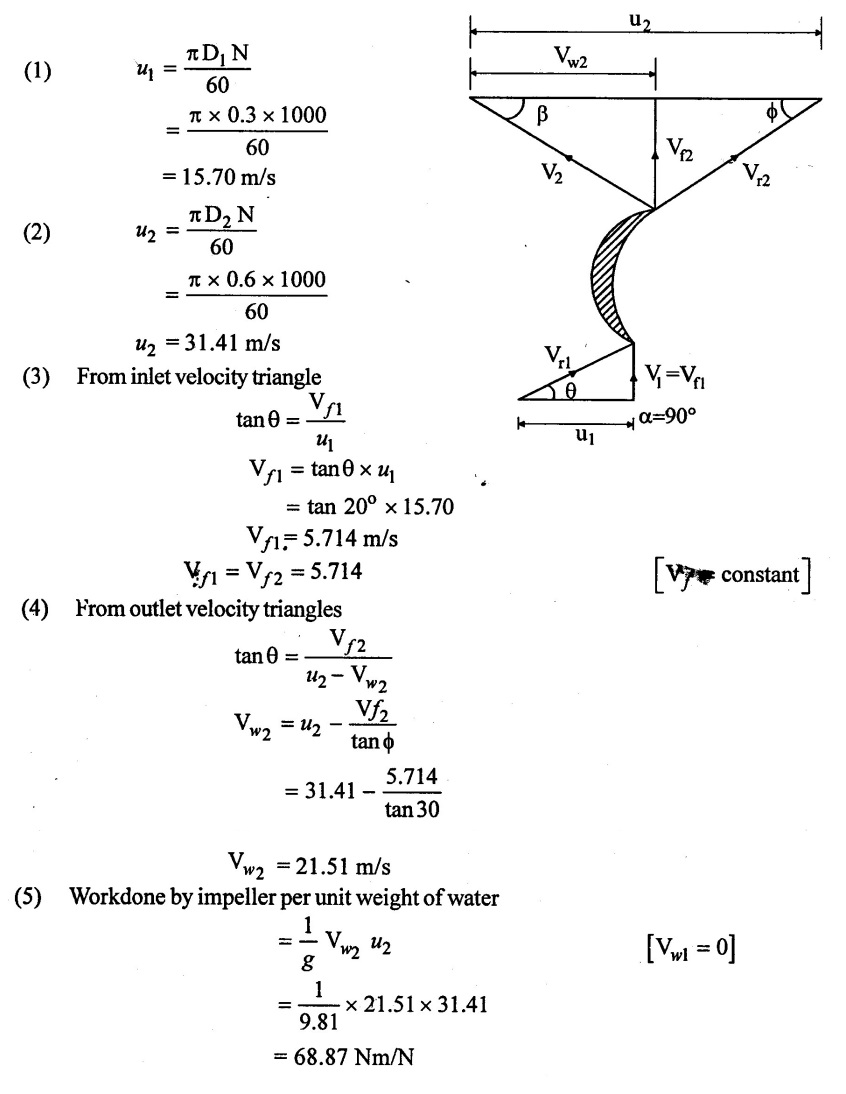
Result:
Workdone by impeller /unit weight of water = 68.87 Nm/N
Problem: 7
A centrifugal pump has a head discharge given by H=35-2200. Q2, where H is gead by pump in 'm' and Q is discharge is m3/s. The pump is to deliver a discharge against a static head of 12m. The suction pipe is 15 cm diameter and 20m long with an f value of 0.018. The delivery pipe is 20 cm diameter and 40m long with an f value 0.02. Calculated the head and discharge delivered by the pump. If the overall efficiency is 0.7, also calculate the power supplied.
Given data:
Head (H) = 35 - 2200 Q2
Static head (Hs) = (hs + hd) = 12m
Diameter of suction pipe (dş) = 15cm = 0.15m
Length of suction pipe (ls) = 20m
Diameter of delivery pipe (dd) = 20 cm = 0.2 m
Length of delivery pipe (ld) = 40 m
Friction factor of suction pipe (Fs) = 0.018
Friction factor of delivery pipe (Fd) = 0.02
Overall efficiency (ηo) = 0.7
To find:
(i) Total Head (H)
(ii) Discharge (Q)
(iii) Power supplied (P)
Solution:
Result:
Discharge (Q) = 0.0898 m3/s
Total head (H) = 17.245 m
Power (P) = 21.702 × 103w
Problem: 8
The internal and external diameter of the impeller of a centrifuged pump are 200mm and 400 mm respectively. The pump is running at 1200 rpm. The vane angle of the impeller at inlet and outlet are 20° and 30° respectively. The water enters the impeller radially and the velocity of flow is constant. Determine workdone by the impeller per unit weight of water.
This problem is similar to previous university solved problems No: 6 Page No: 4.163.
Ans:
Work done by impellet/unit weight of water = 45.9839 Nm/N.
Problem: 9
A centrifugal pump impeller has a outlet diameter of 360 mm and width 60mm. The vanes are curved backwards at 35o to the tangent at outer periphery and thickness of vanes occupy 20% of the peripheral area. Velocity of flow is constant from inlet to outlet. The impeller rotates at 800 rpm. If the take of flow through the pump is 0.13 m3/s. Determine
(i) The pressure rise in the impeller and
(ii) The percentage of total work converted to kinetic energy
This problem is similar to Example No:10 and Page No: 4.73.
Ans:
1. Pressure rise in the impellet = 10.99 m of water
2. % of total work converted in to kinetic energy = 40.29%
Problem: 10
Show that the pressure rise across the impeller of a centrfual pump is given by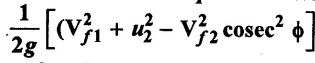 
. Where Vƒ1 and Vƒ2 are velocities of flow of inlet and outlet. V2 = tangential velocity of impellet of outlet, ϕ = vane angle of outlet
Solution:
Applying Bernoulli's equation at the inlet and outlet of the pump impeller we get,
Total energy at inlet = Total energy at outlet - Workdone by impeller.
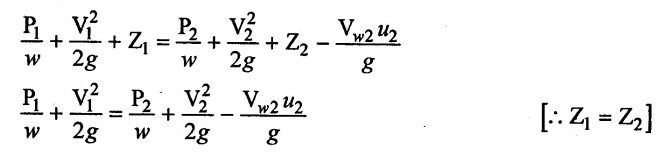
Now the pressure rise in impeller is,
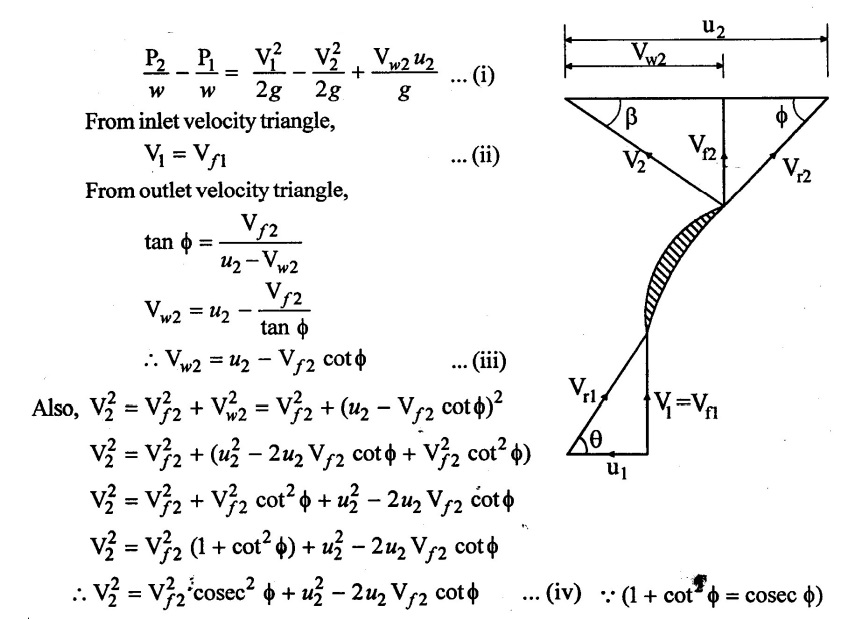
Substituting the values of equation (ii), (iii) & (iv) in equation (i)
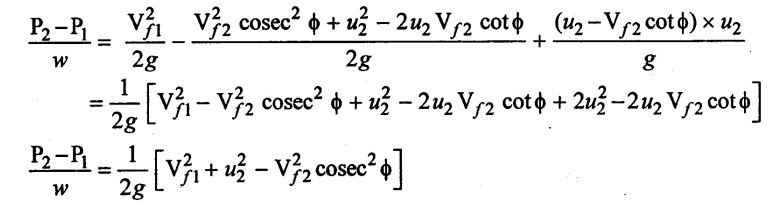
⸫ Hence proved.
Problem: 11
It is required to deliver 0.05 m3/s of water to height of 25 m through a 150mm diameter pipe and 120m long, by a centrifugal pump. If the over all efficiency of the pump is 80 % and co-efficient of friction = 0.01 for the pipe line, find the power required to drive the pump.
This problem is similar to Example No:7 and Page No: 4.67.
Ans:
Power (P) = 23.5837 × 103 watts
Problem: 12
A centrifugal pump delivers 1565 LPS against a manometric head of 6.1m. When the impeller rotates at 200 rpm. The impeller diameter is 1.22m and the area at outlet periphery is 6450 cm2. If the vanes are set back at an angle of 26° at the outlet determine.
1) Manometric efficiency
2) Power required to drive the pump
3) Minimum starting speed it ratio of external to internal diameter is 2.
This problem is same as Example No: 18 and Page No: 4.89.
Ans:
(i) ηmano = 60.04%
(ii) Power (P) = 155.9741 Kw
(iii) Minimum starting speed (Nmin) = 195.5245 rpm
Problem :13
A centrifugal pump has delivered water against a net head of 14.5m and a design speed of 1000 rpm. The vanes are curved back to angle of 30° with the periphery. The impeller diameter is 300mm and outlet width 50mm. Determine discharge of the pump if manometric efficiency is 95%
This problem is similar to Example No:4 and Page No: 4.61.
Ans:
Discharge (Q) = 0.1680 m3/s
Problem: 14
A centrifugal pump having outlet diameter equal to two times the inner diameter and running of 1200 rpm. Works against a total head of 75 m. The velocity of flow through the impeller is constant and equal to 3 m/s. The vanes are set back at width at an angle of 30° at outlet. If the outlet diameter is 600 mm and width ai outlet is 50mm, determine,
(i) Vane angle at inlet
(ii) Work done per second by impeller
(iii) Manometric efficiency
This problem is similar to Example No:3 and Page No: 4.59.
Ans:
1. Inlet angle θ = 9.0430°
2. ηmano = 60.04%
3. Work done/sec = 346.4008 × 103 Nm/s (or) Watts.
Problem :15
The impeller of a centrifugal pump has an external diameter of 450mm and internal of 200mm and it runs at 1440 rpm. Assuming a constant radial flow through the impeller at 2.5 m/s and that the vanes at exit are set back at a angle of 25o. Determine
(1)_Inlet vane angle
(2) The angle absolute velocity of water at exit makes with the tangent and
(3) The work done per N of water
This problem is similar to Example No: 4 and Page No: 4.61.
Ans:
θ = 9.4°
β = 5.0°
W = 98.7 N.m
Problem:16
A centrifugal pump impeller runs of 80 rpm and has outlet vane angle of 60°. The velocity of flow is 2.5m/s throughout and diameter of the impeller at exit is twice that inlet. If the manometric has is 20m and manometric efficiency is 75% determine the diameter of the impeller of the exit and the inlet vane angle.
This problem is same as Example No: 5 and Page No: 4.62.
Ans:
θ = 16.47°, D2 = 4.037 m
Problem: 17
A pump has to supply water which is at 70°c water at 90 m3/min and 1800 rpm. Find the type of pump needed, the power required and the impeller diameter, if the required pressure ries for one stage is 200 kpa and 1250 kpa.
Given data:
Discharge (Q) = 90m3/min = 1.5m3/s
Speed (N) = 1800 rpm
Pressure at inlet P1 = 200 kpa = 200 × 103N/m3
Pressure at outlet P2 = 1250 kpa = 1250 × 103 N/m2
To find:
(1) Type of pump needed
(2) Power required
Solution:
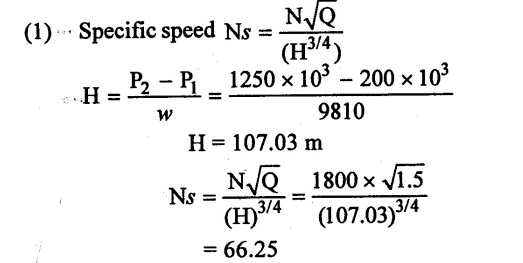
Specific speed lines between 50 to 80. So high speed radial flow pump is recommended.
Power (P) = w QH
= 9810 × 1.5 × 107.03
= 1.574 × 106w
Result:
Power (P) = 1.574 × 106w
Problem: 18
A single acting reciprocating pump running of 60 rpm. Delivers 0.02m3/s of water. The diameter of the piston is 250mm and stroke length 450mm. Determine(1) Theoretical discharge of the pump. (2) Co-efficient of discharge (3) Slip of the pump and (4)% slip of the pump.
This problem is similar to Example No: 21 and Page No: 4.122.
Ans:
(i) Qth =0.0221 m3/s
(ii) Cd = 1.105
(iii) Slip = 2.1 × 10−3
(iv) % of slip = 9.50%
Problem: 19
The plunger diameter and stroke length of a single acting reciprocating pump are 300mm and 50mm respectively. The speed of the pump is 50 rpm. The diameter and length of delivery pipe are 150mm and 55mm respectively. If the pump is equipped with an air vessel on the delivery side at the centre line of the pump. Find the power saved in over coming friction in the delivery pipe. Take friction co-efficient ƒ = 0.01
This problem is same as Example No: 34 and Page No: 4.143.
Ans:
Power saved (P) = 0.8337 kW
Problem: 20
Determine the maximum speed in rpm at which a single acting reciprocating pump without an air vessel of the following details can be operated without casing separation at any stage during the operation of the pump. Compute the discharge at this speed what would be the speed and discharge is air vessel is suited near the pump on the suction side?. The fluid is water. Assume ƒ = 0.01 for the pies. Diameter of plunger = 15 cm, static suction head=40m. Static delivery head=25m, atmospheric pressure = 101 kpa and vapour pressure of water = 25.5 kpa (abs).
This problem same as Example No: 36 and Page No: 4.147.
Ans:
(i) N = 16.1644 rpm
(ii) Q = 1.0712 × 10-3m3/s
Problem: 21
The cylinder of a single-acting reciprocating pump is 15cm in diameter and 30cm in stroke. The pump is running at 30 rpm and discharge of water to a height of 12m. The diameter and length of the delivery pipe are 10cm and 30m respectively.If a large air vessel is fitted in the delivery pipe at a discharge of 2m flow the centre of the pump. Find the pressure head in the cylinder.
(i) At the beginning of the delivery stroke and
(ii) In the middle of the delivery stroke take f = 0.01
This problem is same as Example No: 33 and Page No: 4.141.
Problem: 22
A single acting pump has a plunger 10cm diameter and a stroke length 200mm. The centre of the pump is 4m above the water level in the sump and is 14m below the water level in the over head water tank. The diameter and the length of the suction pipe are 40mm and 6m while that of the delivery pipe are 30mm and 18m respectively. Determine the maximum speed at which the pump can run without separation occurs of 7.848 N/cm2 below the atmospheric pressure. Take the atmospheric pressure head of 10.3m of water.
Given data
Plugenr diameter (D) = 10cm = 0.1m
Stroke length (L) = 200 mm = 0.2 m
Suction head (hs) = 4m
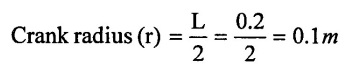
Delivery head (hd) = 14m
Diameter of suction pipe (ds) = 40mm = 0.04m
Length of suction pipe (ls) = 6m
Diameter of delivery pipe (dd) = 30mm = 0.03 m
Length of delivery pipe (ld) = 8 m
Separation pressure Psep = 7.848 Ncm2 = 7.848 × 104 N/m2
Separation head hsep =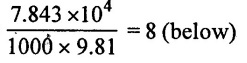 
Atmospheric pressur head = 10.3 m of water
To find:
Maximum speed of which pump way be operted with out separtion N
Solution:
6) Separation pressure head hsep = Absolute pressure head in beginning of suction stroke
The separation occurs in the suction stroke beginning only θ = 0.
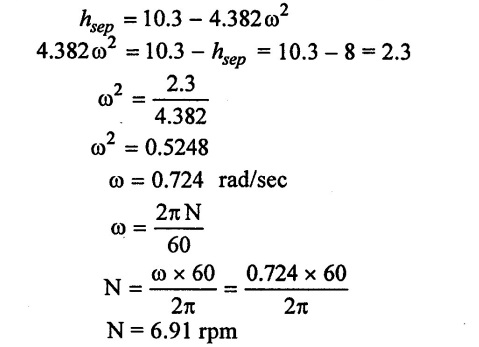
7) Acceleration head at end of delivery stroke θ = 0.
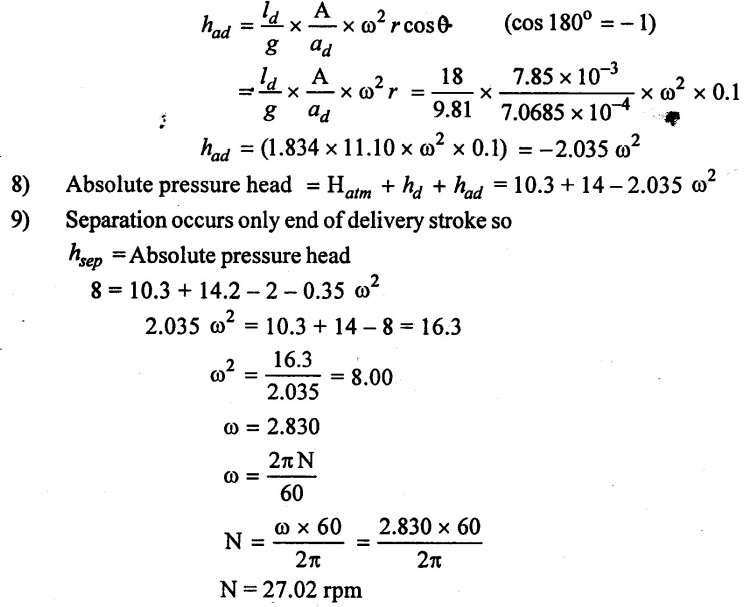
Result:
Maximum speed (N) = 27.02 rpm
Problem: 23
A double acting reciprocating pump has the following data, cylinder diameter = 10 cm, stroke = 15cm, speed = 60 rpm, suction head=3 cm, suction pipe is of 5 cm diameter and 4m length calculate the absolute pressure in m of water and in kg/cm2 in the cylinder of the (i) Beginning (ii) middle (iii) end of suction stroke Assuming f = 0.01
Given data:
Cylinder diameter (D) = 10 cm = 0.1 m
Stroke length (L) = 15 cm = 0.15 m
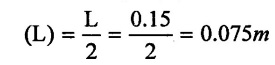
Speed (N) = 60 rpm
Suction head = (hs) = 3
Suction pipe diameter (ds) = 5 cm = 0.05 m
Length of suction pipe (ls) = 4 m
Friction facctor (f) = 0.01
To find:
Absolute pressure in the suction stroke when
(i) Beginning
(ii) Middle
(iii) end of the stroke
Solution:
6) Absolute pressure head beginning of suction stroke (θ = 0°)
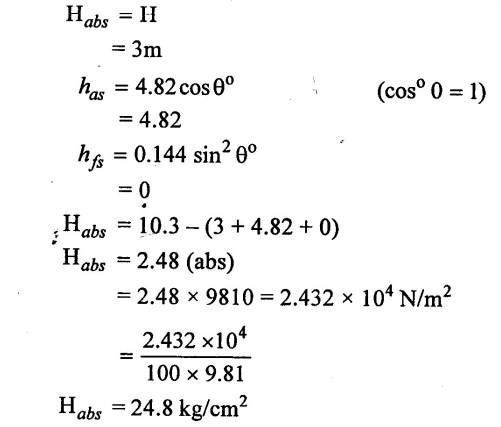
(7) Absolute head middle of suction stroke
θ = 90°
Problem: 24
A single acting reciprocating pump has a piston area of 0.185 m2 and stroke as 0.3 m. Cross section area of the delivery pipe is 0.37 m2 and water is lifted to a height of 12m. Find % of slip, co-efficient of discharge and theoretical HP required to derive the pump if it is running at 60 rpm and actual discharge is 50 lit/sec
This problem is similar to Example No: 22 and Page No: 4.124.
Ans:
(i) % of slip = 9.909 %
(ii) Cd = 0.909
(iii) Pth = 8.76HP
Problem: 25
A cylinder bore diameter of a single acting reciprocation pump is 150mm and its stroke is 300mm. The pump runs at 50 rpm and lifts water to a height of 25m. The delivery pipe is 22m long and 100mm in diameter. Find the discharge and the theoretical power required to run the pump. If the actual discharge is 4.2 lit/sec, find % of slip
This problem is similar to Example No : 22 and Page No: 4.124.
Ans:
(i) Qth = 0.004417 m/s
(ii) Pth =1.0833 kw
(iii) % of slip = 4.92%
Problem: 26
In a single acting reciprocating pump the bore and stroke are 100mm and 150mm respectively. The static head requirements are 4m suction and 18 m delivery. If the pressure at the end of delivery is atmospheric, calculate operating speed. The diameter of the delivery is 75 mm and the length of the delivery pipe is 24m. Determine the acceleration head at θ =33° from the start of delivery.
This problem is similar to Example No: 26 and Page No: 4.128.
Ans:
Acceleration head had = 6.45 m of water
Problem: 27
A single acting reciprocating pump has a diameter piston of 150mm and stroke length 350mm. The centre of the pump is 3.5 m above the water surface in the sump and 22m below the delivers water level. Both suction and delivery pipe have same diameter of 100mm and are 5m and 30m long respectively. If the pump is working at 30 rpm. Determine the pressure heads on the piston at the beginning middle and end of both suction and delivery strokes.
This problem is same as Example No: 30 and Page No: 4.136.
Problem: 28
A single cylinder double acting reciprocating pump has a piston diameter of 300 mm and stroke length of 400mm. When the pump runs at 45 rpm. It discharged 0.039 m3/s. Under a total head of 15m. What will be the volumetric efficiency, workdone per second and power required if the mechanical efficiency of the pump is 75%
This problem is same as Example No: 32 and Page No: 4.139.
Ans:
(i) ηv = 91.96%
(ii) P = 8.3188 kw
(iii) W/sec = 6.2391 × 103 w
Problem: 29
For single acting reciprocating pump piston diameter is 150mm, stroke length is 300mm, rotational speed is 50 rpm. The pump is required to lift water to a height of 18m. Determine the theoretical discharge, if the actual discharge is 4.0 lit/sec and mechanical efficiency is 80 %. Determine Volumetric efficiency, slip, theoretical power and actual power required.
This problem is similar to Example No: 31 and Page No: 4.138.
Ans:
(i) Qth = 4.4175 × 10-3 m3/sec
(ii) Slip = 4.175 × 10-4m2 sec
(iii) ηv = 90.54%
(iv) Power (P) = 975.0526 kw.
Problem: 30
Calculate the rate of flow in and out of the air vessel on the delivery side in a single acting reciprocating pump of 220mm bore and 330mm stroke running at 50 rpm. Also find the angle of crank rotation at which there is no flow in to out of the air vessel.
Given Data:
Piston diameter (D) = 220 = 0.22m
Stroke length L = 330 = 0.33m
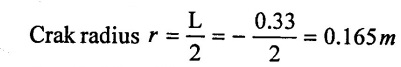
Speed (N) = 50 rpm
To find:
1) Rate of flow in and out of air vessel
2) Angle of crank rotation there is no flow
Solution:
Result:
(i) The water flowing into the air vessels (All crank rotation positions)
(ii) Crank angle no flow from of into air vessel (θ) = 18.56°
No comments:
Post a Comment