Problem - 1
An oil film of thickness 10 mm is used for lubrication between the two square parallel plates of size 0.9mx 0.9m each, in which the upper plate moves at 2 m/s required a force of 100 N to maintain this speed. Determine (i) Dynamic viscosity of the oil (ii) Kinematic viscosity of oil, if the specific gravity of the oil is 0.95.
Given data:
Oil film thickness (y) = 10mm = 0.01m
Size of plate = 0.9m × 0.9m
Velocity of moving plate (μ) = 2m/s
Specific gravity of oil (S) = 0.95
Required force on moving plate (F) = 100 N
To find:
(i) Dynamic viscosity of oil (μ)
(ii) Kinematic viscosity of oil (v)
Solution:

Result
(i) Dynamic viscosity (μ) = 0.61725N-s/m2
(ii) Kinematic viscosity (v) = 6.497 × 10-4 m2 / s
Problem - 2
If the velocity distribution over a plate is given by u = (2/3)y - y2 in which u is the velocity in m/s at a distance y meter above the plate, determine the shear stress at y = 0 and y = 0.15 m. The dynamic viscosity of fluid is 8.63 poise.
Given data:
Velocity distribution (u) = (2/3) y - y2 Dynamic viscosity (μ) = 8.63 poises
To find:
Shear stress (τ) at y = 0 & y = 0.15 m
Solution

Result
(i) Shear stress (τ) at y = 0 = 0.575N/m2
(ii) Shear stress (τ) at y = 0.15 = 0.316N/m2
Problem - 3
The space between two square parallel plates is filled with oil. Each sides of the plate in 75 cm. The thickness of the oil film is 10 mm. The upper plate which moves at 3 m/s, requires a force of 100 N to maintain the speed. Determine (i) Dynamic viscosity of oil (ii) Kinematic viscosity of the oil, if the specific gravity of oil is 0.9.
This problem is similar to Example No: 9 and page No: 1.18.
Ans:
(i) Dynamic Viscosity (μ) = 0.5925 N−s/m2
(ii) Kinematic Viscosity (v) = 6.584 × 104 m2 / s
[Note: Square Plate A = S2 = 0.75 × 0.75 0.5625 m2
Problem - 4
The velocity distribution over a plate is given by u = (3/4) y-y2. Where u is velocity in m/s and at a depth y in m above the plate. Determine the shear stress at a distance of 0.3 m from the top of plate. Assume dynamic viscosity of the fluid as 0.95 N-s/m2.
This problem is similar to Example No: 15 and page No: 1.25.
Ans: Shear stress (t) = 0.1425N/m2
Problem-5
A 200 mm diameter shaft slides though a sleeve 200.5 mm in diameter and 400 mm long, at a velocity of 30 cm/s. The viscosity of oil filling the angular space in μ = μ 0.1125N-s/m2. Find resistance to the motion.
Given data:
Sleeve diameter (D) = 200.5mm = 0.2005m
Shaft diameter (d) = 200mm = 0.2m
Sleeve length (L) = 400mm = 0.4m
Velocity (u) = 30 cm/s = -0.3 m/s
Dynamic viscosity (μ) = 0.1125 N-s/m2
To find:
Resistance to the motion (or) Force (F)
Solution:

Result:
Force (or) Resistance of the motion (F) = 33.75 N
Problem - 6
A fluid of specific gravity 0.9 flows along a surface with a velocity profile given by u = 4y-8y3 m/s. Where y is in m. What is the velocity gradient at the boundary? If the kinematic viscosity is 0.36m2/s, what is the shear stress at the boundary?
This problem is similar to Example No: 17 and page No: 1.27.
Ans:
(i) Velocity gradient (du/dy) = 4s-1
(ii) Shear stress (τ) = 1296N/m2
Problem - 7
A 0.5 m shaft rotates in a sleeve under lubrication with viscosity 5 poise at 200 rpm. Calculate the power lost for a length of 100 mm. The thickness of the oil is 1 mm.
This problem is similar to Example No: 12 and page No: 1.22.
Ans:
Power (P) = 2151.71 W
Problem - 8
Lateral stability of a long shaft 150 mm in diameter is obtained by means of a 250 mm. Stationary bearing having an internal diameter of 150.25 mm. If the space between bearing and shaft is filled with lubricant having a viscosity 0.245N-s/m2. What power will be required to overcome the viscous resistance when the shaft is rotated at constant rate of 180 rpm?
Given data:
Diameter of the shaft (d) = 150mm = 0.15m
Diameter of bearing (D) = 150.25 mm = 0.15025 m
Length of shaft (L) = 250mm = 250mm = 0.25 m
Viscosity (μ) = 0.245 N-s/m2
Speed (N) = 180rpm
To find:
Power required to overcome the resistance
Solution:
 Result:
Result:
Power lost due to viscosity resistance (P) = 461.48 watts
Problem - 9
The space between two square flat parallel plate is filled with oil. Each side of the plate is 600 mm. The thickness of the oil film is 12.5 mm. The upper plate, which moves at:2.5 m/s requires a force of 98 N, to maintain the speed. Determine
(i) Dynamic viscosity of the oil in poise
(ii) Kinematic viscosity of the oil in stokes. If the specific gravity of the oil is 0.95.
This problem is similar to Example No: 9 and page No: 1.18.
Result:
(i) Dynamic viscosity (μ) = 1.3635N-s/m2 (or) 13.635 poise
(ii) Kinematic viscosity (v) 1.434 × 10−3 m2 / s
= 14.34 stokes (1m2/s = 104 stokes)
Problem - 10
A 15 cm diameter vertical cylinder rotates concentrically inside another cylinder or diameter 15.10 cm. Both cylinders are 25 cm high. The space between the cylinders is filled with a liquid whose viscosity is unknown. If a torque of 12.0 N-m is required to rotate the inner cylinder at 100 rpm, determine the viscosity of the fluid.
Given data:
Diameter of inside cylinder (d) = 15cm = 0.15m
Diameter of outer cylinder (D) = 15.1cm = 0.151m
Height (or) Length of both cylinder (L) = 25cm = 0.25 m
Torque (T) = 12N - m
Speed (N) = 100rpm
To find:
Viscosity of fluid (μ)
Solution:
 Result:
Result:
Dynamic viscosity (μ) = 0.865 N − s / m2
Problem - 11
The velocity distribution over a plate is given by u = 2y2 – y2, where u is the velocity in m/s at a distance of y metre above the plate. Determine the velocity gradient and shear stress at the boundary and 1.5 m from it. Dynamic viscosity of the fluid is 0.9N-s/m2.
This problem is similar to AU solved problem No-2 and page No: 1.150.
Result:

Problem-12
The space between two parallel plates 5 mm apart, is filled with crude oil of specific gravity 0.9. A force of 2 N is required to drag the upper plate at a constant velocity of 0.8 m/s. The lower plate is stationary. The area of the upper plate is 0.09m2. Determine (i) dynamic viscosity in poise (ii) kinematic viscosity of oil in stokes.
This problem is similar to Example No-9 and page No: 1.18.
Result:
(i) Dynamic viscosity (μ) = 1.39 poise
(ii) Kinematic viscosity (v)=1.54 stokes
Problem - 13
Two large plane surfaces are 125 mm apart. The space between the surfaces is filled with oil of viscosity 0.972N-s/m2. A thin plate of 0.5 m2 area moves through the oil at velocity of 0.3 m/s. Calculate the drag force.
(i) When the thin plate is in the middle of the two plane surface.
(ii) When the thin plate is at a distance of 30 mm from any one of the planes.
This problem is similar to example No-22 and page No: 1.35.
Result:
(i) Drag force when plate is a placed at the middle of two surfaces (F) = 4.666N
(ii) Drag force when plate is placd at a distance of 30mm from one of the plane surface (F) = 6.395N
Problem - 14
The dynamic viscosity of an oil used for lubrication between a shaft and sleeve is 6 poise. The shaft diameter is 0.4 m and rotates at 190 rpm. Calculate power lost in the bearing for a sleeve length of 90 mm. The thickness of oil film is 1.5 mm.
This problem is similar to solved Example No-12 and page No: 1.22.
Answer:
Power lost (P) = 11.941 watts
Problem - 15
A 400 mm diameter shaft is rotating at 200 rpm in bearing of length 120 mm. If the thickness of oil film is 1.5 mm and the dynamic viscosity of the oil is 0.7N-s/m2. Determine (i) Torque require to overcome friction in bearing (ii) Power utilized in overcoming viscous resistance. Assume a linear velocity profile.
This problem is similar to solved Example No – 12 and page No: 1.22.
Answer:
Torque (T) = 35.97 N – m
Power (P) = 715.686 watts
Problem - 16
The velocity profile of fluid over a plate is parabolic with its vertex 200 mm from the plate, where the velocity is 1.2 m/s. calculate the velocity gradients and shear stresses at 50 mm and 200 mm from the plate, if the viscosity of the fluid is 0.8N-s/m2.
This problem is similar to Example No - 18 and page No: 1.28.
Answer:

Problem-17
A plate 1m2 in area and weight 150 N slides in an inclined plane of angle θ = sin-1(5/13) with horizontal with a velocity of 5 cm/s. If the thickness of oil film over the plane is 1.5 mm, estimate the viscosity of oil.
Given data:
Area of the plate (A) = 1m2
Weight of the plate (W) = 150N
Inclined plane angle (θ) = sin-1 (5/13) = 22.62°
Velocity of the plate (u) = 5cm/s = 0.05m/s
Oil film thickness (y) = 1.5 × 10-3 m
To find:
Viscosity of oil (μ)
Solution:
 Result:
Result:
Dynamic viscosity (μ) = 1.731N-s/m2
Problem - 18
The dynamic viscosity of an oil used for lubrication between a shaft and sleeve is 10 poise. The shaft rotates at 200 rpm. The power lost in the bearing for a sleeve length of 100 mm is 250 watts. The thickness of oil film is 1.5 mm. Calculate the diameter of the shaft and sleeve.
Given data:
Viscosity of oil (μ) = 10 poise = 1N-s/m2
Speed (N) = 200 rpm
Length of sleeve (L) = 100mm = 0.1m
Power (P) = 250 watts
Thickness of oil film (y) = 1.5mm = 1.5 × 10-3 m
To find:
(i) Diameter of the shaft
(ii) Diameter of the sleeve
Solution:

Result:
(i) Diameter of the shaft (d) = 0.2216m
(ii) Diameter of sleeve (D) = 0.2246m
Problem-19
When a pressure of 20.7 MN/m2 is applied to 100 lits of a liquid its volume decreases by one litre. Find the bulk modulus of the liquid and identify this liquid.
Given data:
Pressure (P) = 20.7MN/m2 = 20.7 × 106 N/m2
Initial volume (U1) = 100lits = 0.1m3
Change in volume (dU) = 1 litre = 0.001m3
To find:
Bulk modulus of the liquid
Solution:
 Result:
Result:
Bulk modulus (K) = 207 × 103 N/m2
Problem - 20
Assuming the Bulk modulus of elasticity of water is 2.07 × 106 KN/m2 at standard atmospheric condition, determine the increase of pressure necessary to produce one percent reduction in the volume at the same temperature.
Given data:
Bulk modulus (K) = 2.07 × 106 KN/m2 = 2.07× 109 N/m2
Volumetric strain (dU/U) = 1% = 0.01
To find:
Increase in pressure (or) change in pressure
Solution:

Result:
Change in pressure (dP) = 2.07 × 107 N/m2
Problem - 21
A liquid is compressed in a cylinder having a volume of 0.012 m3 at a pressure of 690 N/m2. What should be the new pressure in order to make its volume 0.0119 m3? Assume Bulk moduls of elasticity (K) for the liquid is 6.7 × 101 N/cm2.
Given data:
Initial volume (U1) = 0.012m3
Initial pressure (P1) = 690 N/cm2 = 690 × 101N/m2
Final volume (U2) = 0.0119m3
Bulk modulus (K) = 6.9 × 104 N / cm2 ⇒ (K) = 6.9 × 108 N/m2
To find:
Final pressure (P2)
Solution:
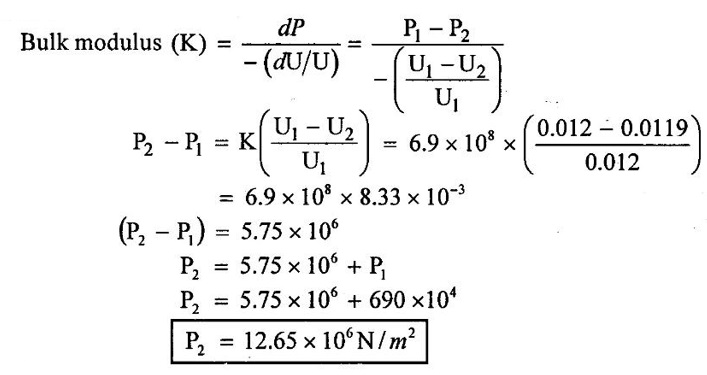
Result:
Final pressure (P2) = 12.65 × 106N/m2
Problem - 22
Find the height through which water rises by capillary action in a 2 mm bore, if surface tension at the prevailing temperature is 0.075 g/cm.
This problem is similar to Example No: 37 and Page No: 1.57.
Ans:
Capillary rise (h) = 15mm
Problem - 23
Calculate the capillary rise in glass tube of 3 mm diameter when immersed in mercury. Take the surface tension and angle of contact of mercury as 0.52 N/m and 130° respectively. Also determine the minimum size of the glass tube, if it is immerses in water, given that the surface tension of water is 0.0725 N/m and capillary rise in the tube is not to exceed 0.5 mm.
Given data:
For mercury
Diameter of glass tube (d) = 3mm = 0.003 m
Surface tension (σ)mercury = 0.52 N/m
Angle of contact (β) = 130°
For water
Surface tension (σwater) = 0.0725N/m
Capillary rise hwater = 0.5mm = 0.5 x 10-3 m
To find:
(i) Capillary rise for mercury
(ii) Minimum size of glass tube for water
Solution:

Result
(i) Capillary rise of mercury (h) = -3.34 mm
(ii) Diameter of glass tube for water (d) = 59.1mm
Problem - 24
Calculate the capillary effect in a glass tube 5 mm diameter, when immersed in (i) water (ii) mercury. The surface tension of water and mercury in contact with air are 0.0725 N/m and 0.57 N/m respectively. The angle of contact of mercury is 130°.
This problem is similar to Example No: 37 and Page No: 1.57.
Ans:
(i) Capillary depression for mercury (h) = −1.965mm
(ii) Capillary rise for water (h) = 5.91mm
Problem - 25
Calculate the capillary effect in millimeter in a glass tube of 4 mm diameter. When immersed in (i) water and (ii) mercury. The temperature of the liquid is 20°C and values of surface tension of water and mercury at 20°C in contact with air are 0.0735 N/m and 0.57 N/m respectively. The contact angle for water 0 = 0 and for mercury θ = 130°. Take specific weight of water at 20°C as equal to 9790 N/m3 and specific gravity of mercury is 13.6.
Given data:
Glass tube of diameter (d) = 4mm = 0.004 m
Surface tension (σmercury) = 0.57N/m
Surface tension (σwater) = 0.0735 N/m
Angle of contact for water (β) = 0
Angle of contact for mercury (β) = 130°
Specific weight of water (w) = 9790 N/m3
Specific gravity of mercury (s) = 13.6
To find:
(i) Capillary rise for mercury
(ii) Capillary rise for water
Solution:
 Result:
Result:
(i) Capillary rise for mercury (h) = -2.46 mm
(ii) Capillary rise for water (h) = 7.56mm
Problem - 26
A capillary tube having inside diameter 6 mm is dipped in CCl4, at 20°C. Find the rise of CCl4, in the tube, if surface tension is 2.67 N/m and specific gravity is 1.594 and contact angle 0 is 60o and specific weight of water at 20°C is 9981N/m3.
This problem is same as Example No-46 and page No: 1.63.
Ans:
h = 55.94mm (or) 0.0594 m
Problem - 27
AU-tube is made of two capillary of diameter 1.0 mm and 1.5 mm respectively. The tube is kept vertically and partially filled with water of surface tension (σ) 0.0736 N/m and zero contact angle. Calculate the difference in the levels of the menisci causes by the capillary.
This problem is similar to Example No - 39 and page No: 1.59.
Ans:
Difference in menisci level x = 0.01 m
Problem - 28
A 1.9 mm diameter tube is inserted into an unknown liquid whose density in 960Kg/m3, and it is observed that the liquid rises 5 mm in the tube, making a contact angle of 15°. Determine the surface tension of the liquid.
Given data:
Diameter of glass tube (d) = 1.9mm = 0.0019m
Contact angle (B) = 15°
Capillary rise (h) = 5mm = 0.005 m
Density (p) = 960 Kg/m3
To find:
Surface Tension of liquid
Solution:
 Result:
Result:
Surface Tension (0) = 0.0231N/m
Problem - 29
What do you mean by surface tension? If the pressure difference between the inside and outside of the air bubble of diameter, 0.01 mm is 29.2 kpa, what will be the surface tension at air water interface? Derive an expression for the surface tension in the air bubble and from it, deduce the result for the given conditions.
This problem is similar to Example No: 43 and refer page No: 1.51 for derivation.
Ans:
σ = 0.0365 N/m
Problem - 30
AU-tube is made up of two capillaries of bore 5 mm and 10 mm respectively. The tube is held vertically and is partially filled with a liquid of surface tension 0.051 N/m and zero contact angle. Calculate the mass density of the liquid if the estimated difference in the level of two mansisci is 12.5 mm.
Given data:
Diameter of tubes d1 = 5mm = 5 × 10-3
d2 = 10mm 10 × 10-3
Surface tension (σ) = 0.057 N/m
Contact angle (β) = 0
Difference level (h1 – h2) = 10.5mm = 0.0125m
To find:
Mass density of the liquid
Solution:
 Result:
Result:
Mass density (ρ) = 166.36Kg/m3
Problem - 31
At a depth of 8 km in an ocean, the pressure is 82MN/m2. Assume the specific weight of surface as 1025 Kg/m3 and the average Bulk modulus of elasticity as k = 2350 Mpa, for that pressure range
(i) What will be the change in specific volumes between that of the surface and at that depth
(ii) What will be the specific volume at that depth
(iii) What will be the specific weight at that depth
Given data:
Pressure (P) = 82MN/m2 = 82 × 106 N/m2
Specific weight (w) = 1025Kg/m3
Bulk modulus (K) = 2350 mpa = 2350 × 106 N/m2
Depth of ocean (h) = 8 Km = 8000 m
To find:
(i) Change of specific volume (dv),
(ii) Specific volume at 8 Km depth
(iii) Specific weight at 8 Km depth
Solution:

Result:
(i) Change of specific volume = 3.404 × 10-5 m3/Kg
(ii) Specific volume at 8 Km depth = 9.416 × 10-4 m3 /Kg
(iii) Specific weight at 8 Km depth = 10418.9N/m3
Problem - 32
The maximum blood pressure in the upper arm of a healthy person is about 120 mm of Hg. If a vertical tube open to the atmosphere is connected to the vein in the arm of the person, determine how high the blood will rise in the tube. Take the density of the blood to be 1050 Kg/m3.
Given data:
Head of mercury (x) = 120 mm = 0.12 m
Density of blood (ρb) = 1050 Kg/m3
To find:
Height of blood will rise in the tube, (H)
Solution:
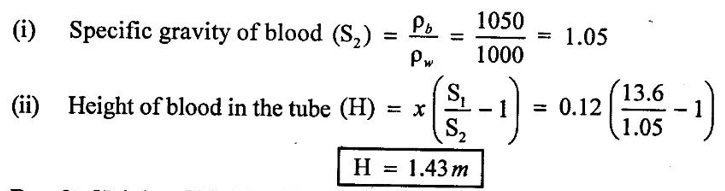
Result:
Height of blood will rise in the tube H = 1.43 m
Problem - 33
A pipe line 60 cm in diameter bifurcates at a Y – Junction into two branches 40 cm and 30 cm in diameter. If the rate of flow in the main pipe is 1.5, and the mean velocity of flow in the pipe is 7.5 m/s, determine the rate of flow in the 40 cm pipe.
Given data:
Main pipe diameter (D) = 60 cm = 0.6m
Branch pipe diameter at (1) d1 = 40cm = 0.4m
Branch pipe diameter at (2) d2 = 30cm = 0.3m
Rate of flow in main pipe (Q) = 1.5 m3/sec
Velocity at pipe (V2) = 7.5m/s
To find:
Rate of flow in pipe (1) (Q1)
Solution:
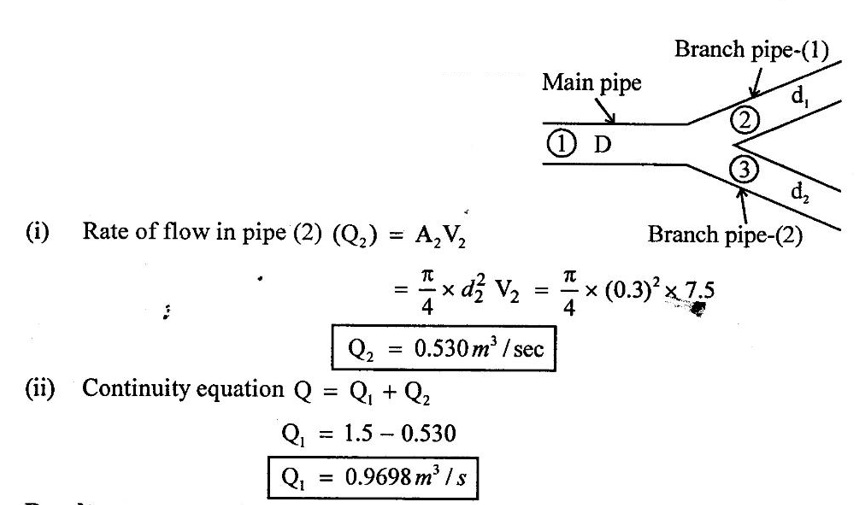
Result:
Rate of flow in pipe (Q1) = 0.9698 m3 / sec
Problem - 34
The drainage pipe is tapered in a section running with full of water. The pipe diameters at the inlet and exit are 1000 mm and 500 mm respectively. The water surface is 2m above the center of the inlet and exit is 3 m above the free surface of the water. The pressure at the exit is 250 mm of Hg vaccum. The friction loss between the inlet and exit of the pipe is 1 /10 of the velocity head at the exit. Determine the discharge through the pipe.
Given data:
Inlet pipe diameter (D1) = 1000mm = 1m
Outlet pipe diameter (D2) = 500 mm = 0.5 m
Datum head at inlet (z1) = 0m
Datum head at outlet (z2) = 5m
Inlet pressure head (P1/w) = 2m of water
Outlet pressure head (P2/w) = 250mm of Hg vaccum
Loss of head (h2) = 1/10 × v22/2g
To find:
Discharge through the pipe (Q)
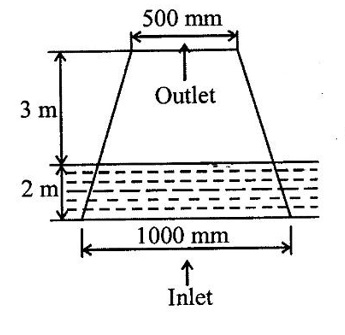
Solution:
 Result:
Result:
Rate of flow (Q) = 0.57m3/s
Problem-35
A pipe containing water at 180 KN/m2 pressure is connected by a differential gauge to another pipe 1.6 m lower than the first pipe and containing water at high pressure. If the difference in heights of 2 mercury columns of the gauge is equal to 90 mm, what is the pressure in the lower pipe?
Given data:
Upper pipe pressure (P1) = 180 KN/m2
Difference in datum head (z1 - z2) = 1.6m
Manometer readingss (x) = 90mm = 0.09 m
To find:
Lower pipe pressure (P2)
Solution:

Result:
Lower pipe pressure (P2) = 184.57 KN/m2
Problem - 36
The converging pipe with inlet and outlet diameters of 200 mm and 150 mm carries the oil whose specific gravity is 0.8. The velocity of oil at the entry in 2.5 m/s. Find the velocity at the exit of the pipe and oil flow rate in Kg/sec.
Given data:
Inlet pipe diameter (d1) = 200mm = 0.2m
Outlet pipe diameter (d2) = 150mm = 0.15m
Specific gravity of oil (S) = 0.8
Inlet velocity (V1) = 2.5m/s
To find:
(i) Velocity of exit pipe (V2)
(ii) Rate of flow of oil (Q)
Solution:

(iii) Rate of flow (Q) = A1V1
= 0.0314 × 2.5
= 0.0785 m3/s
(iv) Velocity of exit pipe (V2) = Q/A2

Result:
(i) Velocity of exit pipe (V2) = 4.44 m/s
(ii) Rate of flow (Q) = 0.0785 m3/s
Problem - 37
A 15 cm diameter vertical pipe is connected to 10 cm diameter vertical pipe with a reducing socket. The pipe carries water at the flow rate of 100 lit/sec. At point 2 in the 10 cm pipe located 1.0 m below point 1, the gauge pressure is 175 kpa.
(i) Find whether flow is upward /downward
(ii) Head loss between two points
Given data:
Pipe diameter at point (1) (d1) = 15cm = 0.15m
Pipe diameter at point (2) (d2) = 10cm = 0.10m
Rate of flow (Q) = 100 lit/sec = 0.1m3/sec
Pressure at point (1) (P1) = 250 kpa = 250 × 103N/m2
Pressure at point (2) (P2) = 175 kpa = 175 × 103 N/m2
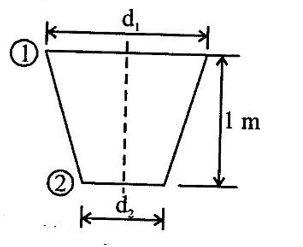
To find:
(i) Direction of flow
(ii) Head loss between two ports
Solution:
Result:
(i) Flow in downwards point (1) to point (2)
(ii) Loss of head (h) = 2.01 m
Problem - 38
The water is flowing through a taper pipe of length 100 mm having diameters 600 mm at the upper end and 300 mm at the lower end, at the rate of 50 lit/sec. The pipe has a slope of 1:30. Find the pressure at the lower end of the pressure at the height level is 19.62N/cm2.
This problem is similar to Example No-56 and page No-1.99.
Answer:
Pressure at lower end (P2) = 226.375 × 103 N / m2
Problem-39
An orifice meter with orifice diameter 15 cm is inserted in a pipe of 30 cm diameter. The pressure of the upstream and downstream of orifice meter is 14.7N/cm2 and 9.81N/cm2. Find discharge, if Cd = 0.6.
This problem is similar to Example No - 82 and page No 1.133.
Ans:
Discharge (Q) = 0.1083 m3/s
Problem - 40
A horizontal venturimeter with inlet diameter 200 mm and throat diameter 100 mm is employed to measure the flow of water. The reading of the differential manometer connected, to the inlet is 180 mm of mercury. If C4 = 0.98, determine the rate of flow.
This problem is similar to Example No – 71 and page No 1.119.
Ans:
Rate of flow (Q) = 0.053m3 / s
Problem - 41
A 300 × 150 venturimeter is provided in a vertical pipe line carrying oil of relative density 0.9 flow being upwards. The differential U-tube mercury manometer show a gauge deflection of 25 mm. Calculate the discharge of oil, if the co-efficient of meter is 0.98.
This problem is similar to Example No-76 and page No 1.125.
Ans:
Rate of flow (Q) = 0.1488 m3/s
Problem - 42
A pipe of 300 mm diameter inclined at 30o to the horizontal is carrying gasoline (Specific gravity = 0.82). A venturimeter is fitted in the pipe to find out the flow rate whose throat diameter is 150 mm. The throat is 10 m from the entrance along its length. The pressure gauges fitted to the venturimeter read 140KN/m2 and 80 KN/m2 respectively. Find out the co-efficient of discharge of venturimeter if the flow is 0.2m3/s.
Given data:
Inclined plane (θ) = 30°
Pipe diameter (d1) = 300cm = 0.3m
Throat diameter (d2) = 150mm = 0.15m
Specific gravity (S) = 0.82
Pressure (P1) = 140 KN/m2 = 140 × 103 N/m2
Pressure (P2) = 80KN/m2 = 80 × 103 N/m2
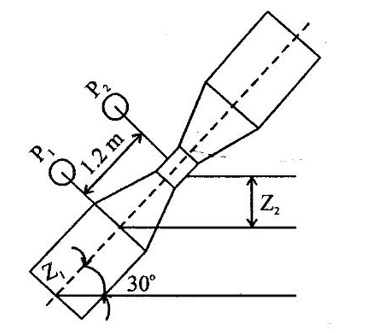
To find:
Co-efficient of discharge of venturimeter (Cd)
Solution:

Result:
Coefficient of discharge Cd = 0.905
Problem - 43
A pipe line 175 mm diameter branches into two pipes which delivers water at atmospheric pressure. The diameter of the branch - I which is at 35° counter clock wise to the pipe axis is 75 mm and the velocity at outlet is 15 m/s. The branch – II is at the pipe center line in the clock wise direction has a diameter 100mm and the outlet velocity is 15 m/s. The pipe line in a horizontal plane. Determine the magnitude and direction of the forces on the pipes.
Given data:
Diameter of main pipe (d) = 175mm = 0.175m
Diameter of branch pipe (d1) = 75mm = 0.075m
Diameter of branch pipe (d2) = 100mm = 0.1m
Velocity of branch pipe-1 (V1) = 15m/s
Velocity of branch pipe-2 (V2) = 15m/s
To find:
Magnitude and direction of the force on the pipes
Solution:
 Result:
Result:
Force in x direction (Fx) = 3931.96 N
Force in y direction. (Fy) = 112.720 N
Direction of resultant force (θ) = 1.642° C
Problem - 44
Find the discharge of water flowing through a pipe 30 cm diameter placed in out inclined position where a venturimeter is inserted having a throat diameter of 15 cm. The difference of pressure between the main and throat is measured by a liquid of specific gravity 0.6 in an inverted U-tube which gives a readings of 30 cm. The loss of head between the main and throat is 0.2 times the kinetic head of the pipe.
This problem is similar to Example No - 78 and page No 1.126.
Ans:
Discharge (Q) = 0.0278 m3/s
Problem - 45
A 0.3 m diameter pipe carrying oil at 1.5 m/s velocity suddenly expands to 0.6 m diameter pipe. Determine the discharge and velocity in 0.6 m diameter pipe.
This problem is similar to Example No - 47 and page No 1.87.
Ans:
Q2 = 0.1060 m3 / s, V2 = 0.3750m/s
Problem-46
According to Torricelli's theorem, the velocity of a fluid, draining from a hole in a tank is V = √2gh, where h is the depth of water above the hole let the hole have area (Ab) and the cylindrical tank have bottom area Ac. Derive the formula for the time to drain the tank from an initial depth (h1).
Given data:
Area of the hole = Ab
Área of cylindrical area = Ac
Velocity (V) = √2gh
Solution:
Integrating on both sides,
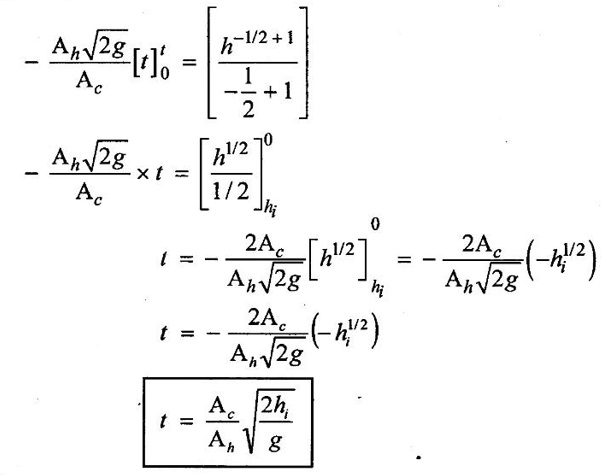
Result:
Time to drain the tank 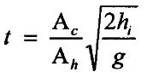
Problem - 47
Water enters the bottom of the cone as shown in figure, at a uniformly average velocity V = Lt. If d is very small, derive an analytic formula for the water surface rise h(t), assuming h=0 at t=0.
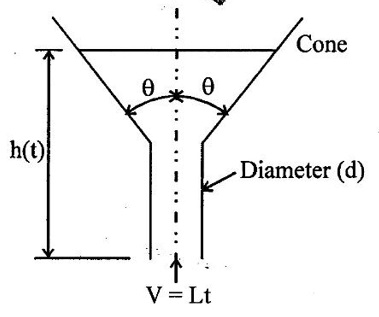
Given data:
Average velocity (V) = Lt, h = 0 at t = 0
Solution:

By using the mass, volume, and density relationship
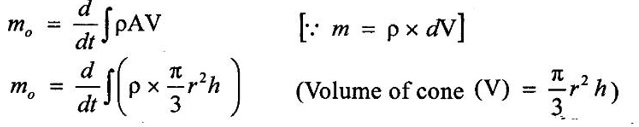
But the cross section of the cone is two iso-right angle triangles. So the radius of cone can be written as, r = h tan θ
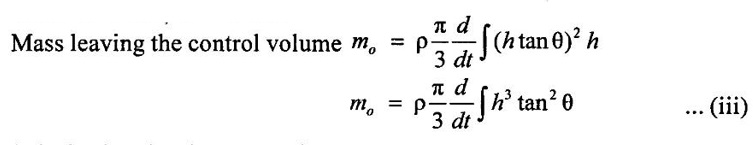
Substituting the above equation (ii) and (iii) in equation (i)
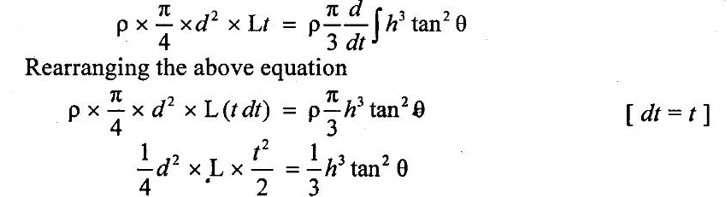
Since, the integration of constant on right hand side remains the same. Therefore, the analytical formula for water surface rise in terms of h(t) is given by
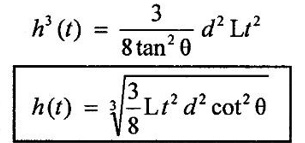
Result:
Water surface rise 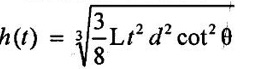
Problem - 48
A 300 mm irrotation × 150 mm venturimeter is provided in a vertical pipeline varying of all relative density 0.9, the flow being upwards and the elevation of 30 cm. The differential U-tube mercury manometer shows a gauge deflection of 25 cm. Calculate the discharge of oil and pressure difference between entrance and throat section, if the co-efficient of discharge is 0.98.
Given data:
Diameter at inlet (d1) = 300mm = 0.3m
Diameter at throat (d2) = 150mm = 0.15m
Manometer gauge deflection (x) = 52cm = 0.25m
Flow in upwards, so (z2 − z1) = 30cm = 0.3m
To find
(i) Discharge (Q)
(ii) Pressure difference between two sections (P1 - P2)
Solution:
 Result:
Result:
Discharge (Q) = 148.85 lit/sec
(ii) Pressure difference (P1 - P2) = 33.788 KN/m2
No comments:
Post a Comment