1. Introduction
When a fluid flowing through a pipe certain resistance is offered to the flowing fluid, it results in causing a loss of some energy (head) is called losses in pipes.
When fluid flows through a pipe line, it encounter resistance due to viscosity of the fluid, the roughness existing in the interior surface of the pipe line and resistance offered by various pipes fittings. Turbulence is produced in fluid flow due to resistance causing loss of energy and pressure head.
2. Different types of Loss of Head in Fluid Flow Through Pipe Line
The loss of head in pipe line can be constant velocity head loss and variable velocity head loss due to changing the cross section. The constant velocity heat loss takes place due to
(i) Friction in the pipe line
(ii) Kinetic energy loss.
The head loss due to friction results due to
(i) Resistance offered by the roughness of the pipe surface when fluid flow through pipe surface.
(ii) Resistance offered by the fluid layers to each other.
Incase the length of a pipe line is more than 500 times to its diameter, Then pipe line is termed as long pipe line and such pipeline has head loss due to friction is called as major loss.
When the fluid flows out of the pipe line at the exit, it has certain velocity. Which is head loss due to kinetic energy fluid out is called as a minor loss.
Variable velocity head loss takes place due to variable velocity resulting in a pipe line whenever there is a change of cross section inside the pipe line. For example. There are changes in cross section due to
(i) Pipe entrance from the reservoirs.
(ii) Sudden enlargement
(iii) Sudden contraction
(iv) Many pipe fittings etc.
3. Major Energy (Head) Losses in Pipes
Major loss of energy occurred in constant velocity head due to friction when fluid flow through the pipe surface.
These losses can be calculated by
(i) Darcy - weisbatch formula
(ii) Chezy's formula
1. Darcy – weisbatch formula
When the flow is transient (or) turbulent we cannot use Hagen-poiseuill's equation to find loss of head due to friction. So when pipe flow is turbulent there we can use Darcy's formula to find the loss of head (hf) due to friction.
Darcy's weisbatch equation

Where,
hf = Loss of head due to friction in m
f = co-efficient of friction (no unit)
f = 16 / Re for laminar flow (Re < 2000)
f = 0.0791/ (Re)0.25 for Reynolds number varying from 4000 to 106
L = length of the pipe in m.
V = mean velocity (or) Average velocity in m/s
d = diameter of the pipe in m.
2. Chezy's Equation.
Consider uniform horizontal pipe having steady flow and control volume enclosed between two sections 1 and 2 of the pipe shown in figure 2.23.

Let
P1 = pressure intensity of section 1 - 1
V1 = velocity of flow at section 1 - 1
P2, V2 are values of pressure intensity and velocity at section 2-2 respectively.
L = Length of pipe between sections 1 - 1 to 2-2
d = diameter of pipe
f' = frictional resistance per unit wetted area per unit velocity
hf = Loss of head due to friction.
Apply Bernoulli's Equation.
Total head at 1-1 = Total head 2-2 + Loss of head due to friction between 1 - 1 to 2 - 2

Z1 = Z2 as pipe in horizontal
V1 = V2 as pipe diameter is same
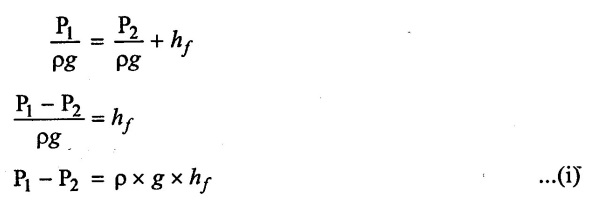
The forces acting on the fluid between sections 1- 1 to 2 - 2
(i) Pressure force at section 1 - 1 = pressure × Area of pipe
= P1 × A
(ii) Pressure force at section 2 - 2 = P2 × A
(iii) Frictional force (F) = frictional resistance per unit area per unit velocity × wetted area × velocity2
F = ƒ' × лd L × V2
= f' × P × L × V2 (⸫ Perimeter (P) = лd)
Resolving the forces acting in the horizontal direction
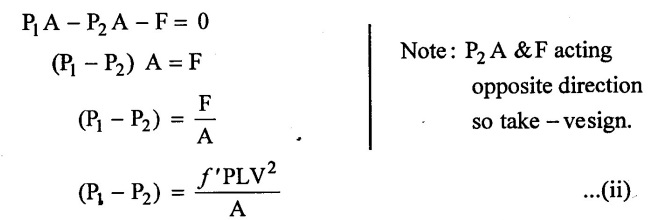
(P1 – P2) value from equation (i) Apply in equation (ii)

The ratio of area of pipe to perimeter (wetted) if the pipe is called Hydraulic mean depth (m)

The above equation is called Chezy's equation.
4. Minor Losses in Pipe Flow
The loss of energy due to change of velocity of the flowing fluid in magnitude (or) direction is called minor loss of energy. In case of long pipes, these losses are usually small as compared to the loss of energy due to friction and hence, they are called minor losses.
If L/d ≥ 1000 Minor losses may be neglected as they are relatively smaller in magnitude. But incase of short pipes, there losses are comparable with the loss of energy due to friction. This losses are disturbance in the flow pattern. Totally short pipe flow is to be consider minor losses where as long pipe it does not make any serious effect.
The minor loss of energy (head) includes the following cases.
(i) Loss of head due to sudden enlargement
(ii) Loss of head due to sudden contraction
(iii) Loss of head due to at entrance of the pipe
(iv) Loss of head at exit of a pipe
(v) Loss of head due to an obstruction in a pipe
(vi) Loss of head due to bend in the pipe
(vii) Loss of head in various pipe fittings.
1. Loss of head due to sudden enlargement
Consider a horizontal pipe line in which there is a sudden enlargement cross- section from A1 to A2 (A2 > A1). Take two sections 1 - 1 and 2 - 2 before and after the enlargement as shown in figure. 2.24
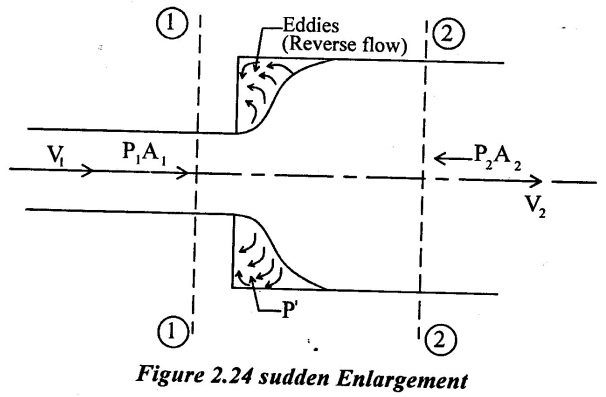
Where,
P1 = Pressure intensity at sections 1 - 1
V1 = Velocity of flow at section 1 - 1
A1 = Area of pipe at section 1 - 1
P2, V2 and A2 are corresponding values at section 2 - 2
Apply Bernoulli's equation

The loss of energy (head) in sudden enlargement (or) expansion is mainly due to turbulent eddies that are formed in the corner shown in figure. 2.24.
As area is suddenly increased from A1 to A2, fluid does not fill up the area (A2 -A1) initially, and this area is filled up by reversed flow initiated by eddies at a later stage. The pressure P is determined experimentally in area (A2 - A1) which is formed to be equal to initial inlet pressure P1
The resultant force acting on the fluid between section 1 - 1and 2 - 2 in the direction of flow is

The net force acting on the fluid is equal to the rate of change of momentum in the direction of flow as per Newton's second law of motion.

The equation (iii) will apply in equation (i)
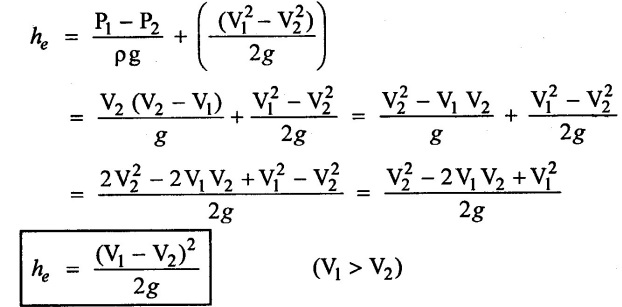
Which gives the loss of he due to sudden enlargement. This loss of energy (head) equation was first obtained by J.C Borda and L. Carnot and is therefore Known as Borda - Carnot equation of head loss.
2. Loss of head due to sudden contraction
Consider a liquid flowing in a pipe which has a sudden contraction in area A1 to A, as shown in figure 2.25. Consident two sections1-1 and 2-2 before and after the contraction. As the liquid flows from large pipe to small pipe the area of flow goes on decreasing and becomes minimum at a section C-C as shown in figure 2.25
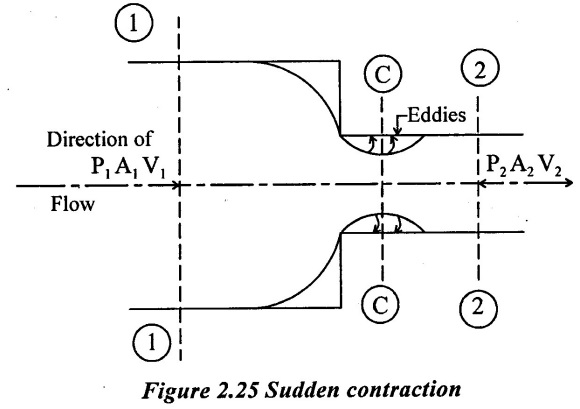
This section at which the area of flow is minimum is called Vena- contracta. [i.e., The minimum cross-sectional area of flow at which the area of flow changes from a contraction to expansion is called the Vena- contracta]
After section C-C, a sudden enlargement of the area takes place (section C-C to 2-2). The loss of head due to sudden contraction is actually due to sudden enlargement from Vena contracta to small pipe - Based on this assumption consider sections C-C to 2-2
Let, Ae - Area of flow at section C - C
Ve - Velocity of flow at section C - C
A2 -Area of flow at section 2 - 2
V2 - Velocity of flow at section 2 - 2
he - Loss of head due to sudden contraction
Loss of head due to sudden enlargement

Cc - co-efficient of contraction and it defined as the ratio of cross-sectional area at Vena contracta (Ac) to cross sectional area at section 2-2 (A2)
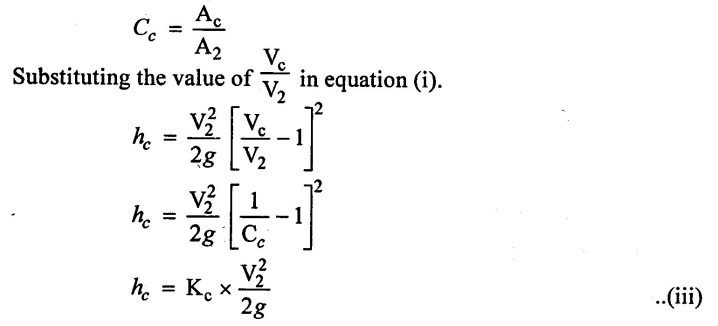
Kc - co-efficient of sudden contraction is function of diameters ratio (d2/d1)
If the value of Cc is assume 0.62 then,

If the value of Cc is not given then the head loss due to contraction is taken as
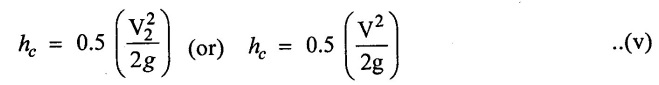
The co-efficient of sudden contraction Kc which is a function of the diameters ratio d2/d1. Its value is given in following Table. 2.2

3. Loss of head at the entrance of the pipe

When a liquid enters in a pipe from a large vessel e.g tank (or) reservoir, some loss of head or energy occurs at the entrance to pipe which is known as intet loss of energy or head. While the liquid enters the pipe, it gets contracted to a narrow neck and again expands to the entire cross-section of the pipe. The expression for loss of head at entrance 'h' will be similar to that the loss of head due to sudden contraction 'hc', starting the expression from equation

Such type of flow will give rise to a condition in which cross sectional area of tank A → ∞ and diameter ratio D/d tends to zero. Thus, from the table 2.26 loss co-efficients (Kc) corresponding to this condition is 0.5.
(i) h = 0 [Set well rounded entrance]
(ii) hi = 0.5 V2/2g [For sharp edged entrance]
(iii) hi = V2/2g [For re-entrant (or) protruding entrance
Commonly used sharp edged entrance so hi = 0.5 V2/2g
4. Loss of head at the exit of a pipe.
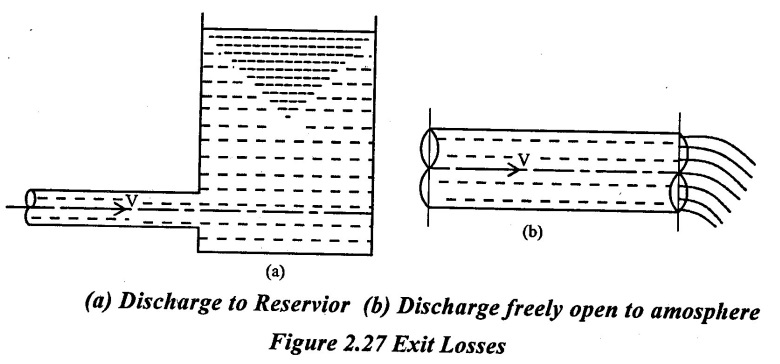
The outlet end of as pipe carrying a liquid may be either left free so that liquid is discharged freely or it may be connected to a large reservoir as shown in 2.27. In case of a reservoir, the pipe outlet becomes submerged and the liquid is discharged into a large body of static liquid. This case may be treated in the similar manner as that of loss of head due to sudden enlargement. The expression is
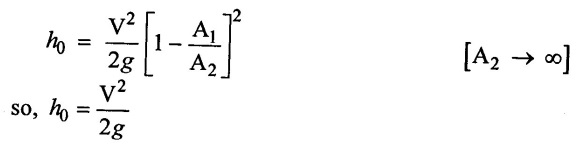
5. Loss of head due to an obstruction in pipe
Consider a pipe of cross-sectional area 'A' having an obstruction as shown in figure 2.28.
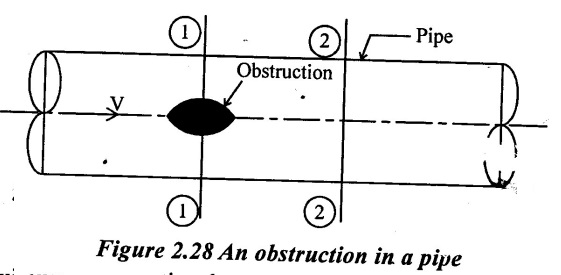
Let a = maximum cross sectional area of obstruction
V = velocity of liquid in pipe
(A - a) = cross sectional area of liquid at section 1 - 1
As the fluid flows and passes through section 1 1, a vena contracta is formed beyond section 1 - 1, after which the stream of liquid widens again and velocity of flow at section 2 - 2 becomes uniform and equal to velocity V in the pipe. This situation is similar to the flow of liquid through sudden enlargement.
Let Vc = velocity of liquid at vena - contracta then, loss of head due to obstruction is equal to the head due to enlargement from vena - contracta to section 2-2

Where
АC = cross, sectional area at vena-contra
If Cc = co-efficient

Substututing the value of Ac in equation (ii), we set

Substituting the value of Vc in equation (i),

6. Loss of head in pipe fitting.
The loss of head in the various pipe fittings, such as valves, elbows and bends etc, occurs because of their irregular interior surfaces which, produce large scale turbulence.
The loss of head or energy in various pipe fittings is expressed as
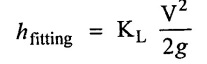
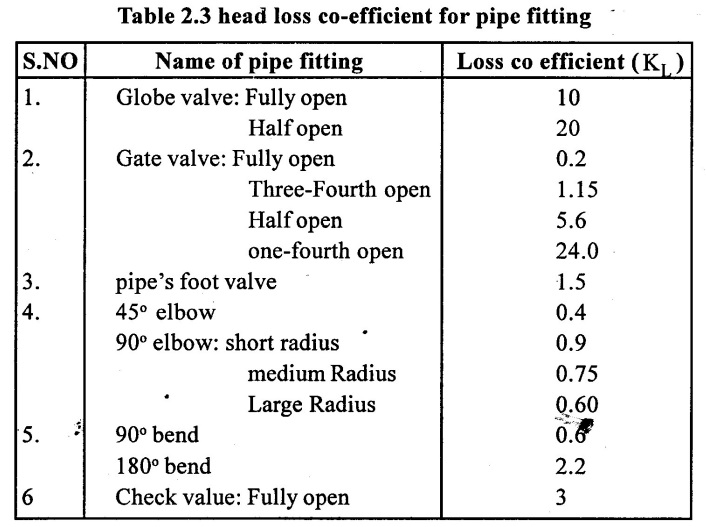
Where V is the mean velocity in the pipe and KL is the head loss co efficient is dependent on Reynolds number and the magnitude of which depends upon the shape of the fitting ((ie) angle of bend, radius of bend, opening of the value etc). The value of KL is found by experiment. The table 2.3 gives the values of KL for various common pipe fitting.
5. Solved Examples based on pipe losses
Example - 45
Find the head lost due to friction in a pipe of diameter 280mm and length 50m, through which water is flowing at a velocity of 3 m/s using (i) Darcy formula (ii) chezy's formula. Take C = 60 and v for water = 0.01 stroke.
Given data:
Diameter of pipe (d) = 280mm = 0.28m
Length (L) = 50m
velocity (v) = 3 m/s
Chezy's constant (c) = 60
Kinematic viscosity v = 0.01 stroke = 0.01 cm2/s
v = 0.01 × 10-4 m2/sec
To find:
Head Loss due to friction by using
(i) Darcy formula
(ii) Chezy's formula
Solution:

W.K.T

Result:
Loss of head due to friction by using
(i) Darcy formula hf = 0.8552m
(ii) Chezy's formula hf = 1.7857m
Example - 46
Find the diameter of a pipe of length 1700m when the rate of flow of water through the pipe is 200 lits/sec and the head lost due to friction is 4m. Take the value of C = 50 in Chezy's constant
Given data:
Length of pipe (L) = 1700m
Rate of flow (Q) = 200 lit/sec = 200 × 10-3 m3/s
Q = 0.2 m3/s
Heat loss due to friction (hf) = 4m
Chezy's constant (c) = 50
To find:
Diameter of pipe (d)
Solution:

W.K.T

Result:
Diameter of pipe (d) = 0.535m.
Example - 47
A crude oil of kinematic viscosity 0.45 stoke is flowing through a pipe of diameter 300mm at the rate of 300 lit/sec. Find the head lost due to friction for a length of the pipe.
Given Data:
Kinematic viscosity v = 0.45 stoke = 0.45 × 10-4 m2/sec
Diameter of pipe (d) = 300mm = 0.3m
Discharge (Q) = 300 lit/sec = 0.3 m3/s
Length of pipe (L) = 50m
To find:
Head lost due to friction (hf).
Solution:

Result:
Loss of head due to friction hf = 3.72 m.
Example - 48
An oil of specific gravity 0.8 is flowing through a pipe of diameter 300mm at rate 450 lit/sec. Find the head lost due to friction and power required to maintain the flow for a length of 1000m. Take v = 0.29 stokes.
Given data:
Specific gravity of oil (s) = 0.8
Diameter of pipe (d) = 300mm = 0.3m
Discharge (Q) = 450 lit/sec = 0.45 m3/sec
Lenght of pipe (L) = 1000m
Kinenatic viscisity (v) = 0.29 stokes = 0.29 × 10-4 m2/s
To find:
(i) Loss of head due to friction (hf)
(ii) Power Required (p)
Solution:

Result:
(i) Head loss due to friction (hf) = 135.97m
(ii) Power required (P) = 480.18 kw
Example - 49
Calculate the discharge through a pipe of diameter 200mm when the diffeference in pressure head between the two ends of a pipe 450m a part is 4m of water. Take the value of f = 0.009 in the formula 
Given data:
Diameter of pipe (d) = 200mm = 0.2m
Length of the pipe (L) = 450m
Difference of pressure head (hf) = 4m of water
Co-efficient of friction (f)= 0.009
To find:
Discharge (Q)
Solution:

Result:
Discharge (Q) = 30.9 lit/sec.
Example - 50
Water is flowing through a pipe of diameter 250mm with a velocity of 3 m/s. Find the loss of head due to friction for a length of 5m, if the co-efficient of friction is  Take kinematic viscosity of water is 0.01 stoke.
Take kinematic viscosity of water is 0.01 stoke.
Given data:
Diameter of pipe (d) = 200mm = 0.2m
Velocity (V) = 3m/s
Length (L) = 5m
Kinematic viscosity (v) = 0.01 stoke = 0.01 × 10-4 m2/s
To find:
Loss of head due to friction.
Solution:

Result:
Loss of head due to friction (hƒ) = 993 m of water
Example - 51
An oil of specific gravity 0.8 and viscosity of 0.05 poise is flowing through a pipe of diameter 200mm at the rate of 60 lit/sec. Find the head lost due to friction for a 475m length of pipe. find the power required to maintain this flow.
Given data:
specific gravity of oil (S) = 0.8
Viscosity of oil (μ) = 0.05 poise = 0.005 Ns/m2
Diameter of pipe (d) =200mm = 0.2m
Discharge (Q)=60 lit/sec = 60 × 10-3 m3/sec
= 0.06 m3/sec
Length of the pipe (L) = 475m
To find:
(i) Head loss due to friction (hƒ)
(ii) Power required.
Solution:

(iii) Head loss due to friction (hƒ)
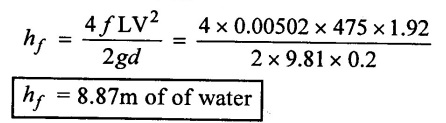
(iv) power Required (P)

Result:
P = 4.175 kw
(i) Head lost due to friction (hƒ ) = 8.87m of of water
(ii) Power required (P) = 4.175 kw.
Example - 52
Find head loss when a pipe of diameter 20cm. is suddenly enlarged to a diameter 40m. The rate of flow of water through the pipe is 200 lit/sec.
Given data:
Diameter of small pipe d1 = 20 cm = 0.2m
Diameter of large pipe d2 = 40 cm = 0.4m
Discharge through pipe (Q) = 200 lit/sec
= 0.2 m 3/sec
To find:
Head loss due to sudden enlargement (hc)
Solution:

Result:
Loss of head due to sudden enlargement he = 1.16 m of water
Example - 53
At a sudden enlargement of water main from 25cm to 50cm diameter, the hydraulic gradient rises by 12mm. Calculate the rate of flow through pipe.
Given data:
Diameter of small pipe (d1) = 25cm = 0.25m
Diameter large pipe (d2) = 50cm = 0.5m
Hydraulic gradient 
To find:
Rate of flow (Q)
Solution:

(ii) Loss of head due to sudden enlargement (he)

(iii) Applying Bernoullis equation

(iv) Discharge (Q) = A1 × V2 = A2 V2
= A2 = V2
= 0.196 × 0.198
= 0.0388 m3/s
(Q) = 38.84 lit/sec
Result:
Rate of flow (Q) 38.84 lit/sec
Example - 54
The rate of flow of water through a horizontal pipe is 0.25 m2/s. The diameter of the pipe which is 18 cm is suddenly enlaged to 36cm. The Intensity of pressure in the small pipe is 12 N/m2. Determine
(i) Loss of head due to sudden enlargement
(ii) Pressure intensity in the large pipe
(iii) Power lost due to enlargement.
Given data:
Rate of flow (Q) = 0.25 m3/s d1
Diameter of small pipe (d1) = 18cm = 0.18m
Diameter of large pipe (d2) = 36cm = 0.36m
Pressure intensity in small pipe (P1) = 12 N/m2
To find:
(i) Loss of head due to sudden enlargement (he)
(ii) Pressure intensity in the large pipe (P2)
(iii) Power lost due to enlargement (P)
Solution:

(v) Using Bernoulli's equation

(vi) Power lost due to enlargement (P)

Result:
(i) Loss of head due to sudden enlargement (he) = 2.78m of water
(ii) Pressure intensity in the large pipe (P2) = 16.818 N/m2
(iii) Power lost due to enlargement(P) = 6.82 kw
Example - 55
Oil of specific gravity 0.80 flows in a 100mm diameter pipe line. A sudden expansion takes place into a second pipe line of such a diameter that maximum pressure rise is obtained. If the oil flow rate in the pipe line is 20 lit/sec, Find the loss of head due to sudden expansion.
Given data:
Specific gravity of oil (S) = 0.8
Diameter of pipe (d1) = 100mm = 0.1m
Discharge (Q) = 20 lit/sec = 0.02 m2/s
To find:
Head loss due to sudden enlargement (he)
Solution:
(i) Q = A1 V1 = A2 V2

(ii) Diameter for maximum pressure rise,

(iii) Head loss due to sudden enlargement
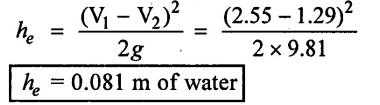
Result:
Head loss due to sudden enlargement (he) = 0.081m of water
Example - 56
A horizontal pipe of diameter 400mm is suddenly contracted to a diameter of 200mm. The pressure intensities in the large and smaller pipe is given as 14 N/ m2 and 12 N/m2 respectively. Find the loss of head due to contraction if Cc = 0. 62. Also determine the rate of flow of water.
Given Data:
Diameter of large pipe (d1) = 400mm = 0.4m
Diameter of small pipe (d2) = 200mm = 0.2m
Pressure intensity at large pipe (P1) = 14 N/cm2 ⇒ P1 = 14 ×104 N/m2
Pressure intensity at small pipe (P2) = 12 × 104 N/m2
co-efficient of contraction (Cc) = 0.62
To find:
(i) Loss of head due to contraction (he)
(ii) Rate of flow of water (Q)
Solution:

(iii) By using continuity equation
Q = A1 V1 = A2 V2

(iv) Head loss to sudden contraction

(v) Apply Bernoullis equation

Apply the value of V2 in equation (i) we set,
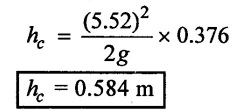
(vi) Rate of flow
Q = A1 V1 = A2 V2
Q = A2 × V2 = 0.0314 × 5.52
Q = 0.1733 m2/s
Q = 173.3 lit/sec
Result:
Loss of head due to contraction (hc) = 0.584m
(ii) Rate of flow (Q) = 173.3 lit/sec
Example - 57
A horizontal pipe of diameter 400mm is suddenly contracted to pipe diameter of 200mm. The pressure intensities in the large and smaller pipe given as 18 N/m2 and 12 N/cm2 respectively. Find the loss of head due to contraction if rate of flow of water is 300 lit/sec. Find the value of co-efficient of contraction. (Cc).
Given data:
Diameter of large pipe (d1) = 400mm = 0.4m
Diameter fo small pipe (d2) = 200mm = 0.2m
Pressure intensity at large pipe (P1) = 18 N/cm2 = 18 × 104 N/m2
Pressure intensity at small pipe(P2) = 12 N/vm2 = 12 × 104 N/m2
Rate of flow (Q) = 300 lit/sec = 0.3 m3/sec
To find:
Co-efficient of contraction (Cc).
Solution:

(iii) By using continuity equation Q = A1 V1 = A2 V2

V2 = 9.55 m/s
(iv) Applying Bernoulli's equation.

18.34 +0.29 - 12.23 - 4.65 = hc.
hc = 1.76 m of water
(v) Loss of head due to sudden contraction hc,
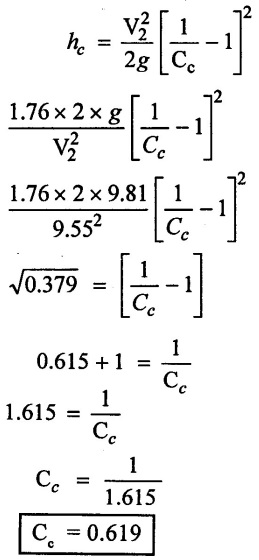
Result:
Co-efficient of contraction (Cc) = 0.619
Example - 58
A 150mm diameter pipe reduces in diameter abruptly to 100mm diameter. If the pipe carries water at 30 lit/sec. Colculate the pressure loss across the contracion. Co-efficient of contraction as 0.6.
Given data:
Diameter of large pipe (d1) = 150mm = 0.15m
Diameter of small pipe (d2) = 100mm = 0.1m
Discharge (Q) = 30 lit/sec = 0.03 m3/sec
co-efficient of contraction Cc = 0.6
To find:
Pressure loss (P1 − P2)
Solution:

(iv) By using Berboulli's equation,
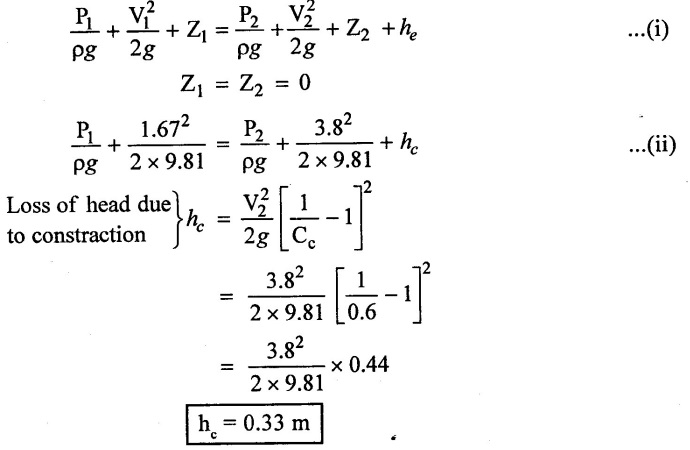
Apply the value of h in equation (ii)

Result:
Pressure loss across contraction (P1 - P2) = 0.906 × 104 N/m2
(P1 - P2) = 0.906 N/cm2
Example - 59
A sudden enlargement is introduced in a horizontal pipe line from 150mm diameter to 300mm diameter. Measurements indicate that when from is smaller to larger cross-section, the head loss is 0.6m in excess of that when the flow takes place from larger to smaller section. Determine the flow rate. the coefficient of contraction as 0.62.
Given Data:
Pipe Diameters d1 = 150mm = 0.15m
d2 = 300mm= 0.3m
hc − hc = 0.62
co-efficient of contraction (Cc) = 0.62
To find:
Rate of flow (Q)
Solution:
(i) Apply continuity equation
Q = A1 V1 = A2 V2

(ii) Head loss due to sudden expansion

(iii) Head loss due to sudden contraction

(iv) he - hc = 0.6 (Given)

(iv) Flow rate Q1 = A1 V1 = 0.0177 × 7.89
Q = 0.139, 653 m3/sec
Q = 139.653 lit/sec
Result:
Rate of flow (Q) = 139.653 lit/sec
Example - 60
Water is flowing through a horizontal pipe of diameter 200mm at a velocity of 2.5 m/s. A circular solid plate of diameter 120mm is placed in the pipe to obstruct the flow. Find the loss of head due to obstruction in the pipe if Cc = 0.6
Given Data:
Diameter of pipe (D) = 200mm = 0.2m
velocity (V) = 2.5 m/sec
Diameter of obstruction (d) = 120mm = 0.12m
Cc = 0.6
To find:
Loss of head due to obstruction (h0)
Solution:

(iii) Head loss due to obstruction (hob)
 Result:
Result:
Head loss due to obstruction hob = 0.819 m.
Example - 61
Determine the rate of flow water through a pipe of diameter 20cm and length 50m when one end of the pipe is connected to a tank and other end of the pipe is open to the atmosphere. The pipe is horizintal and the height of water in the tank is 4m above the centre of the pipe. Consider all minor losses and take f = 0.009 in the formula 
Given data:
Diameter of pipe (d) = 20cm = 0.2m
Length of pipe (L) = 50m
Height of water (H) = 4m
Co-efficient of friction ƒ = 0.009
To find:
Rate of flow (Q)
Solution:
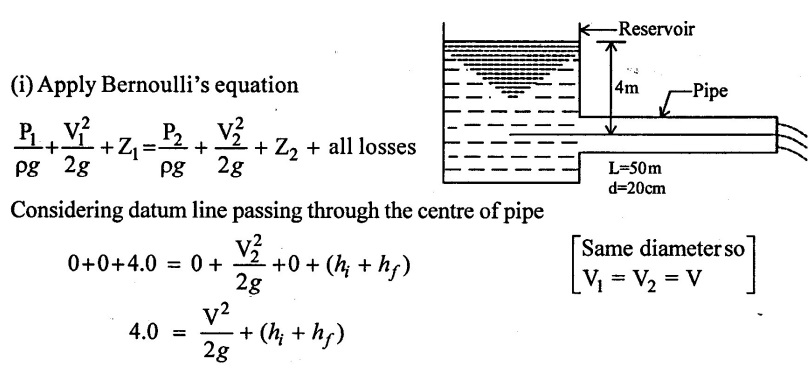
We. know that

(ii) Rate of flow (Q)

Q = 0.08589 m3/s
Q = 85.89 lit/sec
Result:
Rate of flow (Q) = 85.89 lit/sec
Example - 62
Determine the difference in the elevations between the water surfaces in the tanks which are connected by a horizontal pipe of diameter 300mm and length 400m. Take rate of flow of water through the pipe is 300 lit/s. Consider all losses and take the value of ƒ = 0.008.
Given data:
Diameter of pipe (d) = 300mm = 0.3m
Length (L) = 400m
Discharge (Q) = 300 lit/sec = 0.3 m3/sec ⸫ Z1 = Z2 = 0
Co-efficient of friction (f) = 0.008
To find:
Diffrence in elevations
Solution:
 Substituting these value in equation (i) we set,
Substituting these value in equation (i) we set,
H1 = H2 + 0.459 + 39.16 + 0.918
H1 - H2 = 40.537m
Result:
Difference in Elevations (H1 – H2) = 40.537m.
Example - 63
A pipe line AB of of diameter 300mm and of length 400m carries water at the rate of 50 lit/sec. The flow takes place from A to B where point B is 30 metre above A. Find the pressure at A if the pressure at B is 19.62 N/cm2. Take ƒ = 0.008.
Given data:
Diameter of pipe (d) = 300mm = 0.3m
Length of pipe (L) = 400m
Discharge (Q) = 50 lit/sec = 0.05 m3/sec
Pressure at B = (PB) = N/cm2 = 19.62 × 104 N/m2.
ƒ = 0.008
To find:
Pressure at A.
Solution:

Applying Bernoulli's equation at points A and B taking datum line passing through A, We have

Result:
Pressure at A = 50.1192 N/cm2
Example - 64
For sudden expansion in a pipe flow, work output the optimum ratio between the diameter of the pipe before expansion and the diameter of pipe after expansion. so that pressure rise maximum? Also find the maximum pressure rice.
To find:
(i) Diameter ratio for the maximum pressure rise
(ii) Maximum pressure rise
Solution:
(i) Apply Bernoulli's Equation
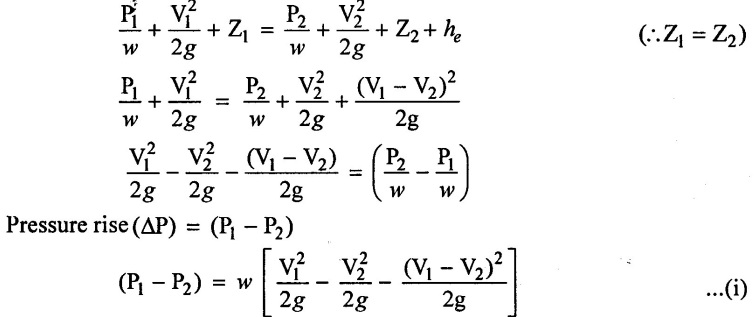
(ii) By using continuity equation
A1 V1 = A2 V2

Apply the value of n equation (i)

Diameter ratio for the maximum pressure rise
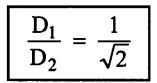
(2) Maximum pressure raise (ΔP)max

Result:

No comments:
Post a Comment