Euler's Equation

 Flow is under steady state i.e, mass flow rate of fluid at any point on the rotor is constant.

EULER'S EQUATION

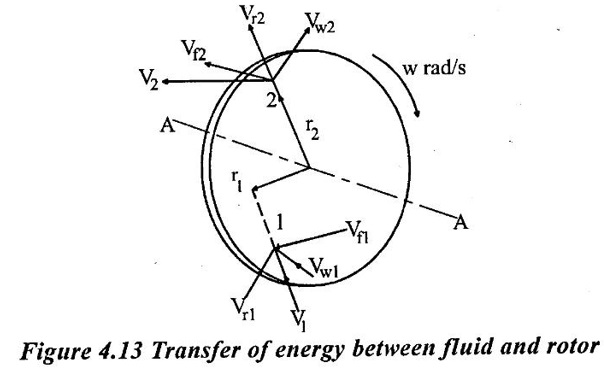
Consider a rotor rotating at an angular speed of w rad/s as shown in figure. 4.13. 

Consider two points 1 and 2 on the rotor at radii r1 and r2. Assume that the fluid enters at point 1 and leaves at point 2.

Assumptions:

1. Flow is under steady state i.e, mass flow rate of fluid at any point on the rotor is constant.

2. The state of the fluid at any given point is constant i.e, the rate of heat and work transfer by the fluid passing on-the rotor is constant.

3. There is no leakage of fluid of any point and the entire fluid is undergoing the same process.

4. There are no frictional losses as the fluid flows over the own through the rotor.

Note that the transfer of energy between fluid and machine only depends upon the dynamic condition of fluid at points 1 & 2 and it is independent of the actual path followed by the fluid.

Let, m = Mass flow rate of fluid in kg/s

V1 = Absolute velocity of fluid at point 1 in m/s

V2 = Absolute velocity of fluid at point 2 in m/s

ω = Angular velocity of rotor in rad/s

Resolving the absolute velocity in axial, radial and tangential direction, we can writs

V1 =Vƒ1 + Vr1 + Vw1

V2 = Vƒ2 + Vr2 + Vw2

The energy transfer between the fluid & machines is only due to change in momentum caused by the tangential component of velocity. Therefore.

The rate of change of momentum between point 1 & 2,

= m Vw1 - m Vw2

The moment of momentum at point 1 = m Vw1 •r1

The moment of momentum at point 2 = m Vw2• r2

Since the rate of change of moment of momentum represents the rate of change of angular momentum which is equal to torque produced on the rotor Hence,

Torque T = Rate of change of angular momentum,

T = m Vw1 •r1 - m Vw2• r2

T = m (Vw1 •r1 − Vw2• r2)                 ...(i)

In case of power producing machines like turbine the torque is produced on the rotor due to change of angular momentum. While in case of power absorbing devices like pumps and compressor, the torque given to the rotor is responsible for causing the change in tangential velocity of fluid.

Example:

Consider the machine as turbine.

The torque produced by the fluid on rotor is used in producing useful work or developing power. Thus,

Rate of energy transfer or power P

E = Torque (T) × Angular velocity of rotor ω

E = T.ω

E = (Vw1r1 − Vw2r2) × ω                ...(ii)

But peripheral velocity of fluid, (u = ωr) at points 1 and 2 can be written as,

u1 = ω • r1 and u2 = ω • r2

⸫ E = m(V w1 •u1 − V w2 •u2)           ...(iii)

The equation (iii) represents the general energy equation for tranfer of energy between the fluid and machine.

Energy tranfer per unit mass (i.e) work done/sec

E or W = (Vw1 •u1 - V w2 •u2)            ...(iv)

If H is the head on the machine, then energy transfer can be written as,

E = m.g.H                                      ...(v)

Equating the equation (iii) & (v)

The equation (ii) to (vi) are forms of Euler's equation which are applicable to all turbomachines.

Note:

(i) If Vw1 u1 > Vw2 u2, then machine is called turbine

(ii) If Vw2 u2 > Vw1 u1 then machine is called a pump or compressor

(iii) If Vw2 is in opposite direction of vwl, the equation (i) can be modified-as,

E = m(Vw1 u1 + Vw2 u2)