Unit III: Dimensional Analysis and Model Studies - Previous Year Anna University Solved Problems

Problem - 1

The pressure different AP in a pipe of diameter (D) and length (1) due to viscous flow depends on the velocity (V) viscosity (μ) and density (ρ). Using Buckingham's π- theorem obtain an expression for ΔP.

Given data:

Pressure difference ΔP depends on the

Diameter (D)

Length (l)

Velocity (V)

Viscosity (μ)

Density (ρ)

To find:

Expressing the functional equation for ΔP.

Solution:

Pressure difference (ΔP) = ML-1T-2

Diameter (D) = L

Length (l) = L

Velocity (V) = LT-1

Viscosity (μ) = ML-1T-1

Density (ρ) = ML-3

Step - 1 Write the functional equation

ΔΡ = f (D, l, V, μ, ρ)

Also can be written as

f1 (ΔP, D, l, V, μ, ρ) = 0

Step - 2 Findout number of π- terms.

Total number of variables (n) = 6 

Fundamental dimensions (m) = 3

Number of π-terms = n – m = 6 – 3 = 3

Hence,

f1 (π1, π2, π3) = 0             ...(1)

Step - 3 Select the repeating variables. 

Geometric property = Diameter (D)

Flow property = Velocity (V)

Fluid property = Density (ρ)

⸫ Repeating variables = D, V, ρ

Step - 4 Write the all π - terms with arbitary powers

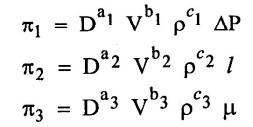
Step - 5 Findout all the arbitary powers values of each л terms using dimensional homogeneity.

Step - 6 Apply the values of π1, π2 & π3 in equation - (1)

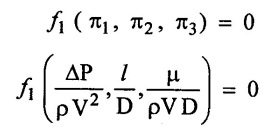
Step - 7 Expressing any one of the л-term as a function of others with constant ϕ

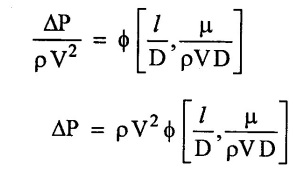
Result:

Functional Equation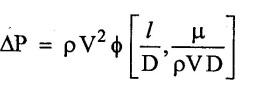

Problem - 2

Oil moved up in a lubricating system by a rope dipping in sump containing oil and moving up. The Quantity of oil pumped Q, depends upon the speed (u) of the rope, the layer thickness δ, the density and viscosity of the oil and acceleration due to gravity obtain the dimensionless parameters to correlate the flow.

Given data:

Discharge (Q) depends upon

Speed (u)

layer thickness (δ)

density (ρ)

viscosity (μ)

acceleration (g)

To find:

Derive the functional equation using Rayleigh's Ritz method.

Solution:

Q = L3T-1

u = LT-1

δ = L

ρ = ML-3

μ = ML-1T-1 

g = LT-2

Step - 1 Write the functional equation.

Q = ƒ (u, δ, ρ, μ, g)

Step - 2 Write the functional equation with constant and arbitary powers a, b, c...z

Step - 3 Find the values of arbitary powers.

Apply MLT system in equation (1) on both sides.

L3T-1 = k [(LT-1)a‚(L)b, (ML-3)c, (ML-1T-1)d,(LT-2)e]

Power of M

0 = c + d            ...(2)

Power of L

3 = a + b -3c - d + e             ...(3)

Power of T

-1 = a – d - 2e                        ..(4)

There are five unknowns in the above equations. So express the three unknowns interms of other two unknowns which are important. viscosity and gravity are more important in this problem. Hence expressing a, b, are c interms of d & e.

From equation – (2)

0 = c + d

C = - d

From equation - (4)

-1 = -a – d - 2e

a = - d - 2e + 1

From equation - (3)

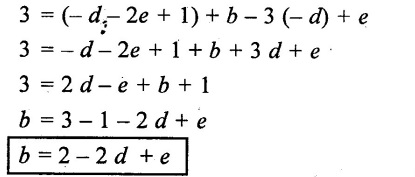
Step - 4 a, b, & c values are apply in equation (1)

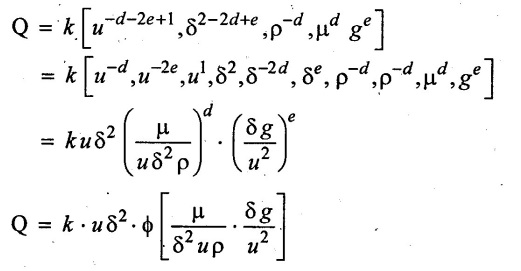
Result

Functional equation Q =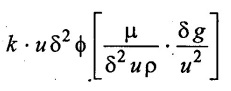

Problem - 3

Expressing the efficiency in terms of dimensionless parameters using density, viscosity, angular velocity, diameter of the rotor and discharge using Buckingham's  π - theorem.

Given data:

Efficiency (η) depends on

Density (ρ)

Viscosity (μ)

angular velocity (ω)

Diameter (D)

Discharge (Q)

To find:

Express the functional equation

Solution:

η = M°L°T° 

ρ = ML-3

μ = ML-1T-1

ω = T-1

D = L

Q = L3T-1

Step - 1 Write the functional equation

η = ƒ (ρ, μ, ω, D, Q)

Also can be written as

f1 = (η, ρ, μ, ω, D, Q) = 0

Step - 2 Find out the number of π – terms

Number of π - terms = n - m

= 6 - 3 = 3

So,

f1 = (π1, π2, π3) = 0                  ...(1)

Step - 3 Select Repeating variables

Geometric property = Diameter (D) 

Flow property = Angular velocity (ω) 

Fluid property = Density (ρ)

⸫ Repeating variables (D, ω, ρ)

Step - 4 Write the each л terms with aribitary power

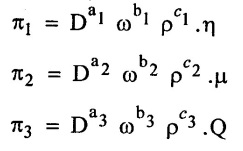
Step - 5 Find out aribitary values for each л - terms.

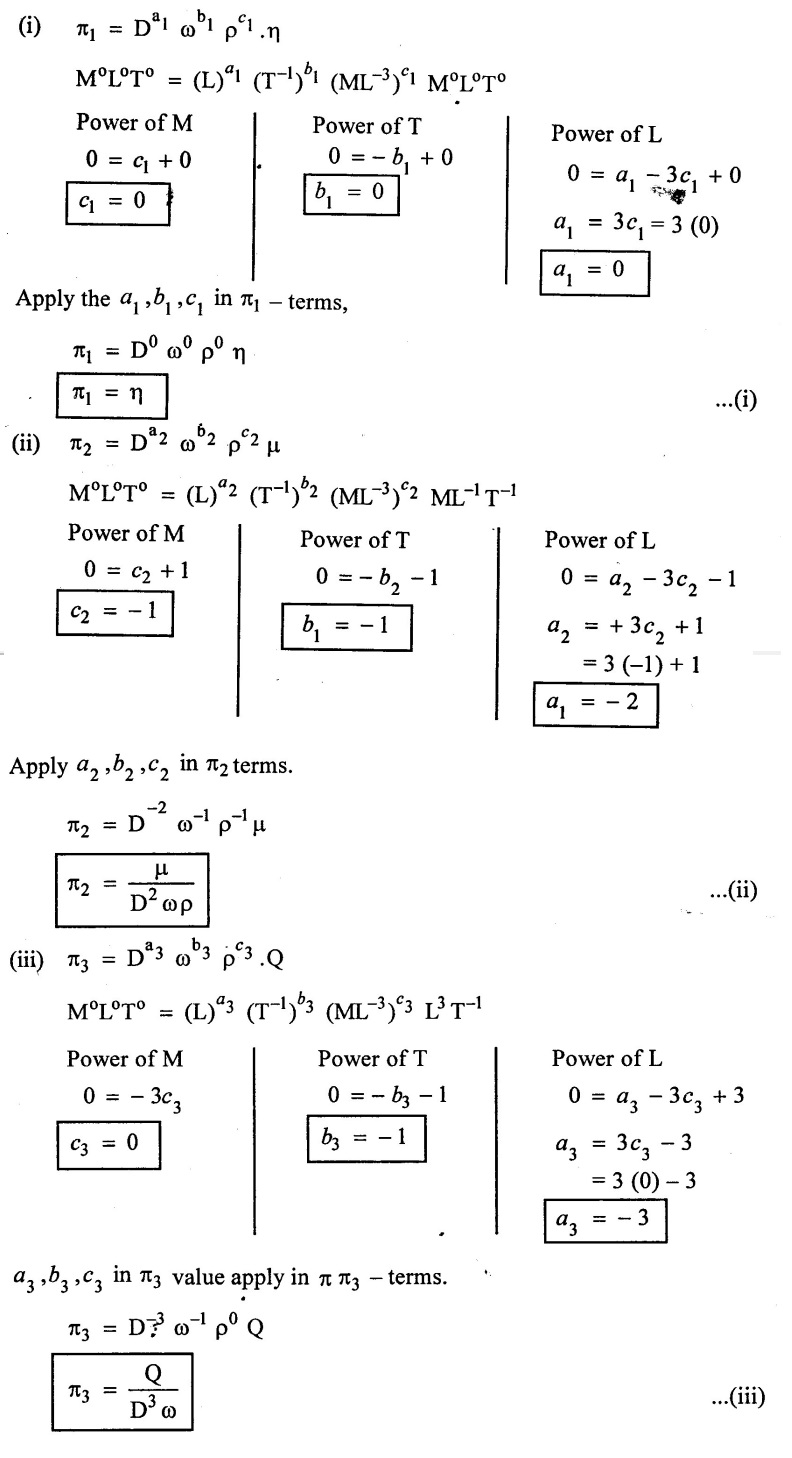
Step - 6

Apply the values of π1, π2, π3 values in equation (1)

f1 (π1, π2, π3) = 0

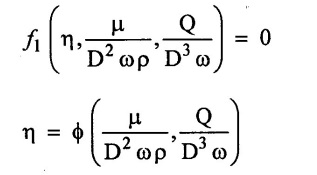
Result

Problem - 4

Using Bucking ham's л theorem show that the velocity through circular pipe orifice is given by 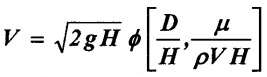where H – head casting flow, D - Diameter of orifice, μ co-efficient of viscosity, ρ - mass density, g - acceleration due to gravity.

This problem is same as Example - 13 in Page no: 3.35

Problem - 5

Derive on the basis of dimensional analysis suitable parameters to present the thrust developed by a propeller. Assume that thrust P depends upon the angular velocity (ω). Speed of Advance (u), Diameter (D), dynamic viscosity (μ), mass density (ρ), elasticity of fluid medium which can be denoted by the speed of sound in the medium (C).

This Problem is same as Example 16 in Page no: 3.45

Problem - 6

Using dimensional analysis obtain a correlation for frictional torque due to rotation of disc in a viscous fluid. The parameters influencing the torque can be identified as the diameter, rotational speed, viscosity and density of fluid. The frictional torque (T) of a disc diameter of fluid (D), rotating speed (N) in fluid of viscosity (μ) and density (ρ) in a turbulent flow is given by 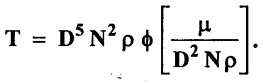Prove it by Bucking ham's л – theorem. 

This problem is same as Example - 15 in Page no: 3.42

Problem - 7

The drag force on a smooth sphere is found to be affected by the velocity of flow (V), the diameter (D) of the sphere and fluid properties density (ρ) and viscosity (μ). Find the dimensionless groups to correlate parameters. 

This problem is same as Example – 04 in Page no: 3.14

Problem - 8

The efficiency (η) of a fan depends on density (ρ), viscosity (μ) of the fluid, angular velocity (ω) diameter (D) of the rotor and discharge (Q). Express efficiency (η) in terms of non – dimensional parameters, use Bucking ham's π theorem 

This problem is same as university solved problem - 3 in Page no: 3.121.

Problem - 9

The resisting force F of a plane during flight can be upon the length of aircraft (l), velocity (V), air viscosity (μ), air density (ρ) and bulk modulus of air (k). Express the functional relationship between these variables using dimensional analysis 

This problem is same as Example- 18 in Page no: 3.52

Problem - 10

The drag force (F) on a partially submerged body depends on relative velocity (V) between the body and fluid length (l), height of surface roughness (k), fluid density (ρ), viscosity (μ) and acceleration due to gravity (g) obtain expression for drag force, using method of dimensional analysis

Given data:

Drag force (F) depends on

Relative velocity (V)

Length (l)

Surface roughness (k),

density (ρ)

viscosity (μ)

acceleration due to gravity (g).

To find

Derive the functional equation

Solution:

Drag force (F) = MLT-2 

velocity (V) = LT-1

Length (l) = L

Surface roughness (k) = L

density (ρ) = ML-3

viscosity (μ) = ML-1T-1

gravity (g) = LT-2

Step - 1 Write the functional equation

F = ƒ (V, l, k, ρ‚ μ‚ g)

Also can be written as,

f1 = (F, V, l, k, ρ‚ μ‚ g)

Step - 2 Find out the number of л - terms.

Total number of variables (n) = 7

Fundamental dimensions (m) = 3

number of π terms = n - 3

= 7 – 3 = 4

Hence,

f1 (π1, π2, π3, π4) = 0        ...(1)

Step - 3 Select repeating variables.

Repeating variables = l, V, ρ

Step - 4 Write the each л – terms with arbitary powers.

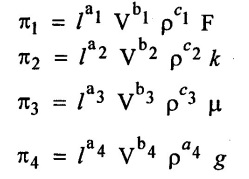
Step - 5 Find out the aribitary power values for each π - terms using dimensional homogeneous

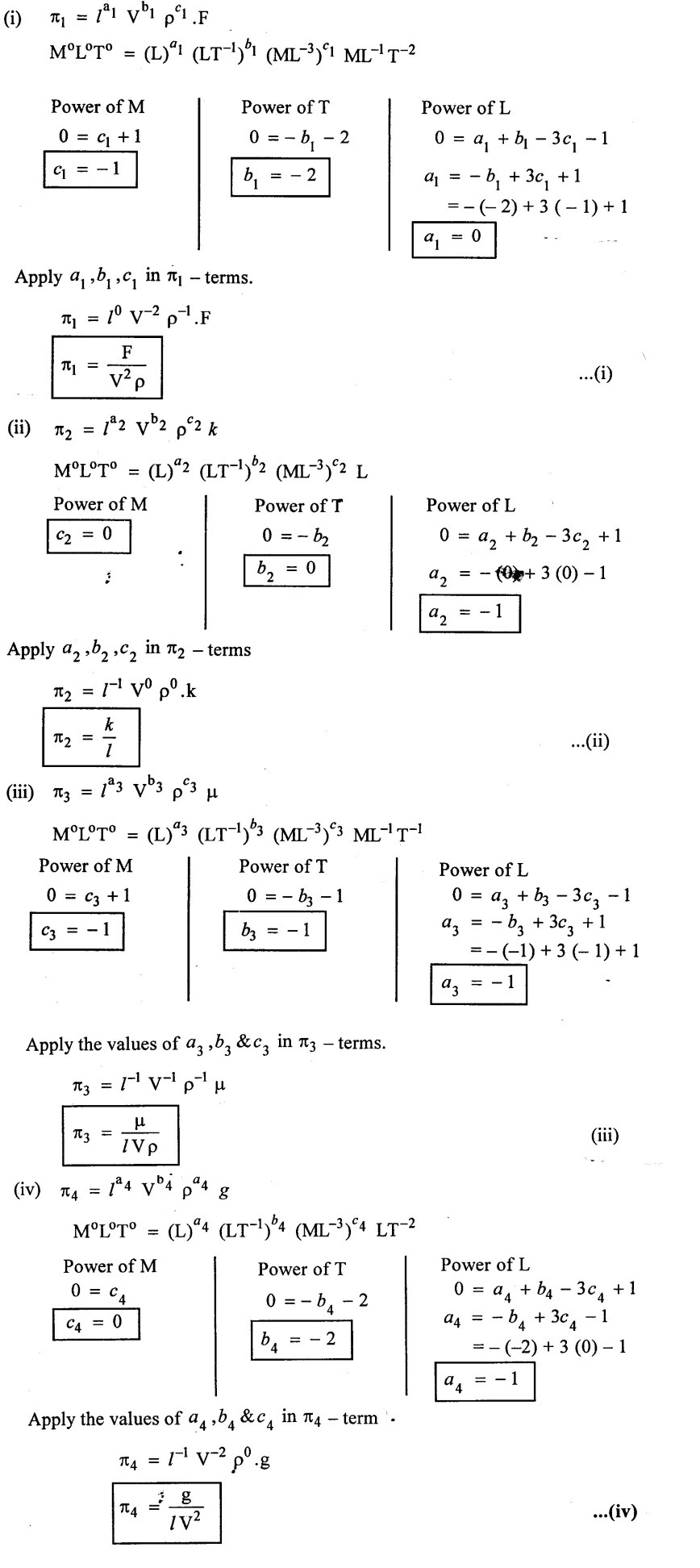
Step - 6 Apply the values of π1, π2, π3, π4 in equation – (1)

f1 (π1, π2, π3, π4) = 0

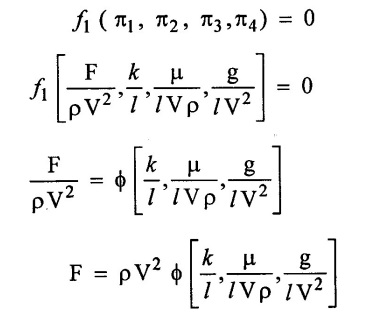
Result

Functional equation F =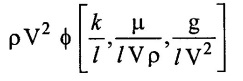

Problem - 11

An agitator of diameter D rotates at a speed N is a liquid of density ρ and viscosity μ, show that power required to mix the liquid is expressed by a functional form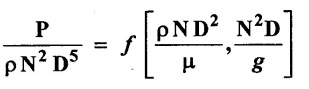

Given data

Power (P) depends on

Diameter (D)

Speed (N)

density (ρ)

viscosity (μ)

gravity (g)

To find

Show that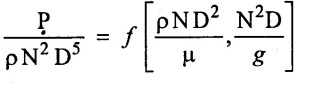

Solution:

Power (P) = ML2 T-3

Diameter (D) = L

Speed (N) = T-1

density (ρ) = ML-3

viscosity (μ) = ML-1T-1

gravity (g) = LT-2

Step - 1

Write the functional equation

P = ƒ (N, D, ρ, μ, g)

Also can be write as,

f1 (P, N, D, ρ, μ, g) = 0

Step - 2

To findout the number of л - terms.

Total number of variables (n) = 6

Number of fundamental variables (m) = 3

Number of л – terms = n – m

= 6 – 3 = 3

Hence,

f1 (π1, π2, π3) = 0

Step - 3

Select the repeating variables

Repeating variables = D, N, ρ

Step - 4

Write the each π- terms with aribitary powers.

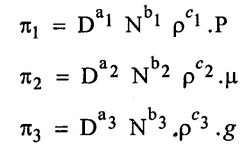
Step - 5

Find out the arbitary power values for each л - terms

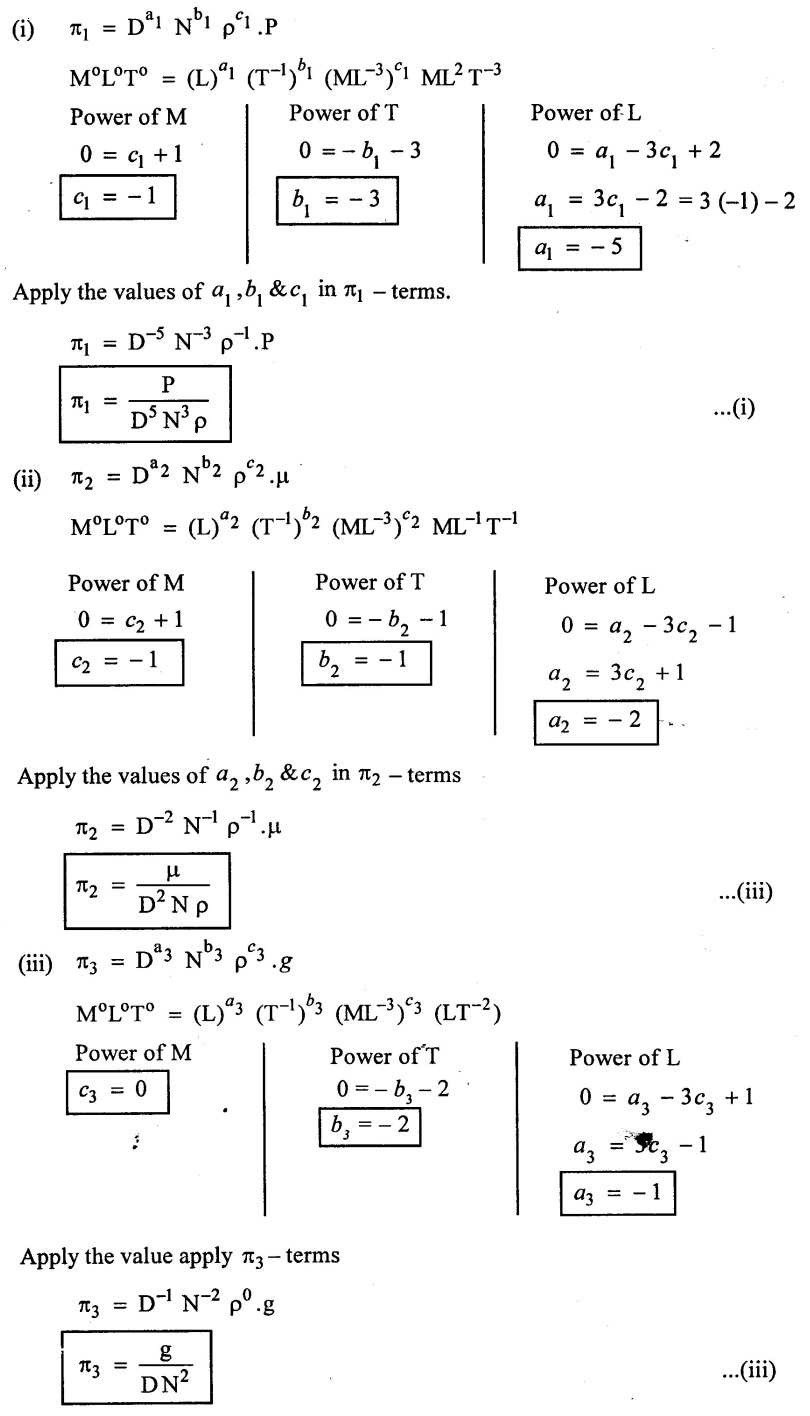
Step - 6

Apply π1, π2, π3 values in equation (1)

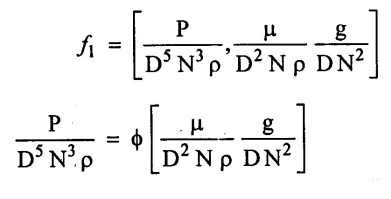
Inverse of π2 & π3 is also dimensionless term, replace

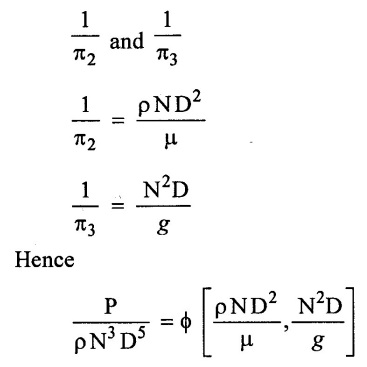
Result:

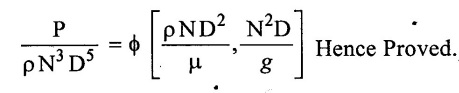
Problem - 12

The power developed by hydraulic machine is found to depends on head (h), flow rate (Q), Density (ρ), speed (N), runner diameter (D), and acceleration due to gravity (g), obtain the suitable dimensionless parameters to correlate the experimental results.

Given data:

Power (P) depends on

Head (h),

flow rate (Q),

Density (ρ),

Speed (N),

Diameter (D),

gravity (g),

To find

Derive the functional equation using Rayleigh Rits method.

Solution:

Power (P) = ML2 T-3 

Head (h) = L 

Density (ρ) = ML-3 

Speed (N) = T-1 

Discharge (Q) = L3 T-1

gravity (g) = LT-2

Diameter (D) = L

Step - 1

Write the functional equation.

P = f (h, Q, D, ρ, N, g)

Step - 2

Write the functional equation with arbitary powers and constant.

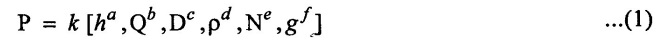
Step - 3

Find the value of arbitary powers

Apply MLT system in equation (1) on both sides.

There are five unknowns in the above equations. So express the two unknowns in terms the other three which are important. Head, discharge and gravity are more important is this problem. Hence expressing c & e interms of a, b, f.

From equation (2) => d = 1

From equation - (3)

c = 2 – a - 3b + 3d - f

= 2 – a - 3b + (3 × 1) − f

c = 5 – a - 3b - f

From equation – (4)

-3 = - b - e - 2f 

e = 3 – b - 2f

Step – 4    

c, d & e value applying equation – (1)

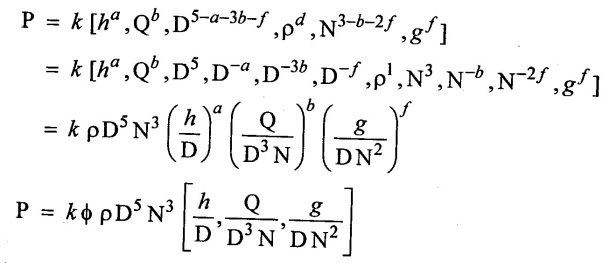
Result

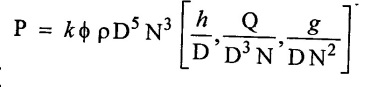
Problem - 13

The capillary rise (h) is found to be influenced by the tube diameter (D), Density (ρ), gravitational (g) and surface tension (σ). Determine the dimension lass parameters for the correlation of experimental results. 

Given data

Capillary rise (h) depends on

Diameter (D),

Density (ρ)

gravity (g),

surface tension (σ),

To find

Correlate the experimental results

Solution:

h = L

Ꭰ = L

ρ = ML-3

σ = MT-2

Step - 1

Write the functional equation based on given

h = f (D, ρ, g, σ)

Step - 2

Write the functional equation with arbitary power and constant.

Step - 3

Find the values of arbitary powers

Apply MLT system on both sides

Step - 4

Apply a, b & c value in equation (1)

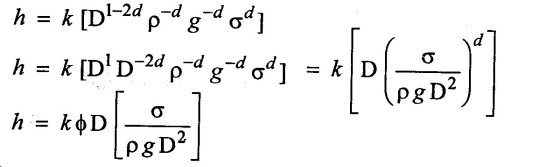
Result

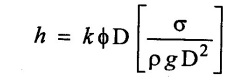
Problem - 14

Derive an expression for the shear stress at the pipe wall when in an incompressible fluid flows through a pipe under pressure. Use dimensional analysis with the following significant parameters pipe diameter (D), flow velocity (V), viscosity (μ) and mass density (ρ) of the fluid.

Given data

Shear stress τ depends on

Pipe diameter (D),

flow velocity (V),

Dynamic viscosity (μ),

and mass density (ρ)

To find

Derive the functional using Rayleigh's Ritz method.

Solution:

Step - 1

Write the functional equation.

τ = f (D, V, μ, ρ)

Step - 2

Write the functional equation with arbitary values and constant k 

τ = k (Da, Vb, μc, ρd)       ...(1)

Step - 3

To find out the aribitary values

Apply MLT system on both sides of the equation - (1)

ML-1T-2 = k [(L)a, (LT-1)b, (ML-1T-1)c, (ML-3)d]

There are four unknowns in the above equations. So express the three unknowns interms of other one unknowns which important property dynamic viscosity, hence expressing a, b, & d in terms of c.

From equation - (2)

d = 1 - c

From equation - (4)

-2 = - b - c

b = 2 - c

From equation (3)

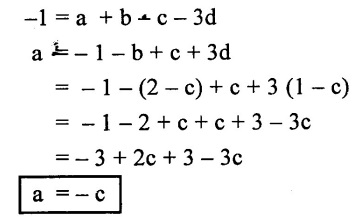
Step - 4

Apply a, b, & d value in equation (1)

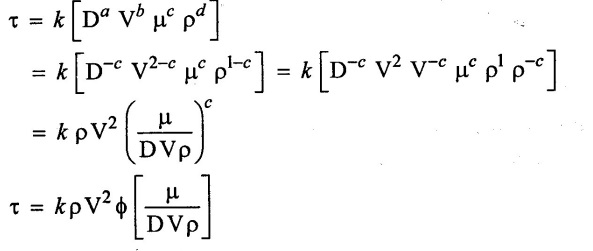
Result

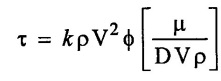
Problem - 15

Consider force Facting on the propeller of an aircraft which depends upon variables V, ρ, μ, D and N. Derive the non- dimensional functional form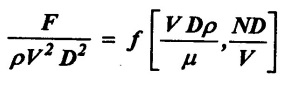

Given data

Force depends on

Density (ρ),

velocity (V),

Diameter (D),

Viscosity (μ),

Speed (N).

To find

Derive the functional equation.

Solution:

F = MLT-2

V = LT-1

ρ = ML-3

μ = ML-1T-1

D = L

LT-1

N = T-1

Step - 1 Write the functional equation

F = ƒ (V, ρ, μ, D, N)

also can be writen as,

f1 (F, V, ρ, μ, D, N) = 0

Step - 2 Findout number of π- terms

Number of л - terms = n - m

= 6 - 3

= 3

Hence

f1 (π1, π2, π3) = 0

Step - 3 Select repeating variables.

Repeating variables = D, V, ρ

Step - 4

Write each π- terms with arbitary powers.

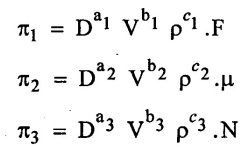
Step - 5

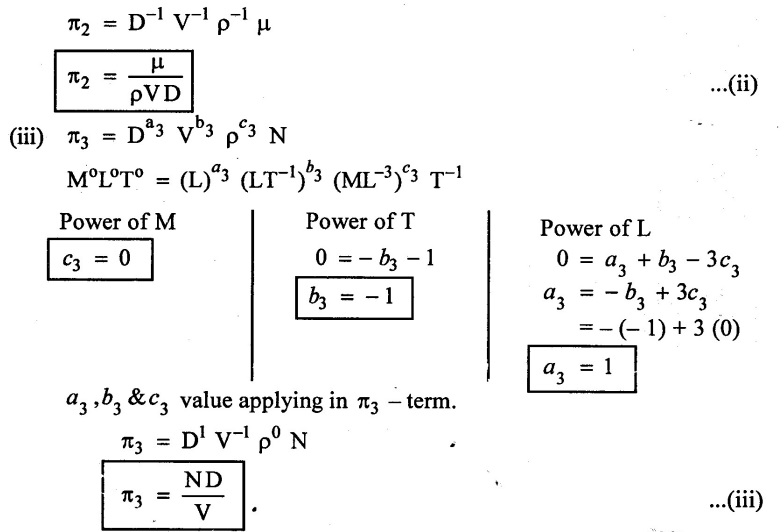
Findout arbitary values of each π – terms

Apply the values of а2, b2 & c2 in π2 – terms

Step - 6 π1, π2, π3 terms values are apply in equation (1)

f1 (π1, π2, π3) = 0

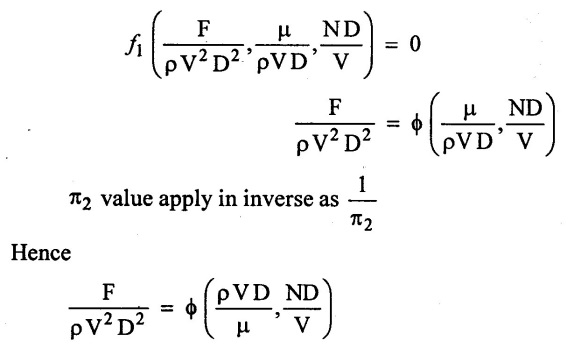
Result

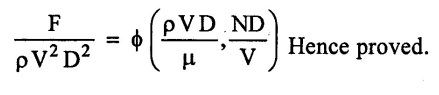
Problem - 16

The pressure difference ΔP in a pipe of diameter 'd' and length 'l' due to viscous flow depends on the velocity 'V' viscosity μ and density 'ρ' using Buckingham's л theorem, obtain an expression for ΔP. 

Given data:

Pressure difference ΔP depends on Diameter (D), length (l), velocity (V), viscosity (μ), and density (ρ).

To find:

Derive the functional equation.

Solution:

Step - 1

Write the functional equation.

ΔΡ = f (Δ, l, V, μ, ρ)

Also can be written as

f1 (ΔP, D, l, V, μ, ρ) = 0

Step -2: Find the number of л - terms

Number of л - terms = n − m

= 6 - 3

= 3

Hence

f1 (π1, π2, π3) = 0

Step 3: Select the Repeating variables

Repeating variables (l, V, μ)

Step 4: Write the each л - terms.

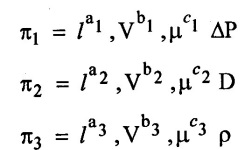
Step 5: Find out the aribitary values in each π- terms.

Step – 6 π1, π2, π3 value apply in equation (1)

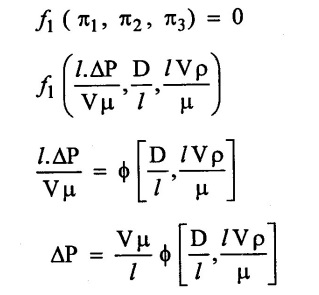
Result:

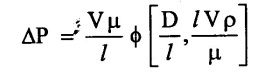
Problem - 17

State Buckingham's π - theorem. The discharge of a centrifugal pump (Q) is depends on speed (N) of pump, diameter (d) of impeller acceleration due to gravity (g), manometric head (H), ρ and μ are density and viscosity of fluid respectively. using dimensional analysis Buckingham's π - theorem. Prove that is given by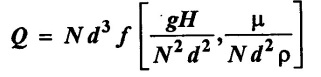  

Given data:

Speed of pump (N), Diameter (D), manometric head (H), viscosity (μ), Density (ρ) and gravity (g).

To find:

Derive the functional equation and show the Q =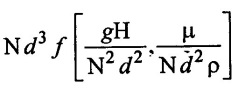

Solution:

Step -1

Write the functional equation

Q = ƒ (N, D, g, H, μ, ρ)

Also written as

f1 = (Q, N, D, g, H‚ μ‚ ρ) = 0 

Step 2:-

Number of π- terms = n - m

= 7 - 3

= 4

f1 (π1, π2, π3, π4) = 0

Step 3:-

Select the Repeating variables = D. N. ρ

Step 4:-

Write the each π- term with attribute values

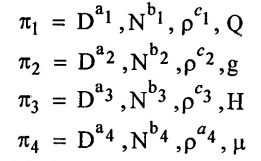
Step 5:

Find out attribute values of each ' π ' terms.

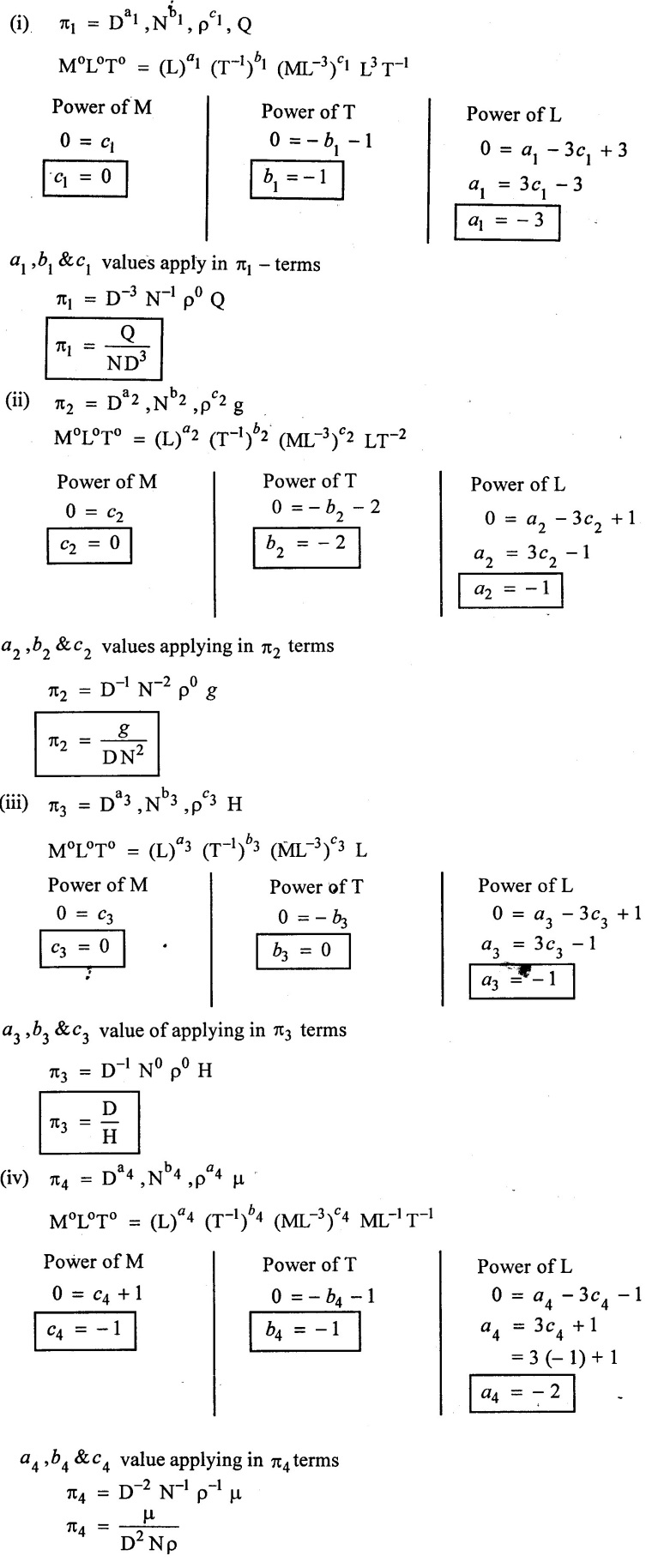
Step 6:- π1, π2, π3, π4 values applying in equation (1)

f1 (π1, π2, π3, π4) = 0

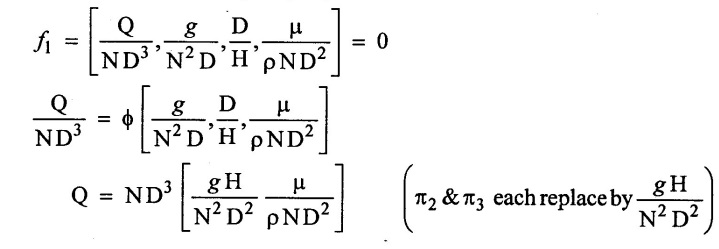
Result:-

Hence proved Q =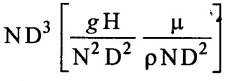

Problem - 18

The characteristics of spillway are to be studied by means of a geometrically similar model constituted to the ratio of 1:10

(i) If the maximum rate of flow in the prototype is 28.3 m3/s what will be the corresponding flow in model?

(ii) If the measured velocity in the model at a point on the spillway is 2.4 m/s. What will corresponding velocity in prototype?

(iii) If the energy dissipated per second in the model is 3.5 N.m.s. What energy is dissipated per second in the prototype?

(iv) If the hydraulic jump at the of the model is 50mm high, what will be the height of the jumping prototype? 

This problem is similar to Example No - 36 and Page No: 3.106.

Ans:

 (i) Discharge of model (Qm) = 0:0894m3 / s

(ii) Velocity of Prototype (Vp) = 7.589 m/s

(iii) Height of prototype (Hp) = 500mm

(iv) Energy dissipated of prototype (Ep) = 35000 Nm/s (or) watts.

Problem - 19

A geometrically similar model of spillway, the discharge per meter length is 0.2 m3/sec. If the scale of the model is 1/36. Find the discharge per meter length of the prototype.

This problem is similar to Example No-33 and Page No: 3.103.

Ans:

Discharge in prototype (Qp) = 1555.2 m3 / sec.

Problem - 20

A geometrically similar model of an air duct is built 1/25 the scale tested with water which is 50 times more viscous and 800 times more density of air. The tested under dynamically similar conditions, the pressure drop is 2 bar in the model. Find the corresponding pressure drop in the full scale prototype. 

Given data:

Model fluid = water. 

Prototype fluid = Air

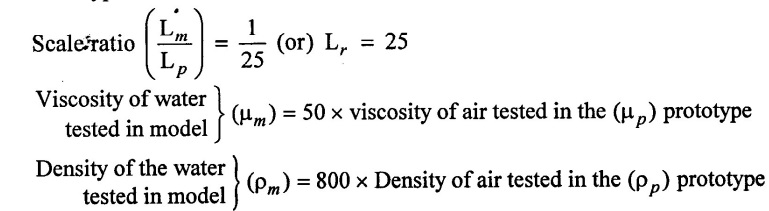
Pressure drop in model = 2 bar = 2 × 105 N/m2

To find: 

Pressure drop in Prototype (Pp)

Solution:

This problem involves pressure force and viscous force are dynamic similarity between model and prototype. So Euler's number and Reynold's number should be considered.

4) The Reynolds number should be equal for both model prototype

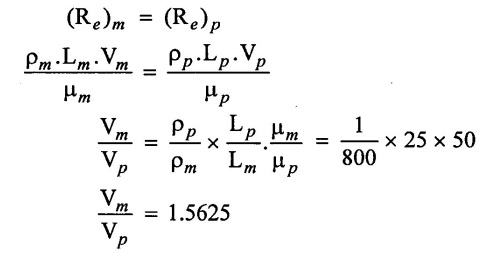
5) Euler's number is equal for both model and prototype

Result:

Pressure drop prototype (Pp) = 102.4 N/m2

Problem - 21

Water is flowing through a pipe of diameter 30cm at a velocity of 4 m/s. Find the velocity of oil flowing in another pipe of diameter 10 cm if the condition of dynamic similarity is satisfied between the two pipes. The viscosity of water and oil is given as 0.01 Poise and 0.025 poise the specific gravity of oil 0.8

Given data:

To find:

Velocity of pipe at 2 (V2)

Solution:

In this case closed pipe. So applied Reynold's model law.

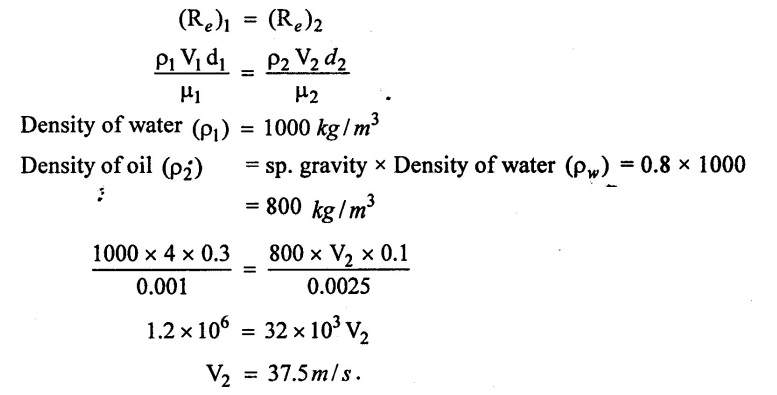
Result:

Velocity of pipe at 2 (V2) = 37.5 m/sec.

Problem - 22

Model tests have been conducted to study the energy loss in a pipeline of 1 m diameter required to transport kerosene of specific gravity 0.8 and dynamic viscosity 0.02 poise at the rate of 2000 l/s. If 10 cm diameter carries pipe water at 20° C, what is the flow rate in the model? If the energy head loss 30 m length at model is measured as 44.0 cm of water. What will be the friction factor for model?

Given data:

To find:

1. Discharge model (Qm)

2. Friction factor in prototype (Fp)

Solution:

3. Discharge model (Qm) = Am × Vm

Result:

1. Discharge model (Qm) = 0.07998 m3 / sec

2. Friction factor in prototype (F) = 2.774 × 10-4

Problem - 23

A pipe of diameter 1.5m is require to transport an oil of sp. gravity 0.9 and viscosity 3 × 10-2 poise at the rate of 3000 l/s test were conducted on 15 cm dia pipe using water at 20oC. Find velocity and rate of flow in model, if velocity of water at 20o c is 0.01 poise.

This problem is similar to Example No - 30 and Page No: 3.99.

Ans:

1. Velocity of model (Vm) = 5.085 m/sec.

2. Discharge of model (Qm) = 0.0899 m3/sec

Problem - 24

An oil of sp. gravity 0.92 and viscosity of 0.03 poise and 1.2 m diameter pipe. Model test were conducted on a 120 mm diameter pipe using water having viscosity of 0.01 poise. Find the velocity of flow and discharge in the model. 

This problem is similar to solved university problems No. 23 in Page no: 3.154.

Ans:

Velocity (Vm) = 6.78 m/sec

Discharge (Qm) = 0.1767 m3/sec

Problem - 25

A 7.2 m high and 15m long spillway discharge 94 m3/sec under a head of 2m. If a 1:9 scale model of this spillway is to be constructed. Determine the model law to be used model dimensions, head and discharge in the model. If model experties a force of 7500 N prototype,

This problem is similar to Example No - 37 and Page No: 3.108.

Ans:

(i) hm = 0.8m

(ii) Lm = 1.67m 

(iii) Hm = 0.222 m

(iv) Q m = 0.387 m3/sec

(v) Fp = 5.4675 × 106 N

Problem - 26

A spillway model is to built to geometrically similar scale of 1/50 across flume of 600mm width. The prototype is 15m high and maximum head on it is expected to be 1.5m.

1) What height of model and what head on model should be used?

2) If the flow rate over the model of a particular head is 12 liters per sec, what flow per rate length of the prototype is expected?

3) If the negative pressure in the model is 200 mm of water, what is negative pressure in prototype?

This problem is similar to Example No - 38 and Page No: 3.110.

Ans:

1. Height of model (hm) = 0.3 m

2. Head of model (Hm) = 0.03 m

3. Discharge/Length prototype Qp = 7.071 m3/sec/m

4. Negative pressure head prototype (hp) = − 10 m.

Problem - 27

In 1:30 model of a spillway velocity and discharge 1.5 m/sec and 2 m3 / sec. Find corresponding velocity discharge in the prototype.

Given data:

Scale ratio (Lr) = 30

Velocity of model (Vm) = 1.5 m/sec 

Discharge of model (Qm) = 2 m3 / sec

To find:

1. Velocity in prototype ratio (Vp)

2. Discharge of prototype (Qp)

Solution:

In this case for spill way so apply Froude's model law

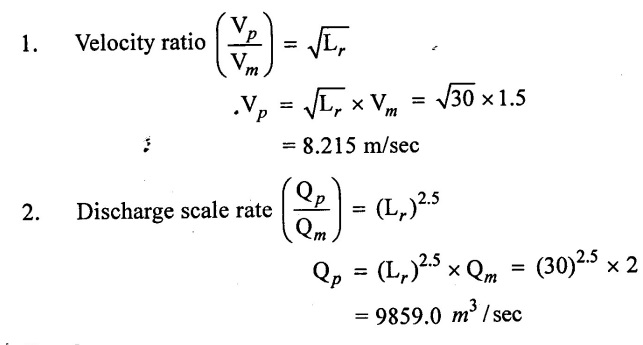
Result:

1) Vp = 8.215 m/sec

2) Qm = 9859.0 m3/sec