Solved Problems on closed systems (cyclic process)

 Solved Problems on closed systems (cyclic process): Basics, Zeroth and First Law - Engineering Thermodynamics

SOLVED PROBLEMS ON CLOSED SYSTEMS (CYCLIC PROCESS) 

Problem 1.1

During a flow process 5 kW paddle wheel work is supplied while the internal energy of the system increases in one minute as 200 kJ. Find the heat transfer when there is no other form of energy transfer.

Given data:

Work done, W = -5 kW (Since work is supplied to the system)

Internal energy, ΔU = 200 kJ/min = 200/60 = 3.33 kJ/s

To find:

Heat transfer, Q

Solution:

From first law of thermodynamics,

Q = W + ΔU

Q = -5 + 3.33 = -1.67 kW      Ans. ppp

(Note:- Negative sign indicates that the heat is transferred from the system.)

Problem 1.2

A liquid of mass 18 kg is heated from 25°C to 85°C. How much heat transfer is required? Assume Cp for water as 4.2 kJ/kg K.

Given data:

m = 18 kg

T1 = 25°C = 25 + 273 = 298 K

T2 = 85°C = 85 + 273 = 358 K

Cp = 4.2 kJ/kg K

To find:

Heat transfer, Q

Solution:

Heat transfer, Q = m Cp (T2 - T1)

Q = 18 × 4.2 × (358 - 298) = 4536 kJ      Ans. pp

Problem 1.3

A closed system receives an input heat of 450 kJ and increases the internal energy of the system for 325 kJ. Determine the work done by the system.

Given data:

Q = 450 kJ.

ΔU = 325 kJ

To find:

Work done, W

Solution:

By first law of thermodynamics,

Q = W + ΔU

450 = W + 325

W = 450 - 325 = 125 kJ               Ans.

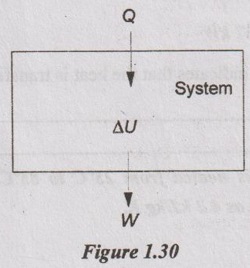
Problem 1.4

During the compression stroke of a reciprocating compressor, the work done to the air in the cylinder is 95 kJ/kg and 43 kJ/kg of heat is rejected to the surroundings. Determine the change in internal energy.

Given data:

W = -95 kJ/kg (Negative sign indicates that the work is done on the system)

Q = -43 kJ/kg (Since the heat is rejected from the system)

To find:

Change in internal energy, ΔU

Solution:

By first law of thermodynamics

Q = W + ΔU

- 43 = -95 + ΔU

ΔU = -43 - (-95)

ΔU = 52 kJ/kg             Ans.

Problem 1.5

Calculate the distance moved by a locomotive by consuming 2 tonne of coal if 10% of the heat generated by the coal is converted into coal gas then into mechanical work. The tractive effort required is 30 N/tonne of dead mass of the locomotive where the dead mass of the locomotive is 2500 tones. Assume 1 kg of coal liberating 35000 kJ of heat on burning.

Given data:

Mass of coal, mc = 2 tonne = 2000 kg

Available mechanical work, W = 10% of Q

Tractive effort = 30 N/tonne

Mass of the locomotive = 2500 tonnes

For 1 kg of coal, 35000 kJ of heat is generated. 

⸫ Calorific value of coal, CV = 35000 kJ/kg

To find:

Distance moved by a locomotive, x

Solution:

Heat generated,

Q = mc × CV = 2000 × 35000 = 70 × 106 kJ

Available mechanical work, W = 10% of Q = 10 / 100 × 70 × 106 = 70 × 105 kJ = 70 × 108 J

Total force required to move the locomotive,

F = Tractive effort/tonne × Dead mass in tonnes

= 30 × 2500 = 75000 N

We know that

Work done = Force, F × Distance, x

where

Work done is same as the available mechanical work.

70 × 108 = 75000 × x

⸫ x = 93333.3 m = 93.3 km          Ans.

Problem 1.6

The following data refer to a closed system which undergoes a thermodynamics cycle consisting of four processes.

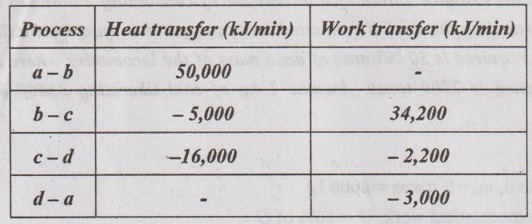
Show that the data is consistent with the first law of thermodynamics and calculate the

(a) Net rate of work output as MW

(b) Efficiency of the cycle.

Given data:

Qa-b = 50,000 kJ/min

Qb-c = -5,000 kJ/min

Qc-d = -16,000 kJ/min

Qd-a = 0

Wa-b = 0

Wb-c = 34,200 kJ/min

Wc-d = -2,200 kJ/min

Wd-a =-3,000 kJ/min

To find:

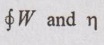
Solution:

The cyclic heat transfer of the cycle,

Similarly, the cyclic work transfer of the cycle,

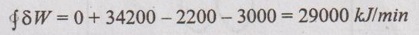
From the first law of thermodynamics,

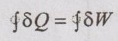
⸫ The given data is consistent with the first law of thermodynamics.

Problem 1.7

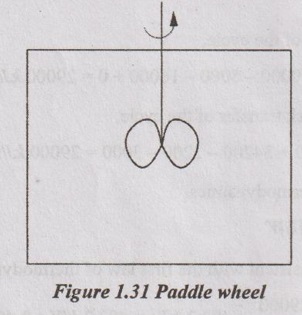
A paddle wheel fixed to a shaft of an engine revolves in a closed hollow vessel containing water. This closed vessel is connected freely on the shaft and restraint to its turning moment is proved by a mass attached to its side. Find the temperature rise for the following observations.

Engine rpm = 650

Load applied = 60 kg at a leverage of 1.2 m

Quantity of water = 200 kg

Duration of test = 20 minutes

Given data:

Speed, N = 650 rpm

Load, W = 60 kg = 60 × 9.81 = 588.6 N     [⸪ 1 kg = 9.81 N]

Leverage, l = 1.2 m

Mass of water, mw = 200 kg

Time, t = 20 minutes

To find:

Rise in temperature, Δtw

Solution:

Torque, T = W × l = 588.6 × 1.2 = 706.32 N-m

Brake power or work done,

= 2π NT × t = 2 π × 650 × 706.32 × 20 = 57693210 J

Heat gained by the water in 20 min,

Q = mw Cpw Δtw

57693210 = 200 × 4.18 × 103 × Δtw

[Cpw = 4.18 kJ/kg K = 4.18 × 103J/kg K]

Δtw = 69.01°C    Ans.

Problem 1.8

During a non-flow process, the temperature of the system changes from 15°C to 50°C. The work done by the system and heat transfer/°C rise in temperature at each temperature reached are given by

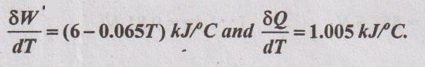
Determine change in internal energy of the system during the process.

Given data:

T1 = 15°C = 15 + 273 = 288 K

T2 = 50°C = 50 + 273 = 323 K

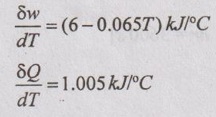
To find:

Change in internal energy, ΔU

Solution:

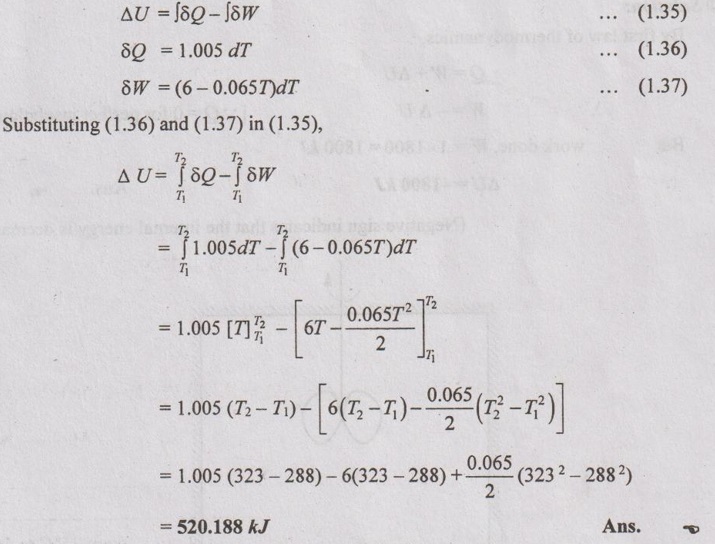
Problem 1.9

A 1 kW stirring motor is applied to a tank of water. The tank contains 15 kg of water and the stirring action is applied for 1/2 hr. If the tank is perfectly insulated, calculate the change in internal energy of the water, assuming that the process occurs at constant pressure and C, of water may be taken as 4.18 kJ/kgK. Also calculate the rise in temperature.

Missing 1.52 

Given data:

Power P 1 kW

Time, 1 1/2 hr = 0.5 x 3600 s = 1800 s

Mass of water, m = 15 kg

For perfect insulation, Q=0

C1 = 4.18 kJ/kg K

To find:

Change in internal energy, AU

Solution:

By first law of thermodynamics,

Engineering Thermodynamics

[·.· 1 hr = 3600 s]

Q=W+AU

W=-AU

Δυ

[Q=0 for perfect insulation]

:

But

work done, W= 1×1800= 1800 kJ

AU-1800 kJ

Ans.

(Negative sign indicates that the internal energy is decreased.)

Figure 1.32 Perfectly insulated tank with stirrer

For calculation, only magnitude is considered.

AU=mw Cv At

1800 = 15 x 4.18 x At

At 28.708°C

Ans.

Problem 1.10

During summer season, a room measuring 10 × 13 × 6 m3 is cooled electrically from initial temperature 28°C to 2°C. The air pressure inside the room is same as surroundings and is equal to 72 cm of Hg. The pressure remains constant during the cooling process. The cooling capacity of furniture and wall is 35 kJ/K. The specific heat of air is 1.005 kJ/kgK. Calculate the amount of electric energy needed for cooling the room. How much air comes out through gaps and windows during cooling period?

Given data:

Volume of air = 10 × 13 × 6 m3

T1 = 28°C = 28 + 273 = 301 K

T2 = 2°C = 2 + 273 = 275 K

Pressure = 72 cm of Hg

Cooling capacity of furniture and wall = 35 kJ/K

Cp of air = 1.005 kJ/kg K

To find:

The amount of electrical energy needed, E and the amount of air comes out during cooling, m

Solution:

We know that 76 cm of Hg = 1.013 bar

missing 1.54

Q1=907.4 x 1.005 (301 - 275) = 23710.36 kJ

Cooling effect required to cool the walls and furniture,

.. Total cooling effect, Electricity needed,

Q2-35 × (28-2) = 910 kJ

Q = Q1 + Q2 =23710.36+ 910 = 24620.36 kJ

е 3600 3600

24620.36

= 6.84 kW-hr

Ans.

Problem 1.11

25 people attended a farewell party in a small room of size 10 m × 8 m and has a 5 m ceiling. Each person gives up about 350 kJ of heat per hour. Assuming the room is completely sealed off and insulated, calculate the air temperature rise occurring within 10 minutes. Assume C, of air 0.718 kJ/kgK and R = 0.287 kJ/kgK and each person occupies a volume of 0.05 m3.

Given data:

Number of people = 25 Room size=10m x 8m

Ceiling height = 5 m

Heat / person = 350 kJ/hr

Time, t = 10 min

C1 = 0.718 kJ/kgK

R = 0.287 kJ/kgK

=

Each person volume, V, 0.05 m3

To find:

The temperature rise of air, At

Solution:

Volume of the room, V,= 10 × 8 × 5 = 400 m3

.. Volume of air,

Va= Vr-Vpx n = 400-0.05 x 25 = 398.75 m3

Mass of air,

m = 480.35 kg

= 101.3×398.75 RT 0.287 × 293

[ ̈: Assuming, atmospheric pressure and temperature as p= 101.3 kN/m2 and T=20°C]

By first law of thermodynamics,

Q=W+AU

Assuming that heat addition is at constant volume process.

⸫ W = 0

Q = ΔU = Heat / person × Number of people

= 350 × 25 = 8750 kJ/hr

Heat loss for 10 minutes, Q = 8750 / 60 × 10 = 1458.33 kJ

Heat gained by air, Q = mCv ΔT

1458.33 = 480.35 × 0.718 × ΔT

⸫ ΔT = 4.23 °C    Ans.