Solved Anna University Problems on open systems for steady flow: Basics, Zeroth and First Law - Engineering Thermodynamics
SOLVED ANNA UNIVERSITY PROBLEMS ON OPEN SYSTEMS FOR STEADY FLOW
AU Problem 1.30
In a steady flow system, a working substance flows at a rate of 4 kg/s enters a pressure of 620 kN/m2 at a velocity of 300 m/s. The internal energy is 2100 kJ/kg and specific volume 0.37 m3/kg. It leaves the system at a pressure of 130 kN/m2, a velocity of 150 m/s, internal energy of 1500 kJ/kg and specific volume of 1.2 m3/kg. During its passage in the system, the substance has a heat transfer of loss of 30 kJ/kg to its surroundings. Determine the power of the system. State that it is from (or) to the system.
Given data:
m = 4 kg/s
p1 = 620 kN/m2
C1 = 300 m/s
u1 = 2100 kJ/kg
v1 = 0.37 m3/kg
p2 = 130 kN/m2
C2 = 150 m/s
u2 = 1500 kJ/kg
v2 = 1.2 m3/kg
Q = -30 kJ/kg
To find:
Power of the system, W
Solution:
As per SFEE,
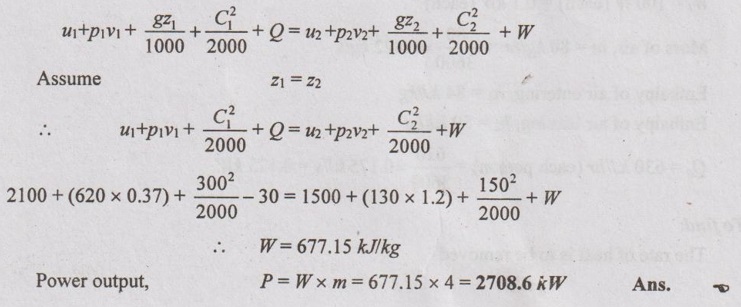
AU Problem 1.31
A working substance flows at a rate of 5 kg/s into a steady flow system at 6 bar 2000 kJ/kg internal energy and 0.4 m3/kg specific volume with a velocity of 300 m/s. It leaves at 10 bar, 1600 kJ/kg of internal energy, 1.2 m3/kg of specific volume with a velocity of 150 m/s. The inlet is 10 m above the outlet. The work transfer to the surroundings is 3 MW. Evaluate the change in enthalpy and estimate the heat transfer and indicate the direction.
Similar to AU Problem 1.30 on Page 1.149.
[Ans:- Δh = -560 kJ/kg, Q = 5630 kJ/s, Q is gained by the system]
[Note: Change in enthalpy, Δh = h1 - h2 = (u + p1v1) - (u2 + p2v2)
= (2000 + 600 × 0.4) - (1600 + 1000 × 1.2) = -560 kJ/kg]
AU Problem 1.32
A room for four persons has two fans, each consuming 0.18 kW power and three 100 W lamps. Ventilation air at the rate of 80 kg/hr enters with an enthalpy of 84 kJ/kg and leaves with an enthalpy of 59 kJ/kg. If each person puts out heat at the rate of 630 kJ/hr, determine the rate at which heat is to be removed by a room cooler so that a steady state is maintained in the room.
Given data:
np = 4 (persons)
nf = 2 (fans)
n1 = 3 (lamps)
Wf = 0.18 kW (each)
W1 = 100 W (each) = 0.1 kW (each)
Mass of air, m = 80 kg/hr = 80 / 3600 = 0.022 kg/s
Enthalpy of air entering, h1 = 84 kJ/kg
Enthalpy of air leaving, h2 = 59 kJ/kg
Qp = 630 kJ/hr (each person) = 630 / 3600 = 0.175 kJ/s = 0.175 kW
To find:
The rate of heat is to be removed
Solution:
Rate of energy increase = Rate of energy inflow - Rate of energy outflow
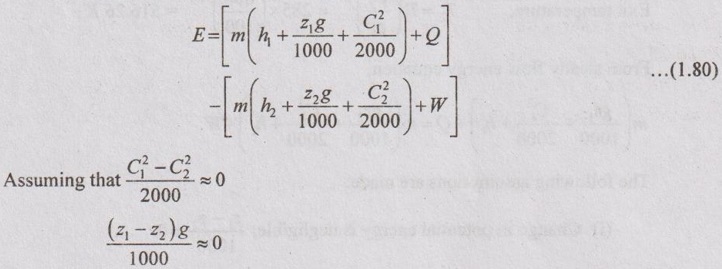
Now, the equation (1.80) reduces to
E = mh1 + Q - mh2 – W = m(h1 – h2)+ Q - W
Q = E - m(h1 – h2)+ W
E = -npQp = -4 × 0.175 = -0.7 kW
m(h1 – h2) = 0.022 (84 - 59) = 0.55 kW
W = Electrical energy consumption or work input
= −nfWf - nlWl = -2 × 0.18 – 3 × 0.1 = -0.66 kW
⸫ Q = -0.7 - 0.55 - 0.66 = -1.91 kW Ans.
AU Problem 1.33
Air is compressed by an adiabatic compressor from 100 kPa and 12 °C to a pressure of 800 kPa at a steady rate of 0.2 kg/s. If the isentropic efficiency of the compressor is 80%, determine the exit temperature of air and the required power input to the compressor.
Given data:
Process: Adiabatic compression
At inlet, p1 = 100 kPa = 100 kN/m2
T1 = 12°C = 12 + 273 = 285 K
At outlet, p2 = 800 kPa = 800 kN/m2
m = 0.2 kg/s
ηc = 80%
Solution:

Therefore, the above equation reduces to
mh1 = mh2 + W
W = mh2 - mh1
W = m(h2 – h1)
W = mCp (T2 – T1)
= 0.2 × 1.005(516.26 - 285) = 46.48 kW
Actual work supplied to the compressor will be more than the ideal work.
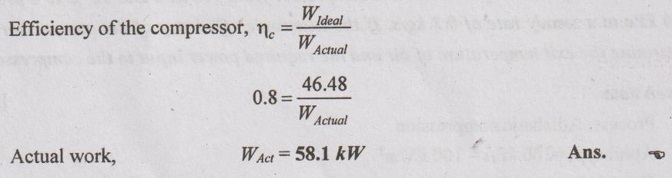
AU Problem 1.34
Air flows steadily at the rate of 0.5 kg/s through an air compressor, entering at 7 m/s velocity, 100 kPa pressure and 0.95 m3/kg, volume and leaving at 5m/s, 700 kPa and 0.19 m3/kg. The internal energy of the air leaving is 90 kJ/kg greater than air entering. Cooling water in the compressor jackets absorbs heat from the air at the rate of 58 kW. (a) Compute the rate of shaft work input to the air in kW. (b) Find the ratio of the inlet pipe diameter to the outlet pipe diameter.
Same as Problem 1.34 on Page 1.146.
AU Problem 1.35
A gas flows steadily through a compressor. The gas enters the compressor at a temperature of 60° C, a pressure of 100 kPa and an enthalpy of 391.2 kJ/kg. The gas leaves the compressor at a temperature of 245°C, a pressure of 0.6 MPa and an enthalpy of 534.5 kJ/kg. There is no heat transfer to or from the gas as it flows through the compressor. Evaluate the external work done per unit mass of gas when the velocity at entry 80 m/s and that at exit is 160 m/s.
Given data:
T1 = 60°C = 60 + 273 = 333 K
p1 = 100 kPa
h1 = 391.2 kJ/kg
T2 = 245°C = 245 + 273 = 518 K
p1 = 0.6 MPa
h2 = 534.5 kJ/kg
Q = 0
C1 = 80 m/s
C2 = 160 m/s
To find:
External work done per unit mass of gas
Solution:
As per SFEE,
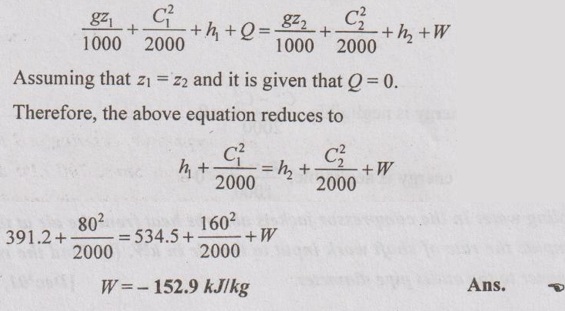
AU Problem 1.36
Air is compressed from 100 kPa and 22° C to a pressure of 1 MPa while being cooled at the rate of 16 kJ/kg by circulating water through the compressor casing. The volume flow rate of air at inlet condition is 150 m3/min and power input to compressor is 500 kW. Neglecting the gravitational potential energy, determine the mass flow rate and the temperature of air at exit.
Same as Problem 1.35 on Page 1.147.
AU Problem 1.37
A reciprocating air compressor takes in 2 m3/min air at 0.11 MPa, 298 K which delivers at 1.5 MPa, 384 K to an after cooler where the air is cooled at constant pressure to 298 K. The power absorbed by the compressor is 4.15 kW. Determine the heat transfer in (i) the compressor (ii) the cooler. State your assumptions.
Given data:
v1 = 2 m3/min = 2/60 = 0.033 m3/s
p1 = 0.11 MPa = 110 kN/m2
T1 = 298 K
p2 = 1.5 MPa = 1500 kN/m2
T2 = 384 K
T3 = 298 K
W = -4.15 kW
Solution:
Assumptions:
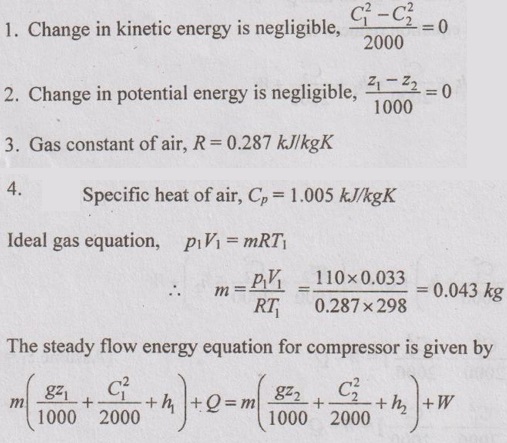
Q = W + m (h2 - h1)
= W + m Cp(T2 - T1)
Q = -4.15 + 0.043 × 1.005 × (384 - 298)
= -0.434 kW Ans. 
The cooler cools the air at constant pressure. Therefore,
Q = m Cp(T3 – T2)
Q = 0.043 × 1.005 × (298 - 384) = -3.72 kW Ans. 
AU Problem 1.38
Air enters the compressor of a gas-turbine plant at ambient conditions of 100 kPa and 25°C with a low velocity and exits at 1 MPa and 347°C with a velocity of 90 m/s. The compressor is cooled at a rate of 1500 kJ/min and the power input to the compressor is 250 kW. Determine the mass flow rate of air through the compressor. Assume Cp 1.005 kJ/kgK.
Given data:
p1 = 100 kPa
T1 = 25°C = 25 + 273 = 298 K
C1 = 0
p2 = 1 MPa = 1000 kPa
T2 = 347°C = 347 + 273 = 620 K
C2 = 90 m/s
Q = -1500 kJ/min = -25 kW
W = -250 kW
Cp = 1.005 kJ/kgK
Solution:
SFEE is given by
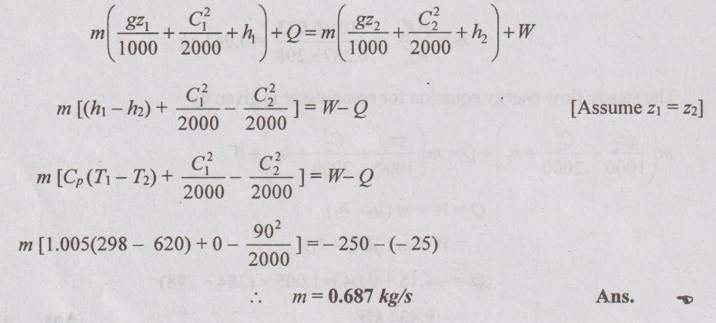
AU Problem 1.39
A turbine operates under steady flow conditions receiving steam at the following state: pressure = 1.2 MPa, temperature = 188°C, enthalpy = 2785 kJ/kg, velocity= 33.3 m/s and elevation = 3 m. The steam leaves the turbine at the following state: pressure = 20 kPa, enthalpy = 2512 kJ/kg, velocity = 100 m/s and elevation = 0 m. Heat is lost to the surroundings at the rate of 0.29 kJ/s. If the rate of steam flow through the turbine is 0.42 kg/s, what is the power output of the turbine in kW?
Same as Problem 1.32 on Page 1.144.
AU Problem 1.40
In a gas turbine installation, the gases enter the turbine at the rate of 5 kg/s with a velocity of 50 m/s and enthalpy of 900 kJ/kg and leave the turbine with 150 m/s and enthalpy of 400 kJ/kg. The loss of heat from the gases to the surroundings is 25 kJ/kg. Assume R = 0.285 kJ/kgK, Cp = 1.004 kJ/kgK and inlet conditions to be at 100 kPa and 27°C. Determine the work done and diameter of the inlet pipe.
Given data:
m = 5 kg/s
C1 = 50 m/s
h1 = 900 kJ/kg
C2 = 150 m/s
h2 = 400 kJ/kg
Q = -25 kJ/kg = -25 kJ/kg × 5 kg/s = 125 kJ/s = - 125 kW
R = 0.285 kJ/kgK
Cp = 1.004 kJ/kgK
p1 = 100 kPa
T1 = 27°C = 27 + 273 = 300 K
Solution:
From SFEE,
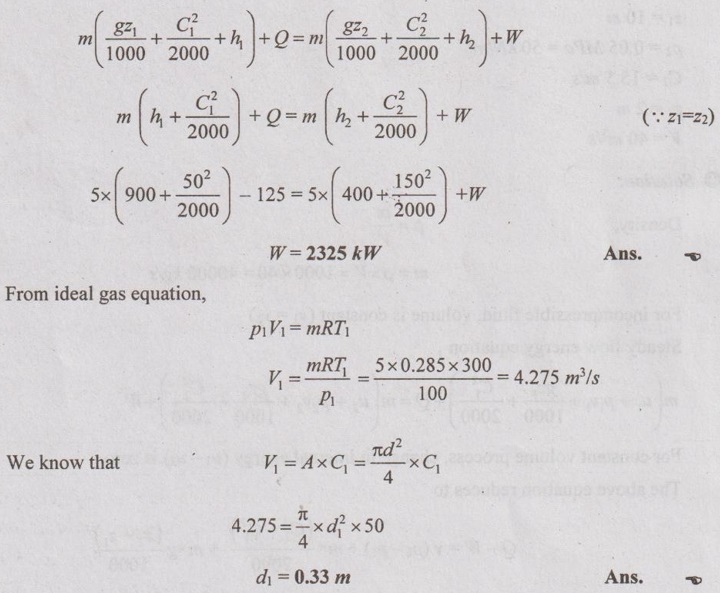
AU Problem 1.41
In a turbo machine handling an incompressible fluid with a density of 1000 kg/m3 the conditions of the fluid at the rotor entry and exit are as given below:

If the volume flow rate of the fluid is 40 m3/s, estimate the net energy transfer from the fluid as work.
Given data:
ρ = 1000 kg/m3
p1 = 1.15 MPa = 1150 kN/m2
C1 = 30 m/s
z1 = 10 m
p2 = 0.05 MPa = 50 kN/m2
C2 = 15.5 m/s
z2 = 2 m
V = 40 m3/s
Solution:

AU Problem 1.42
The air speed of a turbo jet engine in flight is 270 m/s. Ambient Air temperature is 15°C. Gas temperature at the outlet of the nozzle is 600°C. Corresponding enthalpy values for air and gas are 260 and 912 kJ/kg respectively. Fuel-air ratio is 0.019. Chemical energy in the fuel is 44.5 MJ/kg. Owing to incomplete combustion 5% of the chemical energy is not released in the reaction. Heat loss from the engine is 21 kJ/kg of air.
i) Draw the schematic diagram and indicate all the mass and energy interactions taking jet engine as a system.
ii) Calculate the velocity of the exhaust jet,
iii) Also calculate the thrust per unit mass flow rate of air, given that the thrust is the forward force on jet engine due to rate of change of momentum of working fluid.
Given data:
Air speed of turbojet engine, Ca = 270 m/s
Ambient air temperature = -15°C
Gas temperature at outlet of nozzle = 600°C
Enthalpy of air, ha = 260 kJ/kg
Enthalpy of gas, hg = 912 kJ/kg
Fuel air ratio = 0.019
Chemical energy of the fuel = 44.5 MJ/kg = 44500 kJ/kg
Heat loss from the engine, Q = 21 kJ/kg of air
Solution:
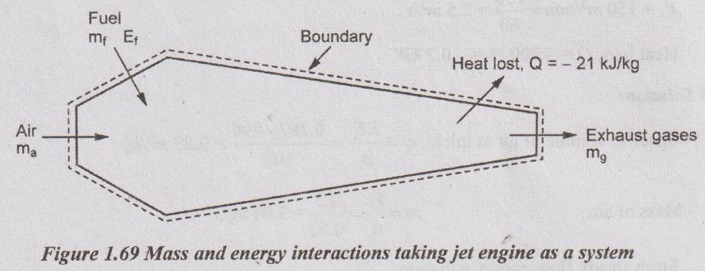
It is given that fuel air ratio = 0.019, i.e., mass of air, ma = 1 kg, then mass of fuel, mf = 0.019 kg and hence mass of gas, mg = 1 + 0.019 = 1.019 kg.
Applying SFEE to this turbo jet engine system,
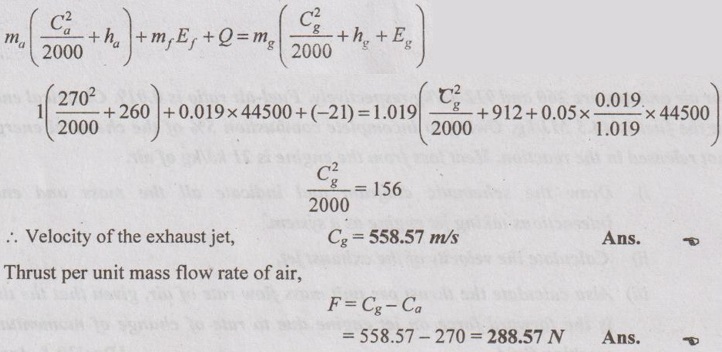
AU Problem 1.43
The electric heating system used in many houses consists of a simple duct with resistance wire. Air is heated as it flows over resistance wires. Consider a 15 kW electric heating system. Air enters the heating section at 100 kPa and 17°C with a volume flow rate of 150 m3/min. If heat is lost from the air in the duct to the surroundings at a rate of 200 W, determine the exit temperature of air.
Given data:
Work input, W = -15 kW
At inlet, p1 =100 kPa = 100 kN/m2
T1 = 17°C = 273 + 17 = 290 K
V1 = 150 m3/min = 150/60 = 2.5 m3/s
Heat loss, Q = -200 W = -0.2 kW
Solution:
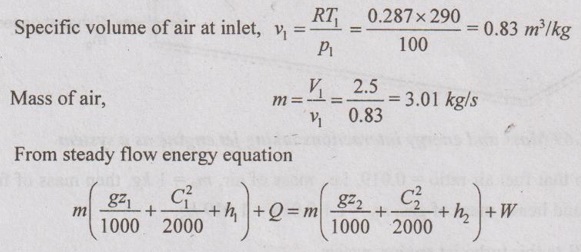
The following assumptions are made:
AU Problem 1.44
A certain water heater operates under steady flow conditions receiving 4.2 kg/s of water at 75°C temperature, enthalpy 313.93 kJ/kg. The water is heated by mixing with steam which is supplied to the heater at temperature 100.2°C and enthalpy 2676 kJ/kg. The mixture leaves the heater as liquid water at temperature 100°C and enthalpy 419 kJ/kg. How much steam must be supplied to the heater per hour?
Given data:
m1 = 4.2 kg/s
T1 = 75°C = 75 + 273 = 348 K
h1 = 313.93 kJ/kg
T2 = 100.2°C = 100.2 + 273 = 373.2 K
h2 = 2676 kJ/kg
T3 = 100°C = 100 + 273 = 373 K
h3 = 419 kJ/kg
To find:
m2
Solution:
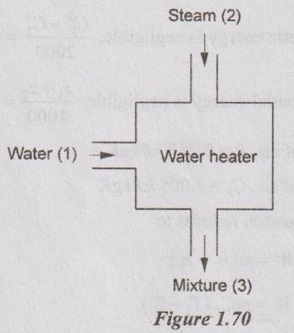
By mass balance,
Sum of masses entering the heater = Sum of masses leaving the heater
m1 + m2 = m3
Similarly, energy balance at the heater,
Sum of energies entering the heater = Sum of energies leaving the heater
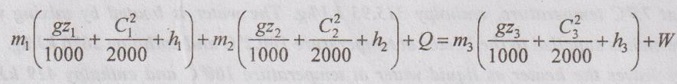
The following assumptions are made:
(i) There is no shaft work (W = 0).
(ii) There is no change in datum. So, the change in potential energy is neglected.
(iii) Kinetic energy is also neglected.
(iv) The heater is assumed to be well-insulated (Q = 0).
So, the above energy reduces to
m1h1 + m2h2 = m3h3
Again it can be written as
m1h1 + m2h2 = (m1 + m2) h3
4.2 × 313.93 + m2 × 2676 = (4.2 + m2) × 419
1318.5 + 2676 m2 = 1759.8 + 419m2
m2 = 0.196 kg/s = 705.6 kg/hr Ans.
AU Problem 1.45
In an isentropic flow through nozzle, air flows at the rate of 600 kg/hr. At inlet to the nozzle, pressure is 2 MPa and temperature is 127° C. The exit pressure is 0.5 MPa. Initial air velocity is 300 m/s. Determine the (i) exit velocity of air and (ii) inlet and exit area of nozzle.
Given data:
Mass flow rate, m = 600 kg/hr = 600 / 3600 = 0.167 kg/s
Pressure at inlet, p1 = 2 MPa = 2000 kN/m2
Temperature at inlet, T1 = 127°C = 127 + 273 = 400 K
Pressure at inlet, p2 = 0.5 MPa = 500 kN/m2
Velocity at inlet, C1 = 300 m/s
Solution:
From the isentropic relation,
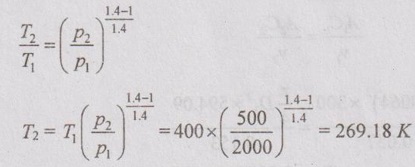
The steady flow energy equation for a nozzle is given by
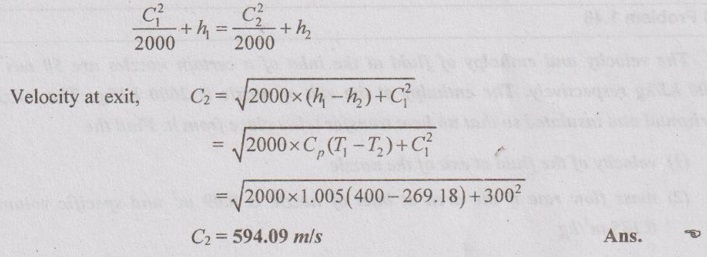
From ideal gas equation,
p1v1 = RT1
2000 × v1 = 0.287 × 400
⸫ v1 = 0.057 m3/kg

We know that for isentropic process,
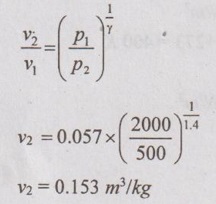
By conservation of mass,
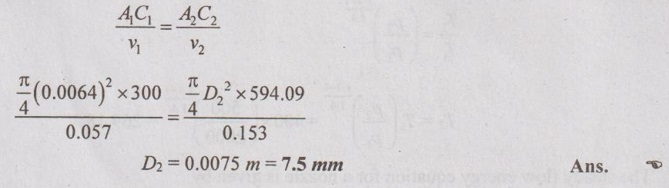
AU Problem 1.46
The velocity and enthalpy of fluid at the inlet of a certain nozzles are 50 m/s and 2800 kJ/kg respectively. The enthalpy at the exit of nozzle is 2600 kJ/kg. The nozzle is horizontal and insulated so that no heat transfer takes place from it. Find the
(1) velocity of the fluid at exit of the nozzle
(2) mass flow rate if the area at inlet of nozzle is 0.09 m2 and specific volume is 0.185 m3/kg
(3) exit area of the nozzles if the specific volume at the exit of the nozzle is 0.495 m3/kg.
Given data:
C1 = 50 m/s
h1 = 2800 kJ/kg
h2 = 2600 kJ/kg
A1 = 0.09 m2
v1 = 0.185 m3/kg
v2 = 0.495 m3/kg
Q = 0
z1 = z2
Solution:
SFEE for nozzle is given by
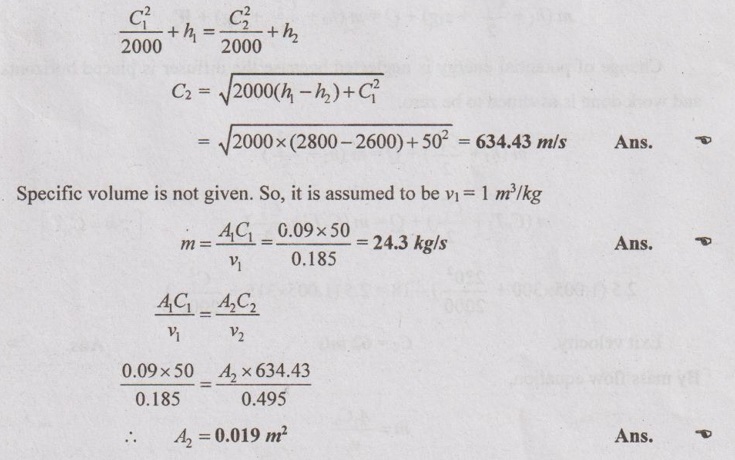
AU Problem 1.47
Air at 80 kPa, 27°C and 220 m/s enters a diffuser at a rate of 2.5 kg/s and leaves at 42°C. The exit area of the diffuser is 400 cm2. The air is estimated to lose heat at a rate of 18 kJ/s during this process. Determine the:
(i) exit velocity and
(ii) exit pressure of the air.
Given data:
p1 = 80 kPa
T1 = 27°C = 273 + 27 = 300 K
C1 = 220 m/s
m = 2.5 kg/s
T2 = 42°C = 273 + 42 = 315 K
A2 = 400 cm2 = 0.04 m2
Q = -18 kJ/s
Solution:
By SFEE,
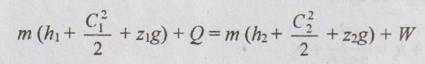
Change of potential energy is neglected because the diffuser is placed horizontally and work done is assumed to be zero.
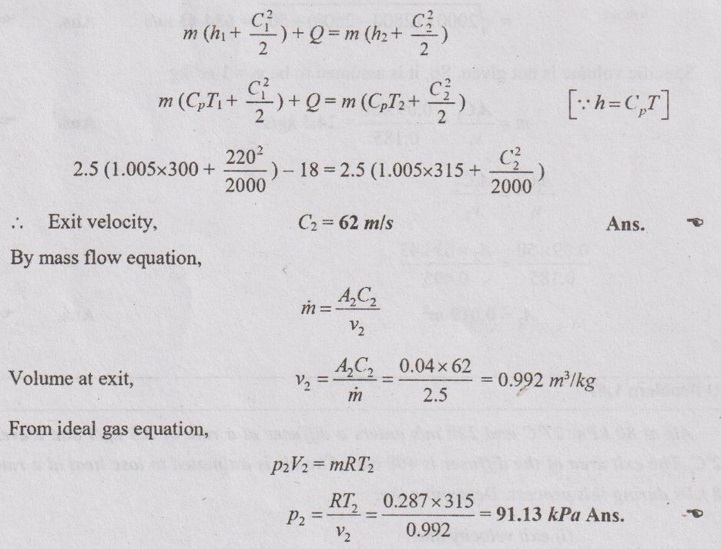
AU Problem 1.48
A centrifugal pump delivers 2750 kg of water per minute from initial pressure of 0.8 bar absolute to a final pressure of 2.8 bar absolute. The suction is 2 m below and the delivery is 5 m above the center of pump. If the suction and delivery pipes are of 15 cm and 10 cm diameter respectively, make calculation for power required to run the pump.
Given data:
m = 2750 kg/min = 2750 / 60 = 45.83 kg/s
p1 = 0.8 bar = 80 kN/m2
p2 = 2.8 bar = 280 kN/m2
z1 = -2 m
z2 = 5 m
d1 = 15 cm = 0.15 m
d2 = 10 cm = 0.1 m
p = 1000 kg/m3 for water
⸫ v1 = v2 = v = 0.001 m3/kg
Solution:
We know that
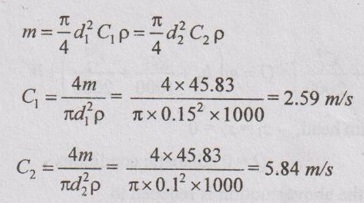
The steady flow energy equation is given by

AU Problem 1.49
A blower handles 1 kg/s of air at 293 K and consumes a power of 15 kW. The inlet and outlet velocities of air are 100 m/s and 150 m/s respectively. Find the exit air temperature, assuming adiabatic conditions. Take C, of air as 1.005 kJ/kgK.
Given data:
m =1 kg/s
T1 = 293 K
W = -15 kW
C1 = 100 m/s
C2 = 150 m/s
Cp = 1.005 kJ/kgK
Solution:

AU Problem 1.50
Air at a temperature of 15°C passes through a heat exchanger at a velocity of 30 m/s where its temperature is raised to 800°C. It then enters a turbine with the same velocity of 30 m/s and expands until the temperature falls to 650°C. On leaving the turbine, the air is taken at a velocity of 60 m/s to a nozzle where it expands until the temperature has fallen to 500°C. If the air flow rate is 2 kg/s, calculate the
(i) rate of heat transfer to the air in the heat exchanger,
(ii) power output from the turbine assuming no heat loss, and
(iii) velocity at exit from the nozzle, assuming no heat loss.
Take the enthalpy of air as h=CpT, where Cp is the specific heat equal to 1.005 kJ/kgK and 'T' the temperature.
Given data:
T1 = 15°C = 15 + 273 = 288 K
C1 = 30 m/s
T2 = 800°C = 800 + 273 = 1073 K
C2 = 30 m/s
T3 = 650°C = 650 + 273 = 923 K
C3 = 60 m/s
T4 = 500°C = 500 + 273 = 773 K
m = 2 kg/s
To find:
Q1-2, W2-3 and C4
Solution:
SFEE between 1-2 (Heat exchanger),
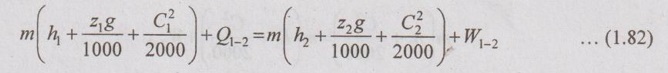
For heat exchanger, the following assumptions can be applied:
(i) There is no work transfer (W1-2 = 0).
(ii) There is no change in datum (z1 = z2).
(iii) Kinetic energy is also neglected (C1 = C2).
So, the above equation reduces to
Q1-2 = m(h2 – h1)
= mCp (T2 – T1)
= 2 × 1.005 × (1073 - 288)
= 1577.85 kW Ans.
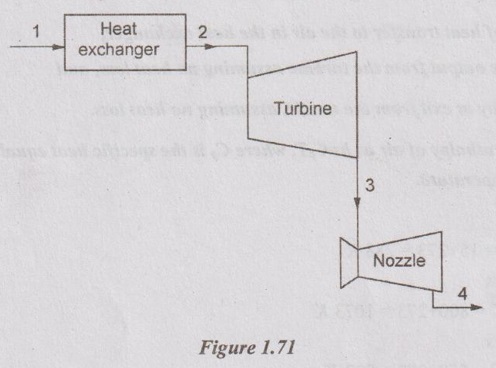
Applying SFEE between 2-3 (Turbine)
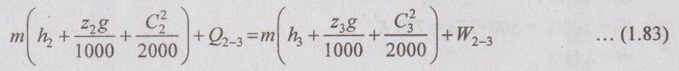
For turbine, the following assumptions can be applied:
(i) There is no heat transfer (Q2-3 = 0).
(ii) There is no change in datum (z2 = z3).
⸫ Equation (1.83) reduces to
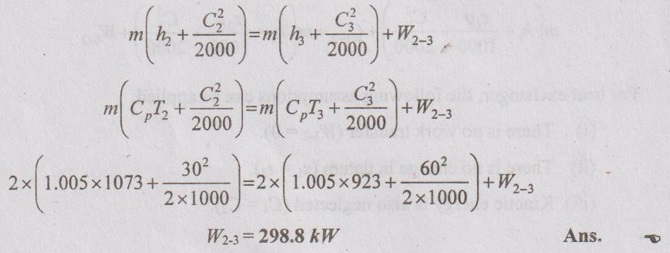
Similarly, applying SFEE between 3-4 (Nozzle),
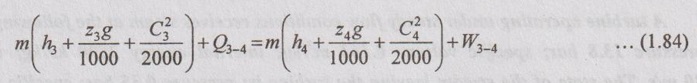
For nozzle, the following assumptions can be applied:
(i) There is no work transfer (W3-4 = 0).
(ii) There is no change in datum (z3 = z4).
It is also given that there is no heat loss occurs in the nozzle (Q3-4 = 0).
⸫ Equation (1.84) reduces to
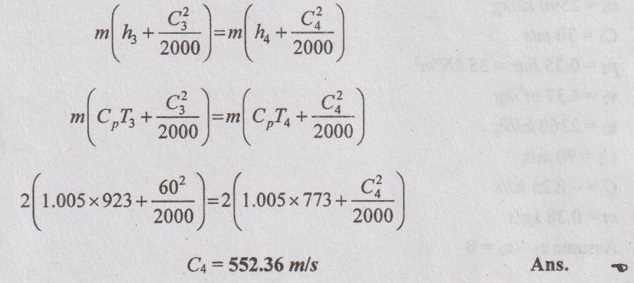
AU Problem 1.51
In a gas turbine installation air is heated inside heat exchanger up to 750°C from ambient temperature of 27°C. Hot air then enters into gas turbine with the velocity of 50 m/s and leaves at 600°C. Air leaving the turbine enters a nozzle at 60 m/s velocity and leaves nozzle at temperature of 500°C. For unit mass flow rate of air, determine the following assumptions adiabatic expansion in turbine and nozzle,
(i) heat transfer to air in heat exchanger
(ii) power output from turbine
(iii) velocity at exit of nozzle. Take Cp for air as 1.005 kJ/kgK.
Similar to AU Problem 1.50 on Page 1.169.
[Ans:- Q1-2 = 726.615 kW, W2-3 = 150.2 kW and C4 = 452.33 m/s]
AU Problem 1.52
A turbine operating under steady flow conditions receives steam at the following state: pressure 13.8 bar; specific volume 0.143 m3/kg; internal energy 2590 kJ/kg; velocity 30 m/s. The state of the stream leaving the turbine is: pressure 0.35 bar; specific volume 4.37 m3/kg: internal energy 2360 kJ/kg: velocity 90 m/s. Heat is lost to the surroundings at the rate of 0.25 kJ/s. If the rate of steam flow is 0.38 kg/s, what is the power developed by the turbine?
Given data:
p1 = 13.8 bar = 1380 kN/m2
v1 = 0.143 m3/kg
u1 = 2590 kJ/kg
C1 = 30 m/s
p2 = 0.35 bar = 35 kN/m2
v2 = 4.37 m3/kg
u2 = 2360 kJ/kg
C2 = 90 m/s
Q = -0.25 kJ/s
m = 0.38 kg/s
Assume z1 - z2 = 0
Solution:
By SFEE,
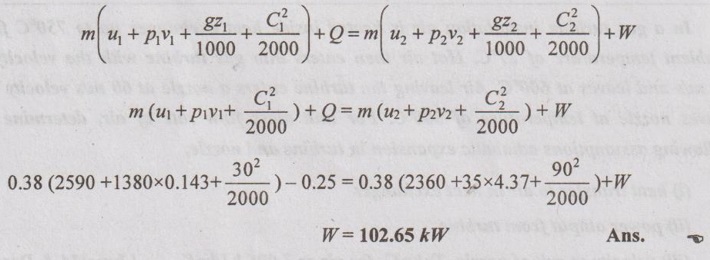
No comments:
Post a Comment