Concept of Continuum

 A continuous homogenous medium is called continuum. Continuum is based on the macroscopic approach.

CONCEPT OF CONTINUUM

A continuous homogenous medium is called continuum. Continuum is based on the macroscopic approach. The continuum idealization allows us to treat the properties as point functions and assumes the properties varying continually in space with no jump discontinuities. This idealization is valid as long as the size of the system is large relative to the space between molecules. From the macroscopic perspective, the description of matter is simplified by considering it to be distributed continuously throughout a region. Here, the matter is treated as continuous one instead of disregarding the behaviour of individual molecules.

For example, consider the mass δm with a volume of δV surrounding the point 'P' as Sm shown in Figure 1.8. Within the volume δV, the average mass density of the system is δm / δV. When the substances can be treated as continuous, it is possible to speak of their intensive thermodynamic properties "at a point." Hence, δV becomes very small at that particular point Sm 'P'. If the graph is plotted between δm / δV and δV, the average mass density tends to approach equal value as δV increases. If δV becomes very small, relatively few molecules will pass into and out of the control volume in a random motion. Therefore, the average density varies with time. It is very difficult to determine a definite value of δm / δV. When the smallest volume of δV1 is continuous, the density ρ of the system at any particular point 'P' is defined as

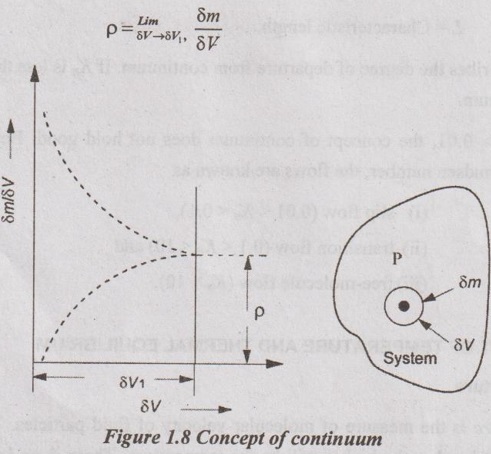
At the same time, the fluid velocity at 'P' is instantaneous velocity of the center of gravity of the smallest corresponding continuous volume δV1. The volume δV1 contains enough particles for statistical average to be significant. It is the smallest volume for which the matter can be considered a continuum and it is normally small enough that it can be considered as a "point." The density or local mass per unit volume is an intensive property that may vary from point to point within a system.

Note:

The concept of continuum is valid when the mean path of molecules approaches the magnitude of the vessel dimensions as well as macroscopic approach.

1. Kundsen Number in Continuum

A continuous homogenous medium is called continuum. Continuum is based on the macroscopic approach. The continuum idealization allows us to treat the properties as point functions and assumes the properties varying continually in space with no jump discontinuities. This idealization is valid as long as the size of the system is large relative to the space between molecules.

A dimensionless parameter known as Knudsen number is given by

Kn = λ / L

where λ = Mean free path and

L = Characteristic length.

It describes the degree of departure from continuum. If Kn is less than 0.01, the fluid is a continuum.

If Kn > 0.01, the concept of continuum does not hold good. Beyond this critical range of Knudsen number, the flows are known as

(i) slip flow (0.01 < Kn < 0.1),

(ii) transition flow (0.1 < Kn < 10) and

(iii) free-molecule flow (Kn > 10).