Work Transfer (W)

 Work is an energy interaction between a system and its surroundings.

WORK TRANSFER (W)

Work is an energy interaction between a system and its surroundings. Usually, the energy can cross the boundary of any system in the form of either heat or work. But, the energy crossed through the boundary in a closed system is definitely in the form of work.

As with the heat, the amount of work done by or on a system depends upon the path and not simply on the initial and final conditions of the system.

Work is defined as the product of force and distance moved in the direction of the force applied. Specifically, it is the energy transfer associated with force acting through a distance.

Work = Force × Distance moved

W = F × x             ... (1.5)

The work is expressed in terms of N-m or J

The work done per unit time is called power. The unit of power is kJ/s or kW.

When a boundary of a closed system moves in the direction of the force acting on it, then the surroundings do work on the system. When the boundary moves outwards, the work is done by the system on its surroundings. Work done by the system is taken as positive work and work done on the system is taken as negative work.

In other words, it can be stated that the work output from any system is taken as positive work.

Example: Heat engine, turbines, etc.

The work supplied to the system is taken as negative work. 

Example: Compressor, fans, heat pump, etc.

Work is a form of energy but it is energy in transit. Work is not a property of a system. Work is a process done by or on a system but a system contains no work. Heat and work are both transitory energies and they must not be confused with internal energy possessed by a system. For example, when a gas contained in a rigid container is heated, both pressure and temperature of the gas increase and hence, the internal energy of the gas will also increase. The increase in internal energy has been caused by the heat flow to the system.

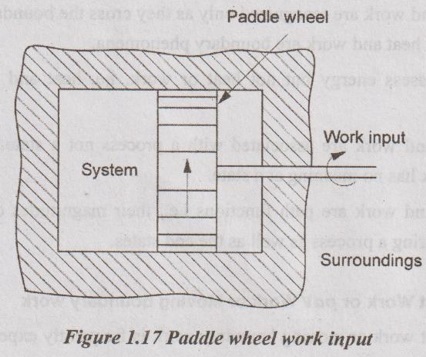
Another way in which the work may be transferred to a system is illustrated in Figure 1.17. The paddle wheel imparts a change in momentum to the fluid and a work input is required to turn the shaft. The kinetic energy attained by the fluid is dissipated by internal fluid friction and friction between fluid and a container. When the container is insulated, the whole work input helps to increase the internal energy of the system.

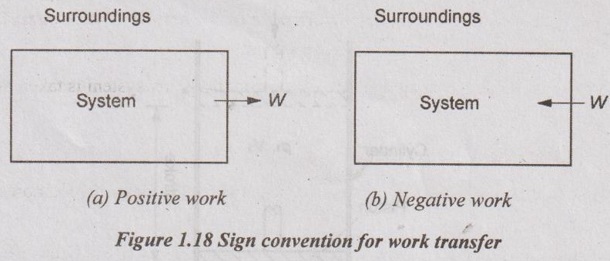
Sign conventions:

(i) If the work is done by the system, W is positive work (refer Figure 1.18(a)) 

(ii) If the work is done on the system, W is negative work (refer Figure 1.18(b)).

1. Comparison of Work and Heat Transfers

From above discussion on heat transfer and work transfer, both heat and work are energy transfer mechanisms between a system and its surroundings. The similarities between them exist as follows:

(a) Both heat and work are recognized only as they cross the boundaries of a system. It means, both heat and work are boundary phenomena.

(b) Systems possess energy but not heat or work. i.e. heat and work are transient phenomena.

(c) Both heat and work are associated with a process not a state. Unlike properties, heat or work has no meaning at a state.

(d) Both heat and work are path functions i.e., their magnitudes depend on the path followed during a process as well as the end states.

2. Displacement Work or pdV Work or Moving boundary work

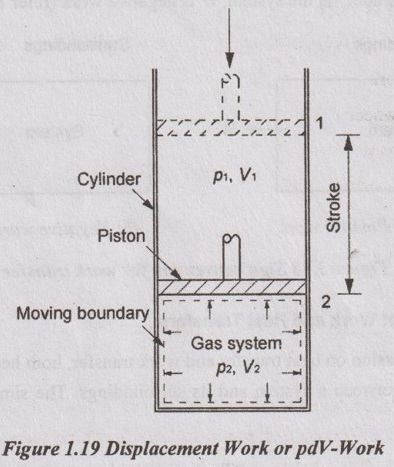
The displacement work or moving boundary work is frequently experienced in practice. It is associated with either compression or expansion of a gas in a piston-cylinder device. The work is performed by the movement of boundary due to the fluid pressure acting on the piston.

Consider a gas sealed in a container with a tightly fitting yet movable piston as shown in Figure 1.19. The system is in thermal equilibrium at state 1. Let p1 and V1 be the initial pressure and temperature of the gas respectively. Let the piston moves from state 1 to a new state 2. The system is also in thermodynamic equilibrium at state 2. The pressure and volume at this state 2 are given by p2 and V2 respectively.

We know that

Pressure on the piston,

p = Force acting on piston (F) / Area of the piston (A)

⸫ Force acting on the piston, F = p × A

When the piston is moved an infinitesimal distance (ds), infinitesimal work (dW) is done on the piston to compress the gas. Mathematically, it is given

dW = F × ds = pAds = pdV [⸪ Volume, V = Area (A) × distance (s)]

When the piston moves from position 1 to position 2, the volume is decreased from V1 to V2. During the process, the amount of work done on the system is given as follows:

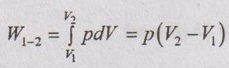
3. Other Modes of Work

In addition to displacement work, many other forms of work are involved during the energy transfer between system and surroundings. They are:

1. Mechanical work

2. Non-mechanical work.

(a) Mechanical forms of work

The mechanical work is again categorized into the following forms.

1. Shaft work

2. Paddle wheel work

3. Spring work

4. Elastic solid bar work

5. Gravitational work

6. Acceleration work

7. Flow work

8. Work associated with stretching of a liquid film.

1. Shaft work:

Shaft is a rotating machine element which transmits power from one member to another member. It is one of the most common and basic machine elements which are used in mechanical equipment. It is used with power transmission elements such as gears, pulleys, flywheels, cranks, etc. These shafts are designed to transmit the required torque and to support the rotating elements such as gears and pulleys.

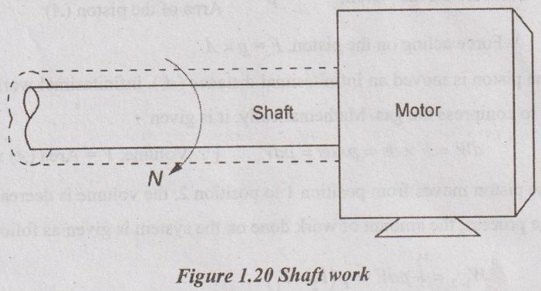
The torque T applied to the shaft is constant which indicates the force F applied also constant. We know that the torque acting on the shaft,

T = F × r       ... (1.6)

where

F = Force applied on the shaft in N (Newton)

r = Radius of the shaft in m.

The unit of torque is N-m.

So, force,

F = T / r                      ... (1.7)

But the torque can be calculated using its dimensions (size) and shear stress of the shaft material.

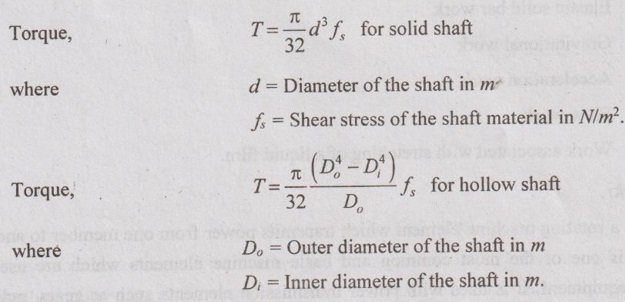
We know that the mechanical work is the product of force applied, F and the distance moved, s in the direction of force applied. The distance moved, s = (πd) for one revolution of the shaft. The unit of distance is in m (metre).

The total distance covered by the shaft is given by

s = (πd) N for 'N' revolutions

For a particular constant torque, the work done in kJ for 'N' revolutions can be calculated by

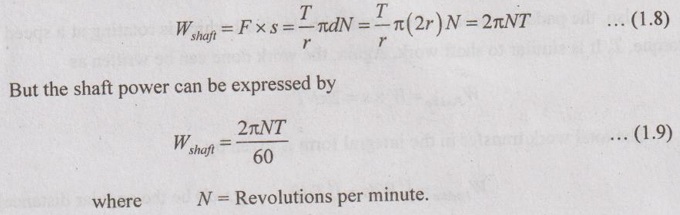
2. Paddle wheel work:

The rotating wheel called paddle wheel is connected at one end of the connecting member and the other end is connected with the rotating drum which has the rope with a weight as shown in Figure 1.21.

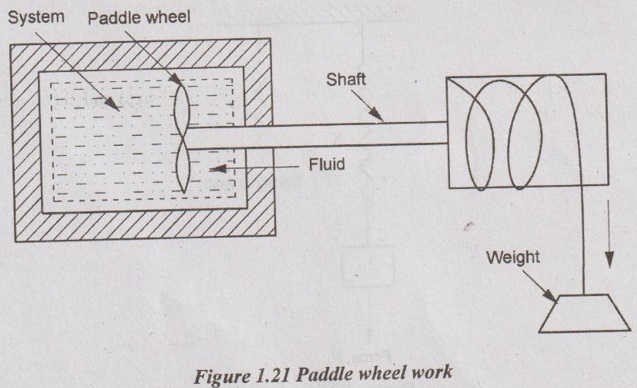
The paddle is kept inside the fluid cylinder. When the weight is lowered from its initial position, the paddle wheel rotates by stirring the fluid in the cylinder. Since this cylinder is rigid with constant volume, there is no work on or by the fluid. So, the work is done on the fluid. It is given by

But, the weight 'W' is lowered through a distance 's'.

Therefore, the paddle wheel work done on the system can be expressed by

WPaddle = W × s               ..... (1.11)

Also, the paddle wheel is connected with the shaft which is rotating at a speed of N with torque, T. It is similar to shaft work. Again, the work done can be written as

WPaddle = W × s = 2πNT     ... (1.12)

The total work transfer in the integral form is given by

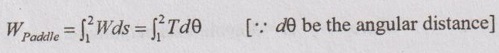
3. Spring work:

Spring is an elastic member which deflects under the action of load and regains its original shape after the load is removed. Springs are quite commonly used in automobiles, railway wagons, valves, watches etc.

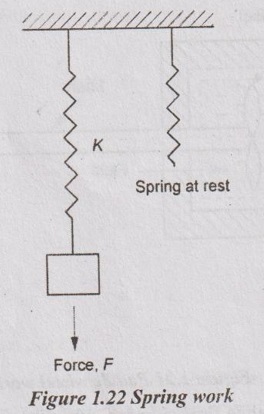
When the force is applied on a spring, the spring length changes. The elongation of the spring is dx distance for the applied force F. The spring work can be calculated by

Wspring = F × x

So, the total spring can be expressed by

We know that the force of spring is given by

F = K × x             ... (1.14)

where

K = Spring constant or spring stiffness in N/m or kN/m

Substituting the equation (1.14) in equation (1.13),

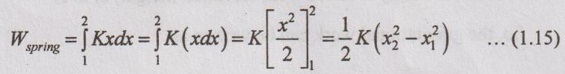
where x1 and x2 are the initial and final displacements of the spring while applying the force, F.

4. Work done on elastic solid bar:

Solid bars are similar to linear springs because it may contract or elongate under the action of applied force. The nature of elastic bodies is that when the force is withdrawn, they return to their original length similar to a spring. Therefore, the equations given for a linear spring can also be used for elastic solid bars.

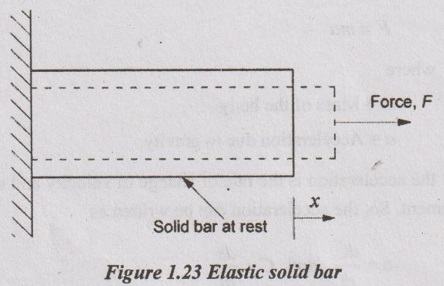
Alternately, the work associated with the expansion or contraction of an elastic solid bar can be calculated by replacing pressure p in N/m2 and area A in m2 of its counterpart in solids.

5. Gravitational work:

If the work is done by or against the gravitational force field, it is called gravitational work. It is indirectly performed at the expense of potential energy. So, the potential energy of the body increases when a body is raised in a gravitational field. Therefore, the work transfer needed to raise a body is equal to the change in the potential energy of the body, So, the force acting on the body having the mass, m is given by

F = mg      ..... (1.17)

where

g = Acceleration due to gravity in m/s2

Assume, the body is raised from elevation (height) z1 to z2

So, the gravitational work can be written as

6. Acceleration work:

When a body is accelerated, its kinetic energy increases. The acceleration work is mainly used in elevators, escalators, conveyor belts and ski-lifts. It also plays a primary role in the design of automotive and aircraft engines. The work transfer needed to accelerate a body is equal to the change in the kinetic energy of the body.

By Newton's second law

F = ma              ...(1.19)

where

m = Mass of the body

a = Acceleration due to gravity.

We know that the acceleration is the rate of change of velocity and velocity is the rate of change on displacement. So, the acceleration can be written as

where

C = Velocity of the body

t = Time for the distance travelled

s = Displacement of the body.

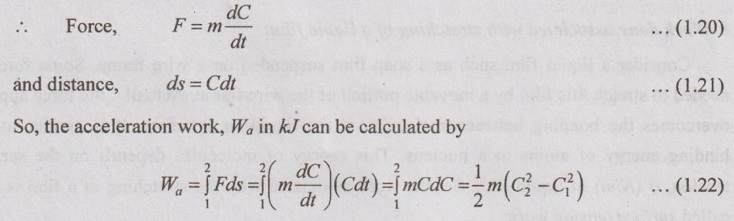
7. Flow work:

Flow work is only possible in open systems under flow process. It is the work transfer across the boundary of the system. For example, the energy transfer in compressor, blower, turbine etc. The force acting on the fluid is associated with fluid pressure, p and contact area, A of the moving body with the fluid.

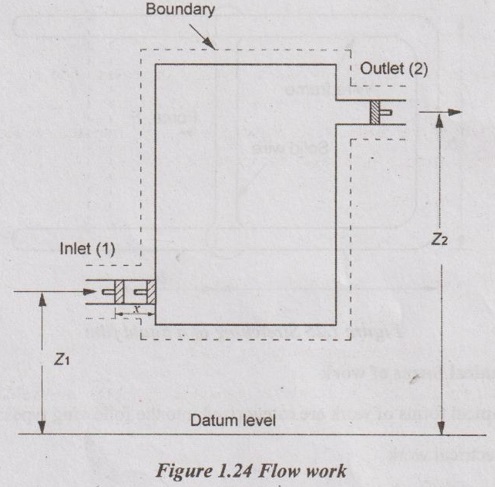
Similar to displacement work, the work done by fluid can be calculated by

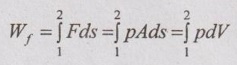
So, it can be written as

Wf = p(V2 - V1)         ...(1.23)

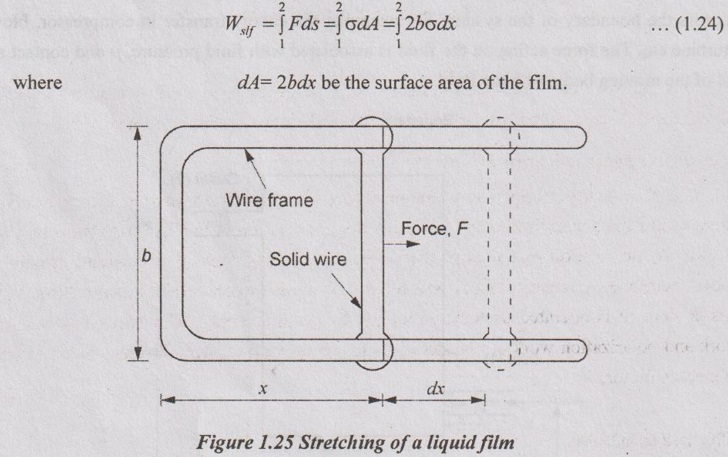
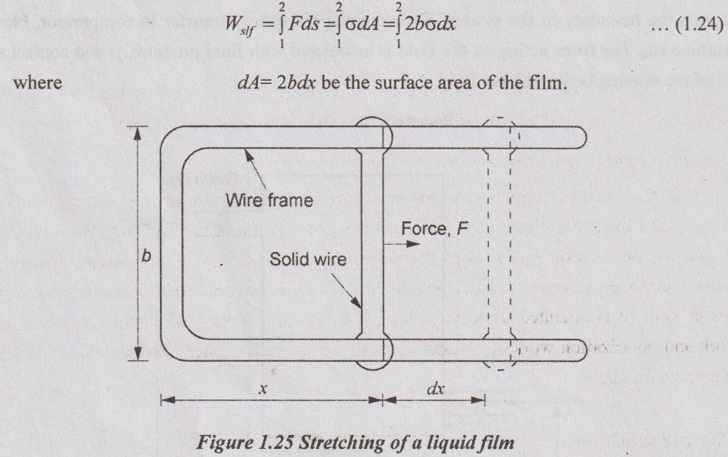
8. Work done associated with stretching of a liquid film:

Consider a liquid film such as a soap film suspended on a wire frame. Some force is needed to stretch this film by a movable portion of the wire frame. Actually, the force applied overcomes the bonding between molecules at the liquid-air interface. It is similar to the binding energy of atoms in a nucleus. This energy of molecules depends on the surface tension, σ (N/m) of liquid film. So, the work associated with the stretching of a film is also called surface tension work.

It can be calculated by

(b) Non-mechanical forms of work

Non-mechanical forms of work are categorized into the following types:

1. Electrical work

2. Magnetic work

3. Electrical polarization work.

1. Electrical work:

The flow of electrons is called electric current. The electrical work is calculated by using current and applied voltage. For example, the heat energy transferred by the heating coil is equal to the electrical energy supplied to heating element. So, the electrical work in kJ can be calculated by

2. Magnetic work:

It is the work performed in a system where the generalized force is the magnetic field strength and the generalized displacement is the total magnetic dipole moment.

3. Electrical polarization work:

It is the work performed in a system where the generalized force is the electric field strength and the generalized displacement is the polarization of the medium (the sum of the electric dipole rotation moments of the molecules). In any thermal equipment, usually the above-mentioned mechanical work transfer will occur due to concerned moving parts. When this equipment is operated or actuated mainly by electric supply, electrical work, magnetic work and polarization work are produced by magnetic field created between rotor and stator of electric motor.