Solved Problems on closed systems (Non-Flow Processes): Basics, Zeroth and First Law - Engineering Thermodynamics
SOLVED PROBLEMS ON CLOSED SYSTEMS (NON-FLOW PROCESSES)
Problem 1.12
Mass of 15 kg of air in a piston cylinder device is heated from 25°C to 90°C by passing current through a resistance heater inside the cylinder. The pressure inside the cylinder is held constant at 300 kPa during the process and a heat loss of 60 kJ occurs. Determine the electrical energy supplied in kW-hr and change in internal energy.-
Given data:
m = 15 kg
T1 = 25°C = 25 + 273 = 298 K
T2 = 90°C = 90 + 273 = 363 K
p1 = p2 = 300 kPa = 300 kN/m2
Q = -60 kJ
To find:
(i) Electrical energy supplied
(ii) Change in internal energy
Solution:
Work done,
W = mR (T2 - T1) = 15x0.287 (363-298) = 279.825 kJ
Electrical energy supplied
= Work done in kW-hr = Work done x 3600 = 279.825 × 3600=1007.37 x 103 kW-hr
Ans.
Change in internal energy,
AU=Q-W=-60-279.825 =-339.825 kJ Ans.
Problem 1.13
In a vessel 10 kg of O2 is heated in a reversible non-flow constant volume process so that the pressure of O2 is increased two times that of initial value. The initial temperature is 20°C. Calculate the final temperature, change in internal energy, change in enthalpy and heat transfer. Take R = 0.259 kJ/kg K and Cv = 0.625 kJ/kg K for oxygen.
Given data:
m = 10 kg
Process: Constant volume process
p2 = 2p1
T1 = 20°C = 20 + 273 = 293 K
R = Cp - Cv = 0.259 kJ/kg K
So, Cp = R + Cv = 0.259 + 0.652 = 0.911 kJ/kg K
To find:
T2, ΔU, ΔH and Q
Solution:
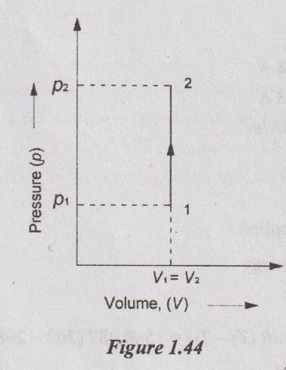
(a) Temperature at the end of the process (T2):
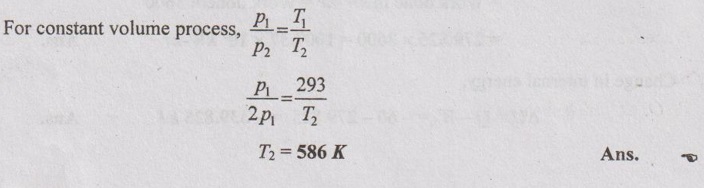
(b) Change in internal energy:
ΔU = m × Cv × (T2 – T1)
= 10 × 0.652 × (586 - 293)
= 1910.36 kJ Ans.
(c) Change in enthalpy:
ΔH = m × Cp × (T2 – T1)
= 10 × 0.911 × (586 - 293)
= 2669.23 kJ Ans.
By first law of thermodynamics,
Q = W + ΔU
For constant volume process,
W = 0
⸫ Q = ΔU = 1910.36 kJ Ans.
Problem 1.14
A certain gas of volume 0.4 m3, pressure of 4.5 bar and temperature of 130°C is heated in a cylinder to 9 bar when the volume remains constant. Calculate the (i) temperature at the end of the process, (ii) the heat transfer, (iii) change in internal energy (iv) work done by the gas, (v) change in enthalpy and (vi) mass of the gas. Assume Cp = 1.005 kJ/kgK and Cv = 0.71 kJ/kgK.
Given data:
V1 = 0.4 m3
p1 = 4.5 bar = 450 kN/m2
T1 = 130°C = 130 +273 = 403 K
p2 = 9 bar = 900 kN/m2
Cp = 1.005 kJ/kg K
Cv = 0.71 kJ/kg K and
Process: Constant volume process
To find:
T2, Q, ΔU, W, ΔH and m
Solution:
(a) Temperature at the end of the process (T2):
Relation between p, V and T for constant volume process is given by
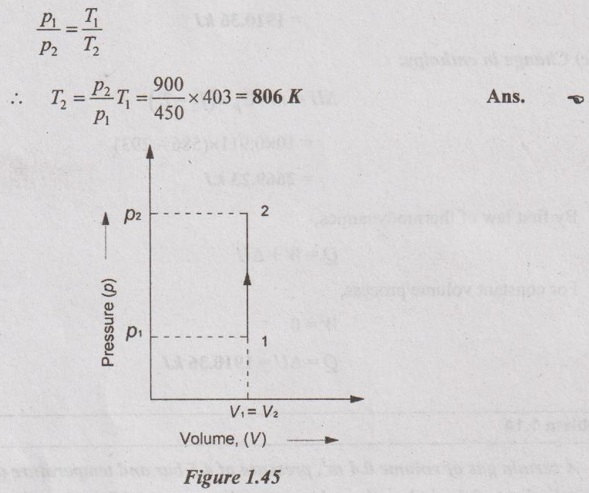
(b) Heat transfer (Q):
Q = mCv (T2 - T1)
First, the mass of the gas is found by using characteristic gas equation
p1V1 = mRT1
where R = Cp - Cv = 1.005 - 0.71 = 0.295 kJ/kgK
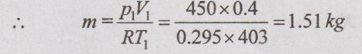
Then, Q = 1.51 × 0.71 × (806 - 403) = 432.06 kJ Ans.
(c) Change in internal energy, (ΔU):
From first law, Q = W + ΔU
In this process, W = 0
Therefore,
ΔU = Q = 433.2 kJ Ans.
(d) Work done by the gas (W):
For constant volume process, work done by the gas is zero.
W = 0 Ans.
(e) Change in enthalpy (H):
Enthalpy, ΔH = mCv (T2 - T1)
= 1.51 × 0.71 (806 - 403) = 432.06 kJ Ans.
(f) Mass of the gas (m):
Mass, m = 1.51 kg Ans.
Problem 1.15
5 kg of air at 40°C and 1 bar is heated in a reversible non-flow constant pressure until the volume is doubled. Find the (a) change in volume, (b) work done, (c) change in internal energy and (d) change in enthalpy.
Given data:
m = 5 kg
T1 = 40°C = 40 + 273 = 313 K
p1 = 1 bar = 100 kN/m2
V2 = 2V1
Process: Constant pressure process
To find:
V2 - V1, W, ΔU and ΔH
Solution:
From ideal gas equation,
p1V1 = mRT1
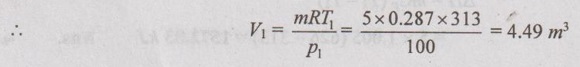
⸫ Final volume, V2 = 2V1 = 2 × 4.49 = 8.98 m3
(i) Change in volume:
V2 - V1 = 8.98 - 4.49 = 4.49 m3 Ans. 
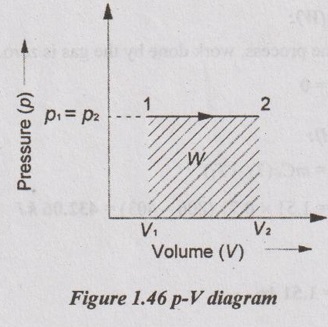
(ii) Work transfer:
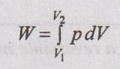
= p (V2 - V1)
= 100 (8.98 - 4.49) = 449 kJ Ans.
(iii) Change in internal energy:
ΔU = mCv (T2 - T1)
For constant pressure process,
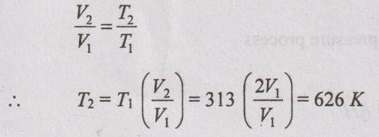
⸫ ΔU = 5 × 0.714 (626 - 313) = 1117.41 kJ Ans.
(iv) Change in enthalpy:
ΔH = mCp (T2 - T1)
= 5 × 1.005 (626 - 313) = 1572.83 kJ Ans.
Problem 1.16
One kg of gas expands at constant pressure from 0.085 m3 to 0.13 m3. If the initial temperature of the gas is 225°C, find the final temperature, net heat transfer, change in internal energy and pressure of gas.
Given data:
Process: Constant pressure process
m = 1 kg
V1 = 0.085 m3
V2 = 0.13 m3
T1 = 225°C = 225 + 273 = 498 K
Assume Cp = 1.005 kJ/kg K; Cv = 0.718 kJ/kg K
To find:
T2, Q, ΔU and p
Solution:
(i) Final temperature (T2):
By using p, V and T relation for constant pressure process,
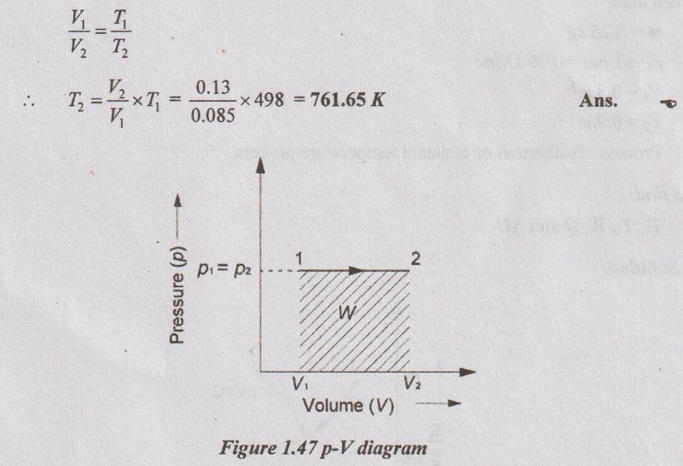
(ii) Heat transfer (Q):
Q = mCp (T2 - T1) = 1 × 1.005 (761.65 - 498) = 264.97 kJ Ans.
(iii) Change in internal energy (ΔU):
ΔU = mCv (T2 – T1) = 1 × 0.718 (761.65 - 498) = 189.3 kJ Ans.
(iv) Pressure (p):
p1V1 = mRT1
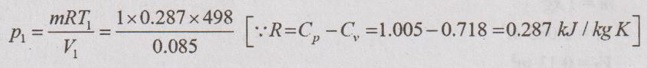
p1 = 1681.48 kN/m2 = p2 Ans.
Problem 1.17
0.25 kg of air at a pressure of 1 bar occupies a volume of 0.3 m3. If this air expands isothermally to a volume of 0.9 m3, find the (i) initial temperature, (ii) final temperature (iii) external work done, (iv) heat absorbed by the air and (v) change in internal energy. Assume R = 0.287 kJ/kgK.
Given data:
m = 0.25 kg
p1 = 1 bar = 100 kN/m2
V1 = 0.3 m3
V2 = 0.9 m3
Process: Isothermal or constant temperature process
To find:
T1, T2, W, Q and ΔU
Solution:
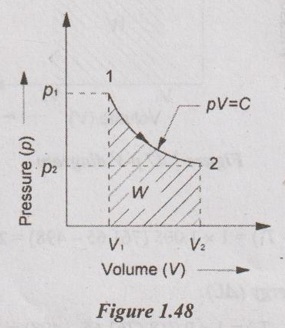
From ideal gas equation,
p1V1 = mRT1
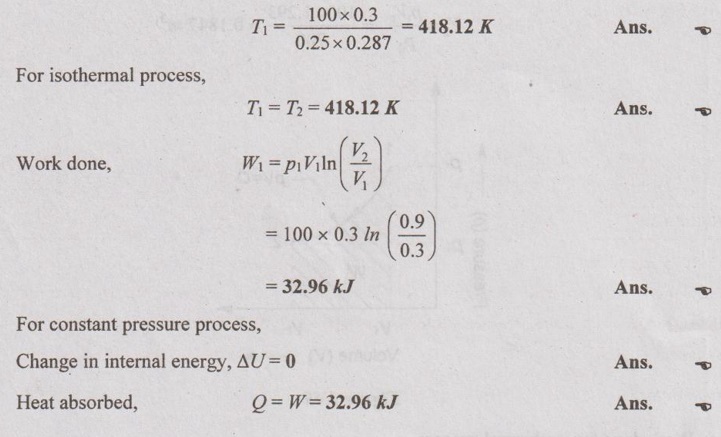
Problem 1.18
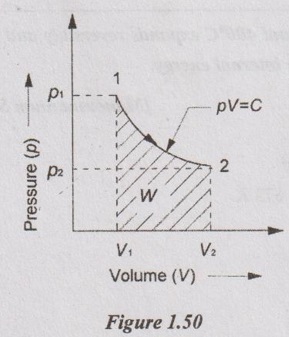
A mass of 1.5 kg of air is compressed in a quasi-static process from 0.1 MPa to 0.7 MPa for which pV = constant. The initial density of air is 1.16 kg/m3. Find the work done by the piston to compress the air.
Given data:
m = 1.5 kg
Process = quasi-static, pV= C (Isothermal)
p1 = 0.1 MPa = 100 kN/m2
p2 = 0.7 MPa = 700 kN/m2
Initial density, ρ1 = 1.16 kg/m3
To find:
Work done, W
Solution:
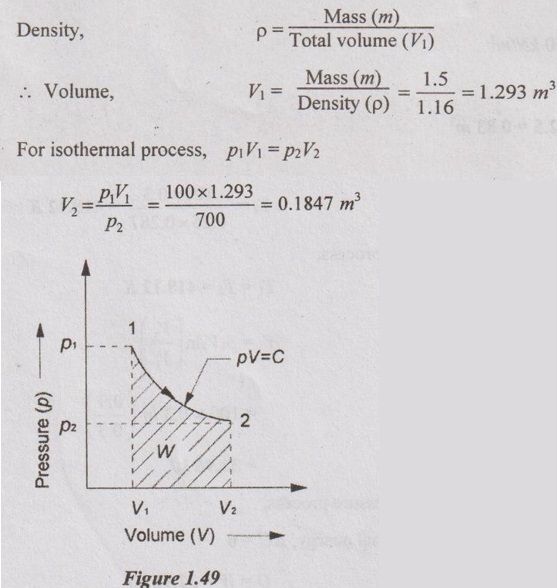
Work done for isothermal process,
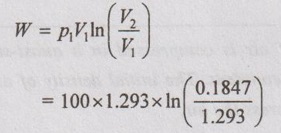
= -251.62 kJ Ans.
(Negative sign indicates that the work is done on the system)
Problem 1.19
2 kg of gas at a pressure of 1.5 bar occupies a volume of 2.5 m3. If this gas is isothermally compressed to 1/3 times the initial volume, find the (i) initial temperature (ii) final temperature (iii) work done and (iv) heat transfer. Assume R = 0.287 kJ/kgK.
Given data:
m = 2 kg
p1 = 1.5 bar = 150 kN/m2
V1 = 2.5 m3
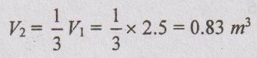
R = 0.287 kJ/kgK
Process: Isothermal or Constant temperature process
To find:
T1, T2, W and Q
Solution:
(i) Initial and final temperatures (T1 and T2):
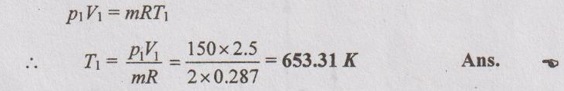
(ii) Wok done (W):
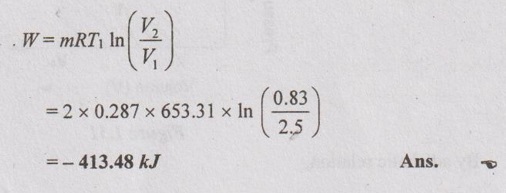
Note: Here, negative sign indicates that the work is done on the system.
(iii) Heat transfer (Q):
From first law, Q = W + ΔU
For isothermal process, ΔU = 0
⸫ Q = W = -413.48 kJ Ans.
Note: Here negative sign indicates that the heat is rejected by the system.
Problem 1.20
10 kg of gas at 10 bar and 400°C expands reversibly and adiabatically to 1 bar. Find the work done and change in internal energy.
Given data:
m = 10 kg
p1 = 10 bar = 1000 kN/m2
T1 = 400°C = 400 + 273 = 673 K
p2 = 1 bar = 100 kN/m2
To find:
W and ΔU
Solution:
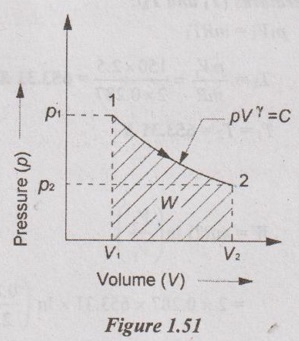
By adiabatic relation,
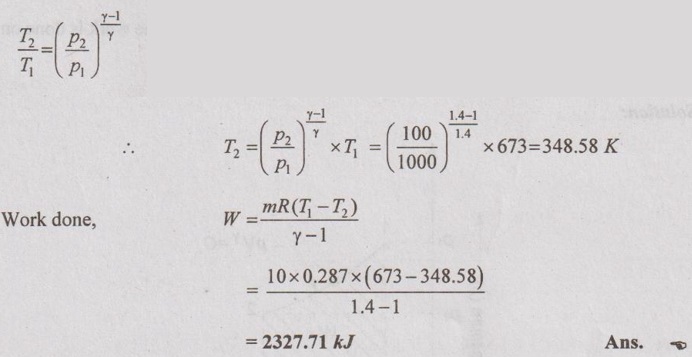
Change in internal energy,
ΔU = m × Cv × (T2 – T1)
= 10 × 0.718 × (348.58 - 673)
= -2329.34 kJ Ans.
Alternately, from first law, Q = W + ΔU
In adiabatic process, Q = 0
⸫ ΔU = -W = -2329.34 kJ Ans.
Problem 1.21
1.5 kg of certain gas at a pressure of 8 bar and 20°C occupies the volume of 0.15 m3. It expands adiabatically to a pressure of 0.9 bar and volume 0.73 m3. Determine the work done during the process, gas constant, ratio of the specific heats, values of two specific heats, change in internal energy and change in enthalpy.
Given data:
m = 1.5 kg
p1 = 8 bar = 800 kN/m3
V1 = 0.15 m3
T1 = 20°C = 20 + 273 = 293 K
p2 = 0.9 bar = 90 kN/m2
V2 = 0.73 m3
To find:
W, R, Cp/Cv, Cp, Cv, ΔU and ΔH
Solution:
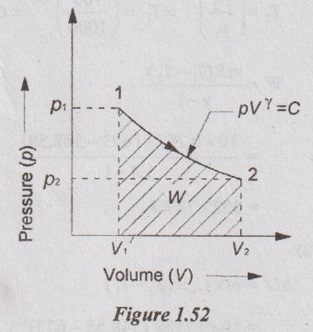
From characteristic gas equation
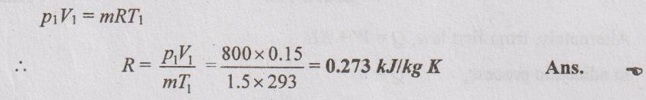
Ratio of specific heats,
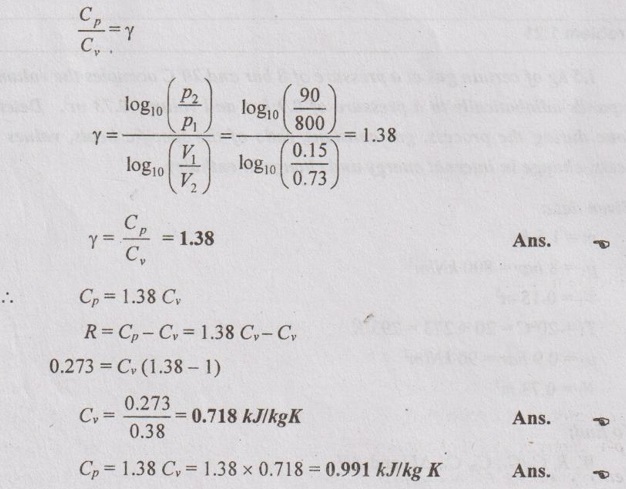
By using the relation between T and V for isentropic process,
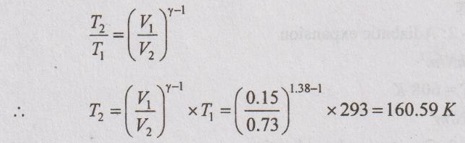
Change in internal energy (ΔU):
ΔU = mCv (T2 - T1)
= 1.5 × 0.718 × (160.59 - 293) = -142.61 kJ Ans.
Change in enthalpy (ΔH):
ΔH = mCp (T2 - T1)
= 1.5 × 0.991 × (160.59 - 293) = -196.83 kJ Ans.
Work done (W):
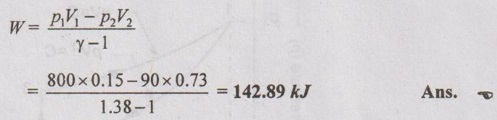
Alternately, from first law of thermodynamics,
Q = W + ΔU
For isentropic process, Q = 0
⸫ W = -ΔU = 142.61 kJ Ans.
Problem 1.22
A gas of mass 0.35 kg with pressure of 1535 kN/m2 and temperature of 335°C is expanded adiabatically to a pressure of 126 kN/m2. The gas is then heated at constant volume until it reaches 335°C when its pressure is found to be 275 kN/m2. Finally the gas is compressed isothermally until the original pressure of 1535 kN/m2 obtained. Draw the p-V diagram and find out the following (i) value of adiabatic index, (ii) change in internal energy during adiabatic process and (iii) heat transfer during constant volume process. Take Cp = 1.005 kJ/kgK.
Given data:
m = 0.35 kg
Process 1-2: Adiabatic expansion
p1 = 1535 kN/m2
T1 = 335°C = 608 K
p2 =126 kN/m2
Process 2-3: Constant volume heating
T3 = T1 = 608 K
p3 = 275 kN/m2
Process 31: Isothermal compression
To find:
γ, ΔU and Q
Solution:
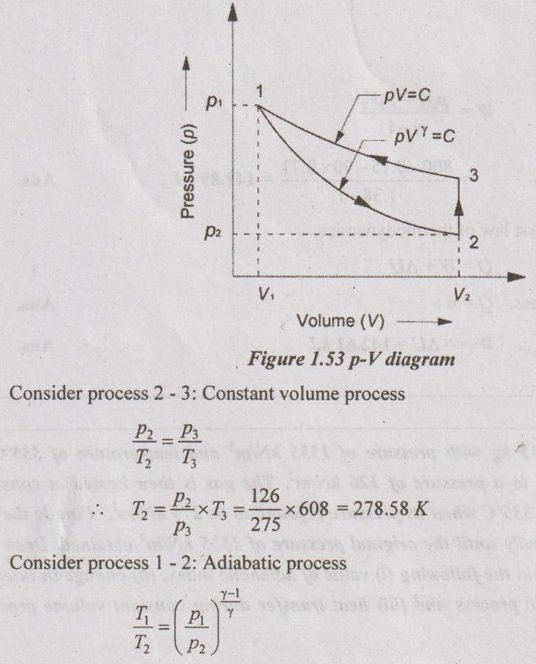
Taking log on both sides,
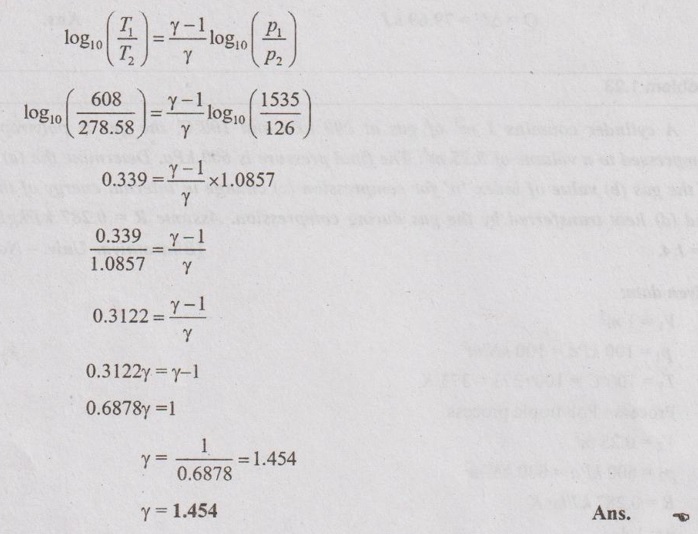
Change in internal energy (ΔU) during adiabatic process,

Heat transfer during constant volume process,
Q = mCv (T3 - T2)
= 0.35 × 0.691 × (608 - 278.58) = 79.67 kJ Ans.
Alternatively, from first law of thermodynamics,
Q = W + ΔU
Since work done during constant volume process is zero, i.e. W = 0
Q = ΔU = 79.69 kJ Ans.
Problem 1.23
A cylinder contains 1 m3 of gas at 100 kPa and 100°C, the gas is polytropically compressed to a volume of 0.25 m3. The final pressure is 600 kPa. Determine the (a) mass of the gas (b) value of index 'n' for compression (c) change in internal energy of the gas and (d) heat transferred by the gas during compression. Assume R = 0.287 kJ/kgK and γ = 1.4.
Given data:
V1 = 1 m3
p1 = 100 kPa = 100 kN/m2
T1 = 100°C = 100 + 273 = 373 K
Process: Polytropic process
V2 = 0.25 m3
p2 = 600 kPa = 600 kN/m2
R = 0.287 kJ/kg K
γ = 1.4
To find:
m, n, ΔU and Q
Solution:
By general gas equation,

The value of index 'n' is given by
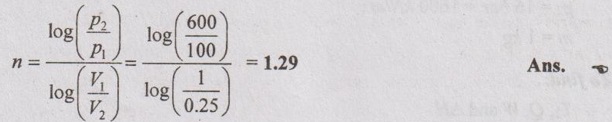
From polytropic equation,
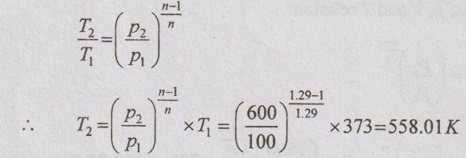
Change in internal energy,
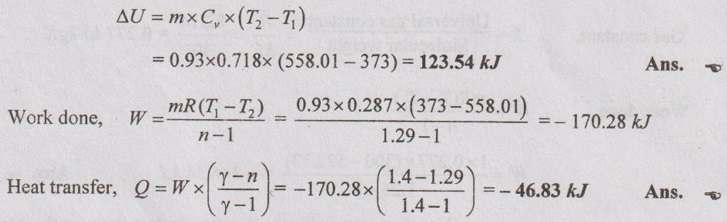
Problem 1.24
An ideal gas of molecular weight 30 and specific heat ratio 1.4 is compressed according to the law pV1.25 = C from 1 bar absolute and 27°C to a pressure of 16 bar (abs). Calculate the temperature at the end of compression, heat received or rejected, work done on the gas during the process and change in enthalpy. Assume mass of the gas as 1 kg.
Given data:
Molecular weight, M = 30
Cp / Cv = γ = 1.4
pV1.25 = C
p1 = 1 bar = 100 kN/m2
T1 = 27°C = 27 + 273 = 303 K
p2 = 16 bar = 1600 kN/m2
m = 1 kg
To find:
T2, Q, W and ΔH
Solution:
For polytropic process, p, V and T relation
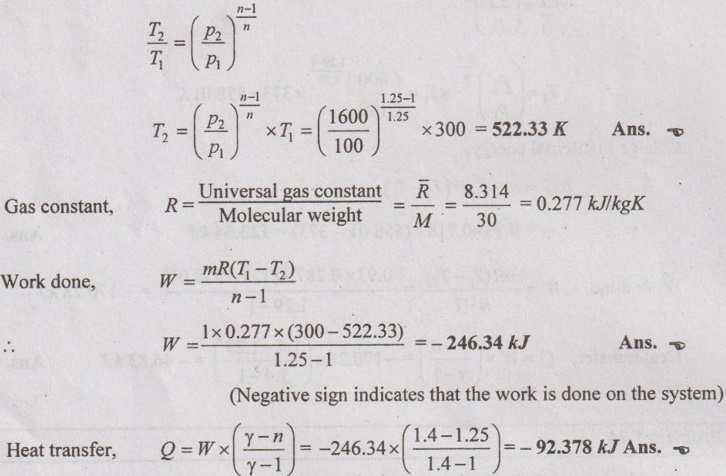 (Negative sign indicates that the heat is rejected from the system)
(Negative sign indicates that the heat is rejected from the system)
ΔH = m × Cp × (T2 – T1)
= 1 × 1.005 × (522.33 - 300) = 233.4 kJ Ans.
Problem 1.25
A perfect gas for which the ratio of specific heats is 1.4 occupies a volume of 0.3 m3 at 100 kPa and 27°C. The gas is compressed to 0.06 m3. Find the heat transfer during the compression for the following methods (a) pV = constant, (b) isentropic and (c) pv1.1 = C.
Given data:
γ = 1.4
p1 = 100 kPa = 100 kN/m2
V1 = 0.3 m3
T1 = 27°C + 273 = 300 K
V2 = 0.06 m3
Processes: (i) pV = C
(ii) pVγ = C and
(iii) pV1.1 = C.
To find:
Heat transfer (Q)
Solution:
(a) pV = C
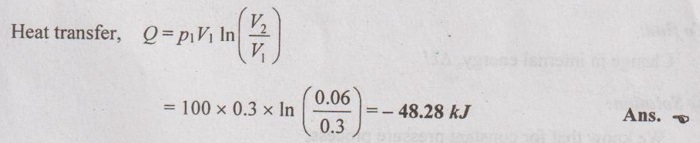
(b) pVγ = C
Heat transfer, Q = 0 Ans.
(c) pV1.1 = C
From polytropic relation,
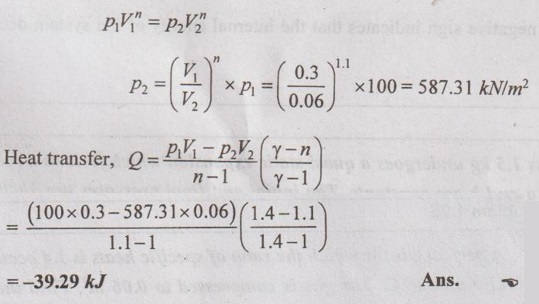
No comments:
Post a Comment