Solved Problems on open systems or control volume for Steady Flow

 Solved Problems on open systems or control volume for steady flow: Basics, Zeroth and First Law - Engineering Thermodynamics

SOLVED PROBLEMS ON OPEN SYSTEMS OR CONTROL VOLUME FOR STEADY FLOW

Problem 1.26

In a steady flow process, 125 kJ of work is done by each kg of working fluid. The specific volume, velocity and pressure of the working fluid at inlet are 0.41 m3/kg, 15.5 m/s and 6 bar respectively. The inlet is 31 m above the ground and the exhaust pipe is at the ground level. The discharge conditions of the working fluid are 0.64 m3/kg, 1 bar and 263 m/s. The total heat loss between inlet and discharge is 8.7 kJ/kg of fluid. In flowing through this apparatus, does the specific internal energy increase or decrease and by how much?

Given data:

W = 125 kJ/kg

v1 = 0.41 m3/kg

C1 = 15.5 m/s

p1 = 6 bar = 600 kN/m2

z1 = 31 m

z2 = 0

v2 = 0.64 m3/kg

C2 = 263 m/s

p2 = 1 bar = 100 kN/m2

Q = -8.7 kJ/kg (⸪ Heat loss)

To find:

Whether the internal energy increases or decreases and how much.

Solution:

The steady flow energy equation is given by

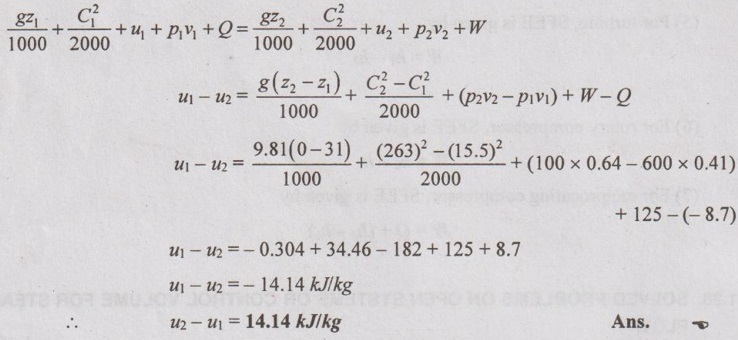
Problem 1.27

50 kg/min of air enters the control volume in a steady flow system at 2 bar and 100°C and at an elevation of 100 m above the datum. The same mass leaves the control volume at 150 m elevation with a pressure of 10 bar and the temperature of 300°C. The entrance velocity is 2400 m/min and the exit velocity is 1200 m/min. During the process, 50000 kJ/hr of heat is transferred to the control volume and the rise in enthalpy is 8 kJ/kg. Calculate the power developed. 

Given data:

m = 50 kg/min = 50/60 = 0.83 kg/s

p1 = 2 bar = 200 kN/m2

T1 = 100°C = 100 + 273 = 373 K

z1 = 100 m

z2 = 150 m

p2 = 10 bar = 1000 kN/m2

T2 = 300°C = 300 + 273 = 573K

To find:

Power developed, P

Solution:

SFEE is given by

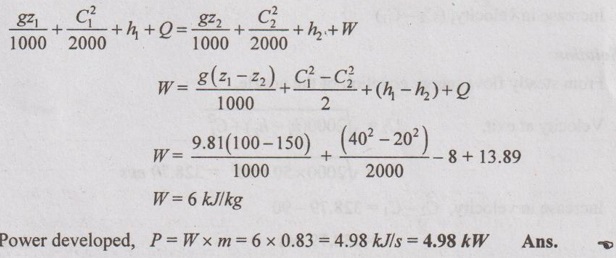
Problem 1.28

A boiler produces steam from water at 35°C. The enthalpy of steam is 2675 kJ/kg. Calculate the heat transferred per kg. The specific heat capacity of water is 4.19 kJ/kg. Neglect the potential and kinetic energies.

Given data:

Tw = 35°C = 35 + 273 = 308 K

h2 = 2675 kJ/kg

Cpw = 4.19 kJ/kg K

To find:

Heat transferred, Q

Solution:

Enthalpy of feed water, h1 = CpwTw = 4.19 × 308 = 1290.52 kJ/kg

SFEE for boiler, heat transferred (Q),

Q = h2 - h1 = 2675 - 1290.52 = 1384.48 kJ/kg Ans.

Problem 1.29

In a steady flow of air through a nozzle, the enthalpy decreases by 50 kJ between two sections. Assuming that there are no other energy changes than the kinetic energy, determine the increase in velocity at section 2 if the initial velocity is 90 m/s.

Given data:

Enthalpy decrease, (h1 – h2) = 50 kJ = 50000 J

Velocity at section (1), C1 = 90 m/s

To find:

Increase in velocity, (C2 - C1)

Solution:

From steady flow energy equation of the nozzle,

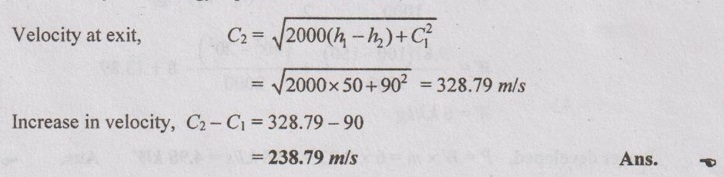
Problem 1.30

At the inlet of the nozzle, the enthalpy and velocity of the fluid are 3000 kJ/kg and 50 m/s respectively. There is negligible heat loss from the nozzle. At the outlet of the nozzle, enthalpy is 2450 kJ/kg. If the nozzle is horizontal, find the velocity of the fluid at exit.

Given data:

h1 = 3000 kJ/kg

C1 = 50 m/s

Q = 0

z1 = z2

h2 = 2450 kJ/ kg

To find:

Velocity of the fluid at exit, C2

Solution:

From steady flow energy equation of the nozzle,

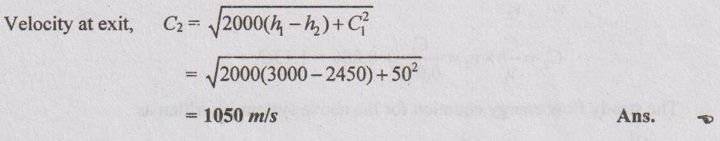
Problem 1.31

In a thermal power station, the steam flows steadily through a 0.3 m diameter pipeline from boiler to turbine. A boiler exhausts the steam at a pressure of 4.2 bar, the temperature of 420°C and the enthalpy of 3216.3 kJ/kg. The specific volume of the steam boiler at outlet is 0.076 m3/kg. After flowing through the turbine, the steam conditions are measured as the pressure of 3.1 bar, the temperature of 379°C, the enthalpy of 3201.7 kJ/kg and the specific volume of 0.086 m3/kg. There is a heat loss of 8.3 kJ/kg from the pipeline between boiler and turbine. Calculate the rate of flow of steam.

Given data:

d1 = 0.3 m

p1 = 4.2 bar = 420 kN/m2

T1 = 420°C

h1 = 3216.3 kJ/kg

v1 = 0.076 m3/kg

p2 = 3.1 bar = 310 kN/m2

T2 = 379°C

h2 = 3201.7 kJ/kg

v2 = 0.086 m3/kg

Q = -8.3 kJ/kg (⸪ Heat loss)

To find:

Rate of flow of steam, m

Solution:

By mass flow equation,

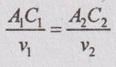
Since the pipe diameter 0.3 m is constant (A1 = A2),

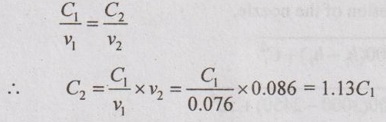
The steady flow energy equation for the above system is written as

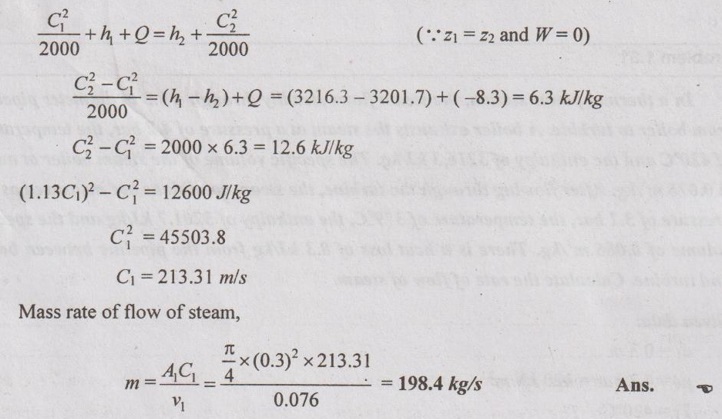
Problem 1.32

A turbine operates under steady flow conditions receiving steam at the following state: pressure = 1.2 MPa, temperature = 188°C, enthalpy = 2785 kJ/kg, velocity= 33.3 m/s and elevation = 3 m. The steam leaves the turbine at the following state: pressure = 20 kPa, enthalpy = 2512 kJ/kg, velocity = 100 m/s and elevation = 0 m. Heat is lost to the surroundings at the rate of 0.29 kJ/s. If the rate of steam flow through the turbine is 0.42 kg/s, what is the power output of the turbine in kW?

Given data:

p1 = 1.2 MPa

T1 = 188°C = 188 + 273 = 461 K

h1 = 2785 kJ/kg

C1 = 33.3 m/s

z1 = 3 m

p2 = 20 kPa

h2 = 2512 kJ/kg

C2 = 100 m/s

z2 = 0 m

Q = -0.29 kJ/s (⸪ Heat loss)

m = 0.42 kg/s

To find:

Power output, W

Solution:

As per SFEE,

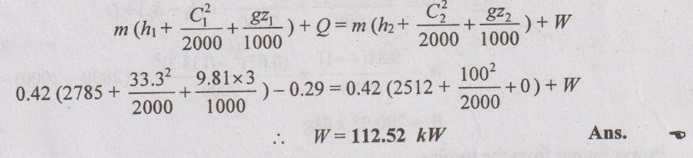
Problem 1.33

A steam turbine operates under steady flow conditions. It receives steam 7200 kg/hr from the boiler. The steam enters the turbine at enthalpy of 2800 kJ/kg, a velocity of 400 m/min and an elevation of 4 m. The steam leaves the turbine at enthalpy of 2000 kJ, a velocity of 8000 m/min and an elevation of 1 m. Due to radiation, the amount of heat losses from the turbine to the surrounding is 1580 kJ/hr. Calculate the power output of the turbine. 

Given data:

To find:

Power output of the turbine, P

Solution:

The SFEE for the above system is given by

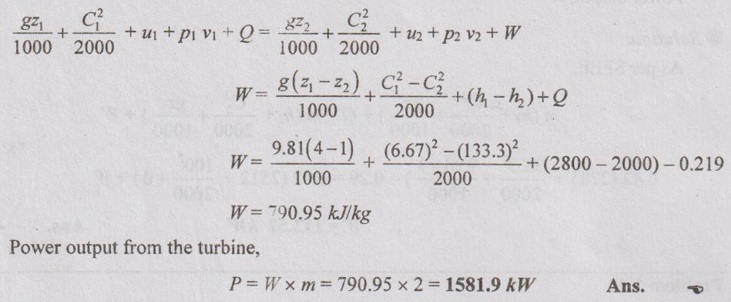
Problem 1.34

Air flows steadily at the rate of 0.5 kg/s through an air compressor entering at 7 m/s velocity, 100 kPa pressure and 0.95 m3/kg, volume and leaving at 5 m/s, 700 kPa and 0.19 m3/kg. The internal energy of the air leaving is 90 kJ/kg greater than the air entering. The cooling water in the compressor jackets absorbs heat from the air at the rate of 58 kW. (a) Compute the rate of shaft work input to the air in kW. (b) Find the ratio of the inlet pipe diameter to the outlet pipe diameter.

Given data:

m = 0.5 kg/s

C1 = 7 m/s

p1 = 100 kPa

v1 = 0.95 m3/kg

C2 = 5 m/s

p2 = 700 kPa

v2 = 0.19 m3/kg

u2 - u1 = 90 kJ/kg 

Q = -58 kW

To find:

Work input, W and D1 / D2

Solution:

SFEE is given by

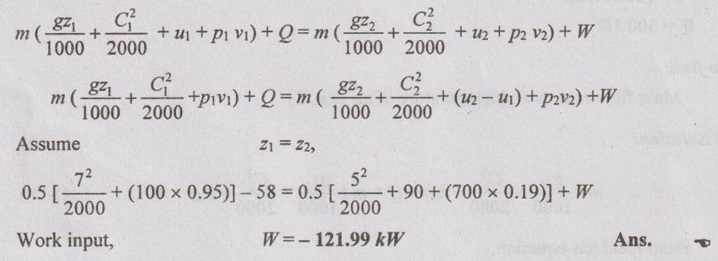
(⸪ Negative sign indicates that the work is done on the system)

From continuity equation,

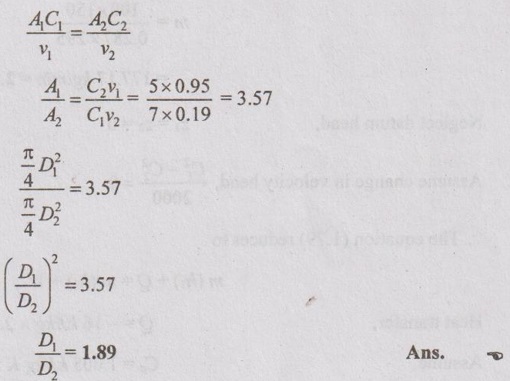
Problem 1.35

Air is compressed from 100 kPa and 22°C to a pressure of 1 MPa while being cooled at the rate of 16 kJ/kg by circulating water through the compressor casing. The volume flow rate of air inlet condition is 150 m3/min and power input to compressor is 500 kW. Determine the (a) mass flow rate (b) temperature of air exit. Neglect datum head.

Given data:

p1 = 100 kPa

T1 = 22°C = 22 + 273 = 295 K

p2 = 1 MPa

Q = - 16 kJ/kg

V1 = 150 m3/min

W = 500 kW

To find:

Mass flow rate, m and temperature of air exit, T2

Solution:

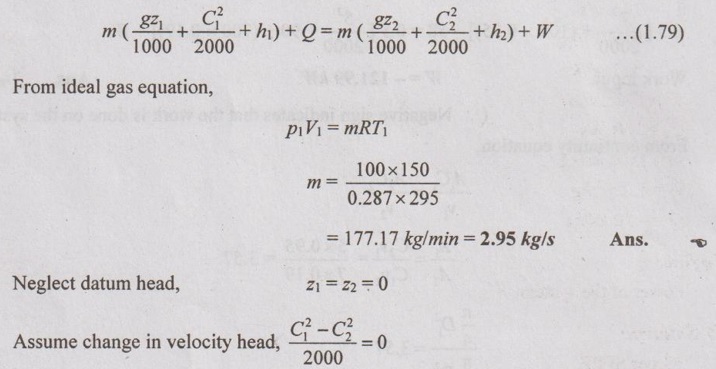
⸫ The equation (1.79) reduces to

m (h1) + Q = m (h2) + W

Heat transfer, Q =-16 kJ/kg × 2.95 kg/s = 47.2 kW

Assume Cp = 1.005 kJ/kg K for air

⸫ m (CpT1) + Q = m (CpT2) + W

2.95 (1.005 × 295) - 47.2 = 2.95 (1.005 × T2) - 500

T2 = 447.7 K    Ans.