Problem 1.36
An insulated rigid tank with zero heat capacity contains 15 kg of air at 2 bar and 50°C. It is filled with air from a large reservoir at 10 bar and 60°C. Find the final state of air in the tank and mass added. Assume Cp = 1.03 kJ/kgK and Cv = 0.71 kJ/kgK.
Given data:
For insulated tank, Q = 0
For rigid tank, V1 = V2
m1 = 15 kg
p1 = 2 bar
T1 = 50°C = 50 + 273 = 323 K
p2 = 10 bar
Tr = 60°C = 60 + 273 = 333 K
Cp = 1.03 kJ/kgK
Cv = 0.71 kJ/kgK
To find:
T2 and mass added (m2 – m1)
Solution:
From ideal gas equation,
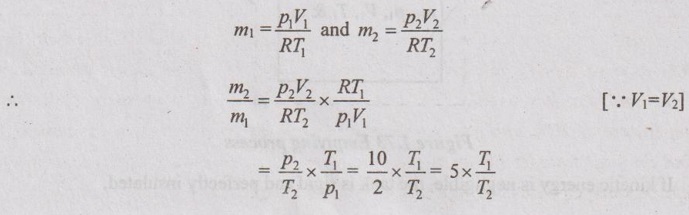
From unsteady flow energy equation
Q - W = m2u2 – m1u1 - (m2 – m1) h1 …..(1.87)
Q = 0 for insulated tank
W = 0 for rigid tank
⸫ The equation (1.87) becomes
m2u2 – m1u1 - (m2 – m1) h1 = 0
Then, the equation becomes
m2 CvT2 – m1CvT1 - (m2 – m1) CpTr = 0
Dividing the above equation by m1 on both sides,
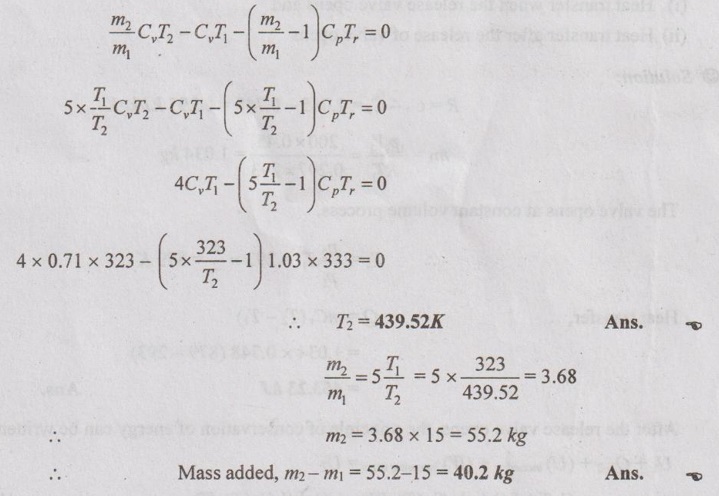
Problem 1.37
A tank of volume 0.45 m3 contains an electric heating coil but it is thermally insulated. The tank is equipped with a release valve which allows the gas to escape when the pressure in the tank reaches 6 bar. The tank is filled with O2 at a pressure of 2 bar and a temperature of 20°C and gas is then heated until the temperature in the tank is 1140°C. Find the heat transfer (a) up to the time when the release valve opens and (b) after this time. Assume Cp =1.045 kJ/kgK and Cv = 0.748 kJ/kgK.
Given data:
V1 = 0.45 m3
For insulated tank, Q = 0
p2 = 6 bar
p1 = 2 bar = 200 kPa
T1 = 20°C = 20 + 273 = 293 K
T3 = 1140 + 273 = 1413 K
Cp = 1.045 kJ/kgK
Cv = 0.748 kJ/kgK
To find:
(i) Heat transfer when the release valve opens and
(ii) Heat transfer after the release of valve opens
Solution:
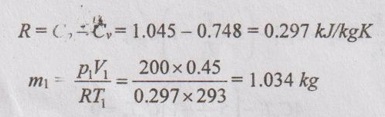
The valve opens at constant volume process.
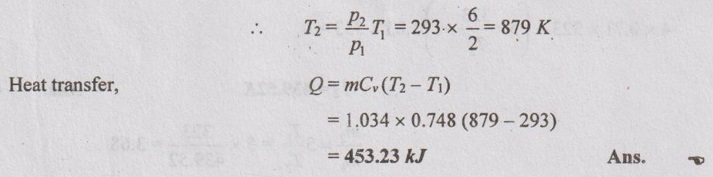
After the release valve opens, the principle of conservation of energy can be written as
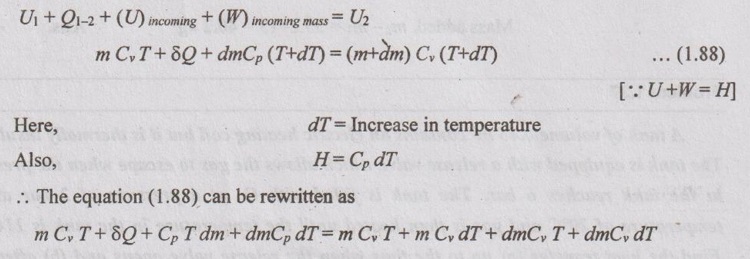The values dmCp dT and dmCv dT are too small when compared to other quantities in the same equation. So, it is neglected. Therefore,
Problem 1.38
An insulated and rigid vessel contains 16 m3 of air at 20 bar and 200°C. This allows to expand to 2 bar. Find the maximum work that can be obtained from the escaping air in an adiabatic process. Take γ = 1.4, Cp = 1.005 kJ/kgK and Cv = 0.718 kJ/kgK.
Given data:
V1 = 16 m3 = V2 for rigid vessel
For insulated vessel, Q = 0
p1 = 20 bar = 2000 kPa
T1 = 200°C = 200 + 273 = 473 K
p2 = pr = 2 bar = 200 kPa.
γ = 1.4
Cp = 1.005 kJ/kgK
Cv = 0.718 kJ/kgK
To find:
Maximum work, W
Solution:
The unsteady flow energy equation is given by
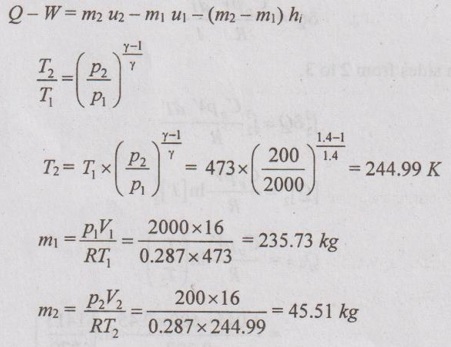
The unsteady flow energy equation,
Q – W = m2 u2 – m1 u1 - (m2 - m1) Cp Tr
Q = 0 for insulated tank
-W = m2 Cv T2 – m1 Cv T1 - (m2 - m1) Cp Tr
-W = 45.51 × 0.718 × 244.99 - 235.73 × 0.718 × 473
-(45.51 - 235.73) × 1.005 × 244.99
W = 25216.86 kJ Ans.
Problem 1.39
In an internal combustion engine at the end of the exhaust stroke, its combustion chamber is filled with 0.00044 kg of exhaust gas at 650 K at atmospheric pressure. The piston then descends during intake stroke for sucking 0.002 kg of air at 300 K in the cylinder. If the suction process is assumed to take place at constant atmospheric pressure and if the heat transfer is negligible, find the temperature and pressure of the mixture at the end of the intake stroke.
Given data:
m1 = 0.00044 kg
m2 = 0.002 kg
T1 = 650 K
Tr = 300 K
Q = 0
To find:
Final temperature, T2 and final pressure, p2
Solution:
Since the suction process takes place at constant pressure,
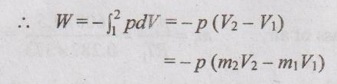
The unsteady flow energy equation,
Q – W = m2u2 – m1u1 - (m2 - m1) h1
Here, there is no heat interaction, Q = 0
So, the equation reduces to
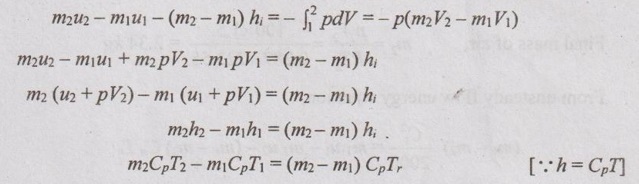
0.002 × 1.005 × T2 - 0.00044 × 1.005 × 650 = (0.002 - 0.00044) × 1.005 × 300
T2 = 377 K Ans.
Suction pressure,
p2 = 1 atm (given in the Problem itself) Ans.
No comments:
Post a Comment