Heat Engines, Refrigerators and Heat Pump - Solved Problems

Solved Problems on Heat Engines, Refrigerators and Heat Pump: Second Law and Entropy - Engineering Thermodynamics

SOLVED PROBLEMS ON HEAT ENGINES, REFRIGERATORS AND HEAT PUMP

Problem 2.1

An inventor claims to have developed an efficient heat engine which would have a heat source at 1000°C and reject heat to a sink at 50°C and gives an efficiency of 90%. Justify whether his claim is possible or not.

Given data:

T1 = 1000°C = 1000 + 273 = 1273 K

T2 = 50°C = 50 + 273 = 323 K

η = 90%

To find:

Whether the inventor's claim is correct or not.

Solution:

According to Carnot theorem, the reversible engine gives maximum efficiency than all other heat engines.

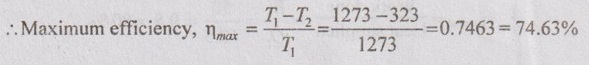
Maximum efficiency (74.63%) is less than the proposed engine efficiency (90%). Therefore, the inventor's claim is impossible.      Ans.

Problem 2.2

An inventor claims that his proposed engine has the following specification:

Power developed = 50 kW

Fuel burnt = 3 kg/hr

Calorific value of the fuel = 75000 kJ/kg

Temperature limits = 27°C and 627°C

Find out whether it is possible or not.

Given data:

W = 50 kW

Fuel burnt = 3 kg/hr

Calorific value (CV) of fuel = 75,000 kJ/kg

Temperature limits, T2 = 27°C = 27 + 273 = 300 K

T1 = 627°C = 627 + 273 = 900 K

To find:

Whether the inventor's claim is possible or not.

Solution:

Heat supplied to the engine, Q1 = Fuel burnt × CV

= 3 × 75000

= 225000 kJ/hr

Q1= 62.5 kJ/s = 62.5 kW

Work done, W = 50 kW

From Carnot theorem, Carnot engine gives maximum efficiency than any other engine.

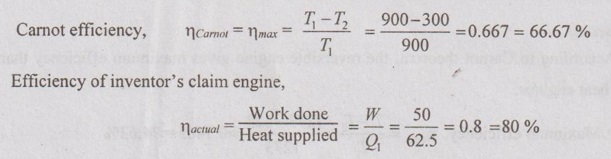
Here the inventor's claim engine has the higher efficiency than maximum engine efficiency which is impossible.           Ans.

Problem 2.3

Determine whether the following cases represent the reversible, irreversible or impossible heat engines:

(i) 900 kW of heat rejected

(ii) 560 kW of heat rejected

(iii) 108 kW of heat rejected

In each case the engine is supplied with 1120 kJ/s of heat. The source and sink temperature are maintained at 560 K and 280 K.

Given data:

T1 = 560 K

T2 = 280 K

Q1 = 1120 kJ/s

(i) Q2 = 900 kW

(ii) Q2 = 560 kW

(iii) Q2 = 108 kW

To find:

Conclude the above cases are reversible, irreversible and impossible heat engines.

Solution:

From Carnot theorem, the Carnot engine gives maximum efficiency than any other engine.

Maximum efficiency or Carnot efficiency,

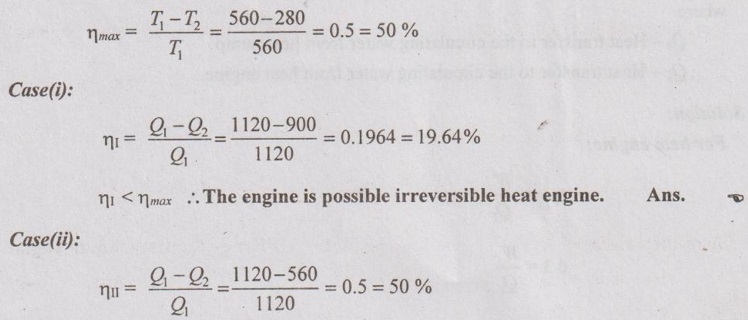
But, engine C directly rejects heat to the low temperature reservoir, T4. The intermediate temperature between engine A and B is T2 = T3 = T.

Applying the above equation (2.3) for all three engines A, B and C respectively,

pppppp

So, the equation can be rewritten by using equations (2.5) and (2.6) as follows,

pppppp

The above equation (2.9) is a function of T1 and T4 only and it is independent of T on left hand side. The right hand side is also a function of T1 and T4 but it is not independent of T. The product of T gets cancelled. After it has been cancelled, the term f (T1, T) can be written as ϕ(T1)/ϕ(T) and the term ƒ (T, T4) can be written as ϕ(T)/ϕ( T4), where ϕ is another unknown function.

pppp

This obeys Kelvin-Planck statement of second law of thermodynamics. So, it can be written as ϕ(T) = T. Then the above equation becomes

pppp

This temperature scale is known as Kelvin scale. The temperature measured on this scale is known as absolute temperature.

The temperature scale is not completely defined. At International Conference on Weights and Measures (1954), the triple-point of water was assigned as the value of 273.16 K. The magnitude of a Kelvin is defined as 1/273.16 of the temperature interval between absolute zero and triple- point temperature of water. The magnitudes of temperature units on the Kelvin and Celsius scales are identical (1 K = 1°C). The temperatures on these two scales differ by a constant 273.16.

T(°C) = T(K) - 273.16

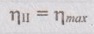
Therefore, it is reversible heat engine because by II law all the reversible engines have same efficiency.   Ans.

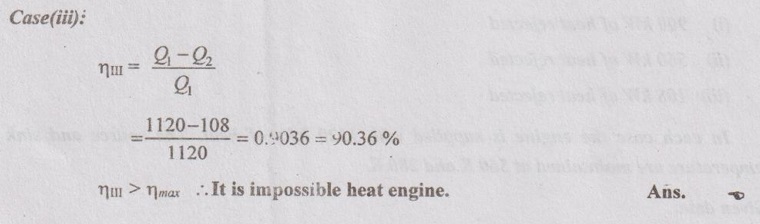
Problem 2.4

A heat engine of 30% efficiency drives a heat pump of COP = 5. The heat is transferred both from engine and heat pump to the circulating water for heating the building in winter. Find the ratio of heat transfer to the circulating water from the heat pump to the heat transfer to the circulating water from the heat engine.

Given data:

ηHE 30%

COP of HP = 5

To find:

Q4/Q1

where

Q4 - Heat transfer to the circulating water from heat pump Q1 - Heat transfer to the circulating water from heat engine.

Solution:

For heat engine:

For heat pump:

Problem 2.5

A reversible heat engine operating between reservoirs at 900 K and 300 K drives a reversible refrigerator operating between reservoirs at 300 K and 250 K. The heat engine receives 1800 kJ heat from 900 K reservoir. The net output from the combined engine refrigerator is 360 kJ. Find the heat transferred to the refrigerator and net heat rejected to the reservoir at 300 K.

Given data:

T1 = 900 K

T2 = 300 K

T4 = 250 K

T3 = 300 K

Q1 = 1800 kJ

W1 - W2 = 360 kJ

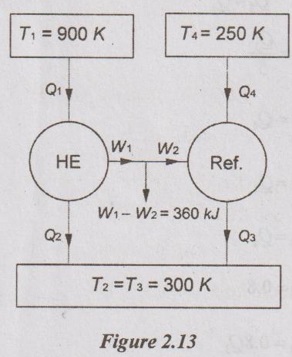
To Find: 

Q4 and Q2 + Q3

Solution:

Maximum efficiency of heat engine,

Heat transfer to refrigerator, Q4 = 4200.3 kJ   Ans.

We know that W2 = Q3 - Q4

840.06 = Q3 - 4200.3

⸫ Q3 = 840.06 + 4200.3 = 5040.36 kJ

⸫ Net heat transferred to the reservoir at 300 K,

= Q2 + Q3

= 599.94 + 5040.36 = 5640.3 kJ Ans.

Problem 2.6

A Carnot heat engine cycle works at maximum and minimum temperature of 1000°C and 40°C respectively. Calculate the thermal efficiency and work done if Q1= 1010 kJ.

Given data:

T1 = 1000°C = 1000 + 273 = 1273 K

T2 = 40°C = 40 + 273 = 313 K

Q1 = 1010 kJ

To find:

η and W

Solution:

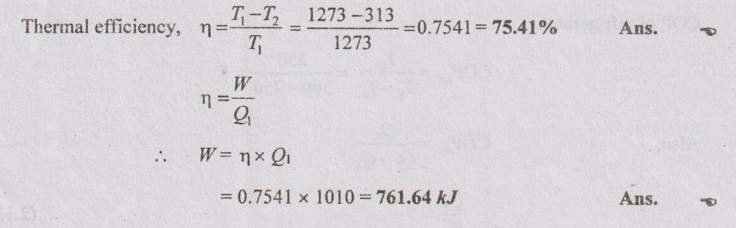
Problem 2.7

A Carnot heat engine receives heat from 600°C source. The efficiency of the engine is 59%. Find the amount of heat supplied and heat rejected per kW of work output.

Given data:

T1 = 600°C = 600 + 273 = 873 K

η = 59%

W = 1 kW

To find:

Q1 and Q2

Solution:

Problem 2.8

The temperature in a domestic refrigerator is to be maintained at -10°C. The ambient air temperature is 30°C. If the heat leaving through the refrigerator is 3 kW, determine the least power necessary to pump out this heat continuously.

Given data:

T4 = -10°C = -10 + 273 = 263 K

T3 = 30°C = 30 + 273 = 303 K 

Q3 = 3 kW

To find:

Power (W)

Solution:

A refrigerator removes heat at the same rate at which the heat leaks from it. For reversible engine, the condition of minimum power requirement,

Problem 2.9

Two-Carnot engines A and B are operated in series. The first one (A) receives heat at 870 K and rejects to a reservoir at temperature T. The second engine (B) receives the heat rejected by the first engine and in turn rejects to a heat reservoir at 300 K. Calculate the intermediate temperature T in °C between two heat engines for the following cases.

(a) The work output of the two engines is equal and

(b) The efficiencies of the two engines are equal.

Given data:

T1 = 870 K

T1 = 300 K

Case (i) WA = WB

Case (ii) ηA = ηB

To find:

Tin C for (i) WA = WB and (ii) case ηA = ηB

Solution:

Let, Q1 and Q2 are heat supplied to and rejected from HE-A respectively

Q3 and Q4 are heat supplied to and rejected from HE-B respectively

T is the intermediate temperature between HE-A and HE-B

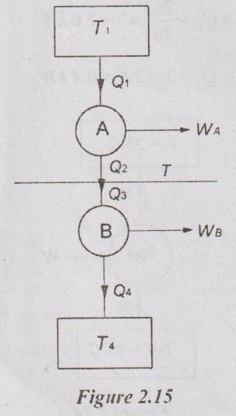
Case (i) WA = WB:

WA = Q1 - Q2 and WB = Q3 - Q4

We know that the work output of the two engines is equal.

⸫ Q1 – Q2 = Q3 – Q4

Q1 – Q2 = Q2 – Q4       [⸪ Q1 = Q2]

2 Q2 = Q1 + Q4

Problem 2.10

An office room which was heated by electric resistance heater consumes 1200 kWh of electrical energy in a winter month. Instead of this heater if the same office room is heated by a heat pump which is having 20% of COP of the ideal Carnot pump. The room temperature is 24°C while surrounding is at 0°C. If heat supplied from the surrounding by the heat pump is 0.65 kJ, determine COP and money saved per month. Assume the cost of electricity as Rs.1.75 per kWh.

Given data:

Power consumed by electric heater = 1200 kWh 

COP of HP = 20% of COP of ideal Carnot pump

T3 = 24°C = 24 + 273 = 297 K

T4 = 0°C = 0 + 273 = 273 K

Heat supplied by the HP, Q3 = 0.65 kW

Cost of electricity = Rs. 1.75/kWh

To find:

(i) COP of heat pump

(ii) Money saved per month.

Solution:

Electricity charge by using electric heater,

= 1200 × 1.75 = Rs. 2100 per month