Stress, Strain And Deformation Of Solids

 "Strength of materials" is a subject which deals with the detailed study about the effect of external forces acts on materials and ability of material to resist deformation.

Chapter 1:

STRESS, STRAIN AND DEFORMATION OF SOLIDS

• Rigid and deformable bodies

• Strength, stiffness and stability

• Hooke's law

• Stresses - tensile, compressive and shear

• Deformation of simple and compound bars under axial load

• Temperature stresses

• Elastic constants

• Stress on inclined plane

• Principal stresses and principal planes

• Mohr's circle of stresses

STRESS, STRAIN AND DEFORMATION OF SOLIDS

1. STRENGTH OF MATERIALS

"Strength of materials" is a subject which deals with the detailed study about the effect of external forces acts on materials and ability of material to resist deformation. The shape and size of various structures are designed by knowing the strength of materials.

2. STIFFNESS

The stiffness may be defined as an ability of a material to withstand high load without major deformation.

3. RIGID BODY

A rigid body consists of innumerable particles. If the distance between any two of its particles remains constant, it is known as solid body.

In actual practice, all the solid bodies are not perfectly rigid bodies. However, they are regarded as such, since all the solid bodies behave more or less like rigid bodies.

4. DEFORMABLE SOLIDS

A deformable solid body may be defined as a body which undergoes deformation due to application of external forces.

5. STRESS

When an external force acts on a body, it undergoes deformation and at the same time the body resists deformation. The magnitude of the resisting force is numerically equal to the applied force. This internal resisting force per unit area is called stress.

Mathematically, stress may be defined as the force per unit area.

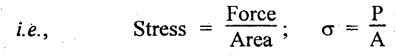
where,

σ - Stress, N/m2

P - Load or Force, N

A - Area, m2

6. STRAIN

When a body is subjected to an external force, there is some change in dimension of the body. Numerically, the strain is equal to the ratio of change in length to the original length of the body.

7. SIMPLE STRESS, COMPOUND STRESS

When a body is subjected to an external force in one direction, the stress developed in the body is called simple stress.

When a body is subjected to an external force in more than one direction, the stress developed in the body is called compound stress.

8. TYPES OF STRESSES

There are mainly three types of stresses. They are:

1. Tensile stress,

2. Compressive stress, and

3. Shear stress.

9. TYPES OF STRAINS

There are mainly three types of strains. They are:

1. Tensile strain,

2. Compressive strain, and

3. Shear strain.

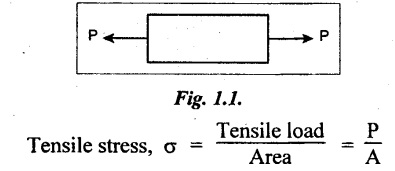
10. TENSILE STRESS, TENSILE STRAIN

When a member is subjected to equal and opposite axial pulls as shown in Fig.1.1, the length of the member is increased. The stress induced at any cross section of the member is called tensile stress.

The ratio of increase in length to the original length is known as Tensile strain.

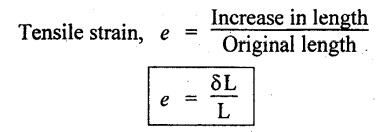
11. COMPRESSIVE STRESS, COMPRESSIVE STRAIN

When a member is subjected to equal and opposite axial pushes as shown in Fig.1.2, the length of the member is shortened. The stress induced at any cross section of the member is called compressive stress.

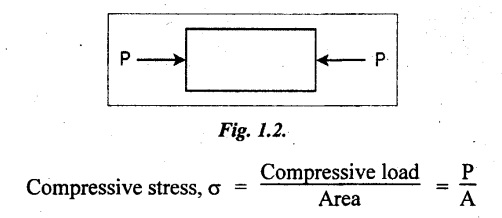
The ratio of decrease in length to the original length is known as compressive strain.

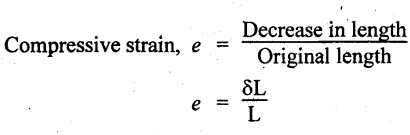
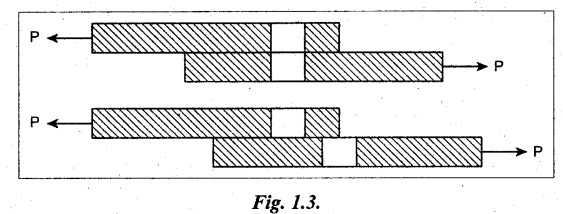
12. SHEAR STRESS, SHEAR STRAIN.

The two equal and opposite forces act tangentially on any cross-sectional plane of a body tending to slide one part of the body over the other part as shown in Fig.1.3. The stress induced in that section is called shear stress and the corresponding strain is known as shear strain.

13. VOLUMETRIC STRAIN

Volumetric strain is defined as the ratio of change in volume to the original volume of the body.

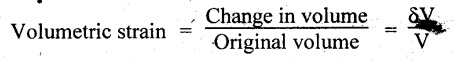
14. HOOKE'S LAW

It states that when a material is loaded, within its elastic limit, the stress is directly proportional to the strain.

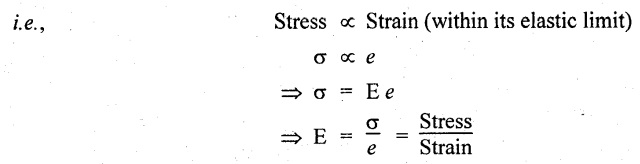
where E = Young's modulus or Modulus of elasticity

15. FACTOR OF SAFETY

It is defined as the ratio of ultimate tensile stress to the permissible stress (working stress).

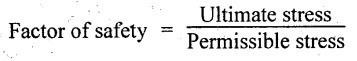
16. DEFORMATION OF A BODY DUE TO FORCE ACTING ON IT 

Consider a body subjected to a tensile stress.

We know that,

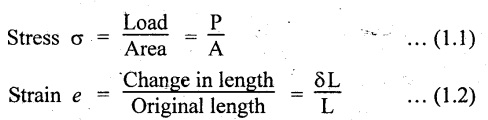
From Hooke's law,

Equating equations (1.2) and (1.3),

Units:

1. Stress, σ = N/mm2

2. Force or Pull = N

3. Length, (L) = mm

4. Diameter, (D) = mm

5. Modulus of Elasticity, (E) = N/mm2

6. Modulus of Rigidity, (G) = N/mm2

7. Bulk Modulus, (K) = N/mm2

8. 1 Pascal = 1 N/m2

17. FORMULAE USED

18. SOLVED PROBLEMS ON SIMPLE BARS UNDER AXIAL LOAD

Example 1.1 

A mild steel rod 2 m long and 3 cm diameter is subjected to an axial pull of 10 kN. If E for steel is 2 × 105 N/mm2. Find (a) Stress, (b) Strain, (c) Elongation of the rod.

Given:

L = 2 m = 2000 mm; D = 3 cm = 30 mm;

Axial pull, P = 10 kN = 10 × 103 N;

Modulus of Elasticity, E = 2 × 105 N/mm2.

To find: 

(a) Stress, (b) Strain, (c) Elongation.

Solution: We know that,

Results:

(a) Stress, σ = 14.14 N/mm2

(b) Strain, e = 7.07 × 10-5

(c) Elongation, δL = 0.141 mm.

Example 1.2: 

A rod of 2 m long is subjected to an axial pull of 30 kN. Find the minimum diameter of the rod if the permissible stress is limited to 200 × 106 N/m2. Also determine the elongation. Take E = 200 kN/mm2

Given:

L = 2 m 2 m = 2000 mm;

Axial pull, P = 30 kN 30 × 103 N:

Stress, σ = 200 × 106 N/m2

= 200 × 106 N / 106 mm2

= 200 N/mm2

E = 200 kN/mm2

= 200 × 103 N/mm2

= 2 × 105 N/mm2

To find: 

1. Minimum diameter (D), and

2. Elongation (δL).

Solution: 

We know that,

Result: 

1. Minimum diameter, D = 13.8 mm

2. Elongation, δL = 2 mm

Example 1.3: 

A hollow cylinder 1.5 m long has an outside diameter of 45 mm and inside diameter of 25 mm. If the cylinder is carrying a load of 20 kN, find the stress in the cylinder. Also find the deformation of the cylinder. Take E 100 GPa.

Given: 

L = 1.5 m = 1500 mm;

Ꭰ = 45 mm; d = 25 mm;

Load, P = 20 kN = 20 × 103 N.

Modulus of Elasticity, E = 100 GPa = 100 × 109 Pa

= 100 × 109 N/m2

= 100 × 109 N/106 mm2

= 100 × 103 N/mm2

To find: 

1. Stress, σ, 2. Deformation, δL.

Solution: 

We know that,

Result: 

1 Stress, = 1.81 N/mm2

2. Deformation, δL = 0.271 mm

Example 1.4: 

A hollow cylinder has an outside diameter of 25 cm carrying a axial load of 2.2 × 103 kN. Find the internal diameter of the cylinder if safe stress is 120 MN/m2.

Given:

D = 25 cm = 250 mm;

P = 2.2 × 103 kN = 2.2 × 106 N

= 120 MN/m2 = 120 × 106 N/m2

= 120 × 106 N/106 mm2

= 120 N/mm2

To find: 

Internal diameter, d.

Solution: 

We know that,

Result: Internal diameter, d = 197.8 mm

Example 1.5: 

A short hollow cast iron cylinder of external diameter 220 mm is to carry a compressive load of 600 kN. Determine the inner diameter of the cylinder, if the ultimate crushing stress for the material is 540 MN/m2. Use factor of safety of 6. 

Given:

External diameter, D = 220 mm

Load, P = 600 kN = 600 × 103 N

Ultimate stress = 540 MN/m2

= 540 × 106 N/m2

= 540 × 106 N/106 mm2

= 540 N/mm2

Factor of safety = 6

To find: 

Inner diameter, d

Solution: 

We know that,

We know that,

Result: 

Inner diameter, d = 199.77 mm

Example 1.6 

A cast iron column has internal diameter of 200 mm. What should be the minimum external diameter so that it may carry a load of 1.6 MN and safe stress is 90 N/mm2.

Given:

Internal diameter, d = 200 mm;

Load, P = 1.6 MN = 1.6 × 106 N

Stress, σ = 90 N/mm2.

To find:

External diameter, D.

Solution: 

We know that,

Result: 

External diameter, D = 250.2 mm

19. STRESSES IN BARS OF VARYING CROSS SECTIONS

Consider the following non-uniform cross sections of a member AB, BC and CD having cross sectional areas of A1, A2 and A3 with lengths of L1, L2 and L3 as shown in Fig.1.4.

20. SOLVED PROBLEMS ON VARYING CROSS SECTIONS

Example 1.7: 

A steel bar 900 mm long. Its two ends are 40 mm and 30 mm in diameter and the length of each rod is 200 mm. The middle portion of the bar is 15 mm in diameter and 500 mm long. If the bar is subjected an axial tensile load of 15 kN, determine (1) Stress in each section, (2) Total extension. [Take E 200 × 103 N/mm2]. 

Given: 

D1 = 40 mm; D2 = 15 mm; D3 = 30 mm; 

L1 = 200 mm; L2 = 500 mm; L3 = 200 mm.

P = 15 kN = 15 × 103 N; E = 200 × 103 N/mm2.

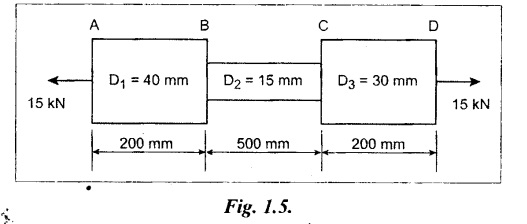
To find:

(1) Stress in each section, and

(2) Total extension.

Solution:

Stress in section AB:

Stress at section BC:

Stress at section CD:

We know that,

Result: 

σAB = 11.9 N/mm2;

σCD = 21.22 N/mm2;

σBC = 84.8 N/mm2

δL = 0.245 mm

Example 1.8: 

A round bar as shown in Fig. 1.6 is subjected to an axial tensile load of 100 kN. Determine the diameter (d) of the first part if the shear stress in the 290 GPa. first part is 100 MN/m2. Find also total elongation. Take E = 290 GPa

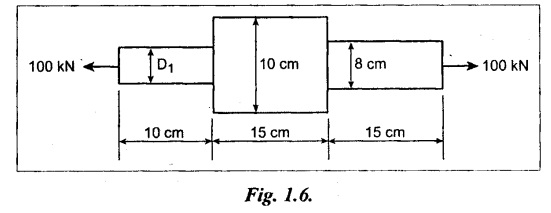
Given: 

P = 100 kN = 100 × 103 N;

L1 = 10 cm = 100 mm; L2 = 15 cm = 150 mm;

L3 = 15 cm = 150 mm; D2 = 10 cm = 100 mm;

D3 = 8 cm = 80 mm.

Stress at first portion, σ1 = 100 MN/m2 = 100 N/mm2

E = 290 GPa = 290 × 103 N/mm2

To find:

(1) Diameter of first portion, D1 and

(2) Total elongation, SL.

Solution: 

We know that,

Result:

Diameter of first portion, D1 = 35.68 mm

Total elongation, δL = 0.051 mm

Example 1.9: 

The bar shown in Fig. 1.7 is subjected to a tensile load of 150 kN. Find the diameter of the middle portion if the stress is limited to 160 N/mm2. Find also the length of the middle portion if the total elongation of the bar is 0.25 mm. Take E = 200 GN/m2.

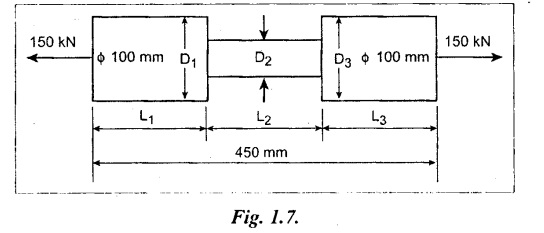
Given: 

P = 150 kN = 150 × 103 N; D1 = 100 mm;

Stress at middle portion, σ2 = 160 N/mm2;

D3 = 100 mm;

Total elongation, δL = 0.25 mm;

Young's modulus, E = 200 GN/m2

= 200 × 103 N/mm2

Total length, L = 450 mm

To find: 

(1) Diameter of the middle portion, D2, 

(2) Length of the middle portion, L2.

Solution: 

(1) Diameter of the middle portion D2:

Let,

Length of first portion = L1

Length of middle portion = L2

Length of last portion = L3

We know that,

Result: 

Diameter of the middle portion, D2 = 34.5 mm

Length of the middle portion, L2 = 293.3 mm

Example 1.10: 

A bar of steel is 0.7 m long. For the first 0.2 m it is 25 mm in diameter, for the next 0.3 m it is 20 mm in diameter and for remaining 0.2 m it is 15 mm in diameter. Find the change in length, if it is subjected to a tensile load of 1,00,000 N. The value of E is 0.210 MN/mm2.

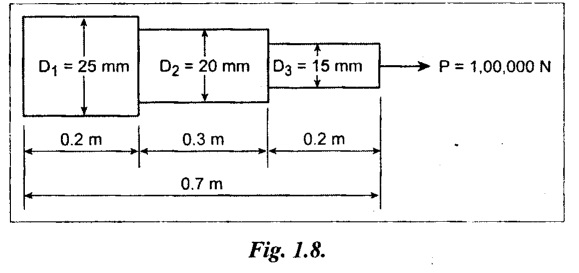
Given:

L = 0.7 m = 700 mm; L1 = 0.2 m = 200 mm;

L2 = 0.3 = 300 mm; L3 = 0.2 m = 200 mm

D1 = 25 mm; D2 = 20 mm; D3 = 15 mm

P = 1,00,000 N and

E = 0.210 MN/mm2 = 0.210 × 106 N/mm2

To find: 

Change in length (δL).

Solution: 

We know that,

Result: 

Change in length, δL = 1.187 mm

Example 1.11: 

An axial pull of 40 kN is acting on a bar consisting of three sections of length 300 mm, 250 mm, and 200 mm and of diameters 20 mm, 40 mm and 50 mm respectively. Find the stresses in each section and total extension of the bar. Take E = 2 × 105 N/mm2.

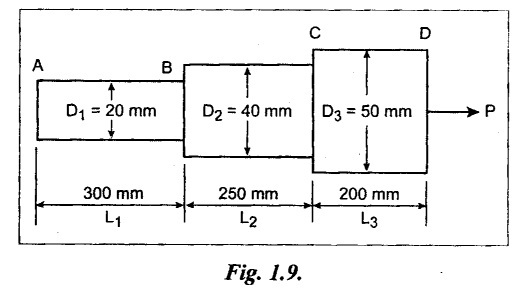
Given:

P = 40 kN = 40,000 N;

D1 = 20 mm;

D2 = 40 mm;

D3 = 50 mm

L1 = 300 mm;

L2 = 250 mm;

L3 = 200 mm

E = 2 × 105 N/mm2

To find: 

(1) Stresses in each section, and

(2) Total extension of the bar.

Solution: 

Stress at section AB:

Stress at section BC:

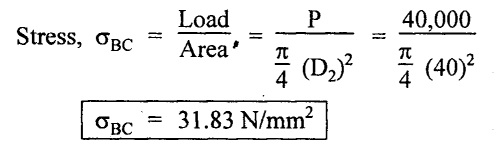
Stress at section CD:

We know that,

Result:

σAB = 127.38 N/mm2

σBC = 31.8 N/mm2

σCD = 20.38 N/mm2

δL = 0.25 mm

Example 1.12:

A bar of varying cross section consists of two sections of length 700 mm and 900 mm with cross sections 400 mm2 and 625 mm2. It is subjected to an axial pull of 100 kN. Take E 200 kN/mm2. Find the total elongation.

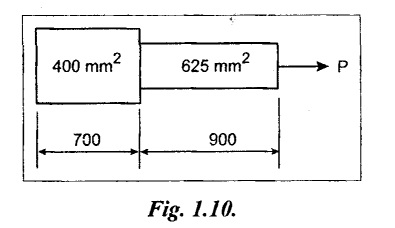
Given:

L1 = 700 mm; L2 = 900 mm

A1 = 400 mm2; A2 = 625 mm2

P = 100 kN = 100 × 103 N

E = 200 kN/mm2 = 200 × 103 N/mm2

To find: Total Elongation, δL

Solution: 

We know that.

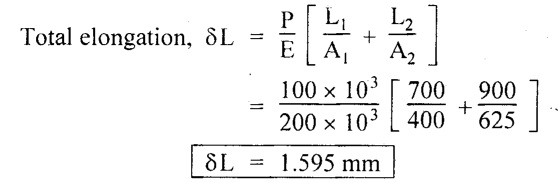
Result:

Change in length, SL = 1.595 mm