Solved Problems On Cantilever Beams

 solved problems on cantilever beams: Transverse Loading on Beams and Stresses in Beam - Strength of Materials

SOLVED PROBLEMS ON CANTILEVER BEAMS

Example 2.1: 

A cantilever beam of length 3m carries the point loads as shown in Fig. 2.9(a). Draw the shear force and bending moment diagrams for the cantilever beam.

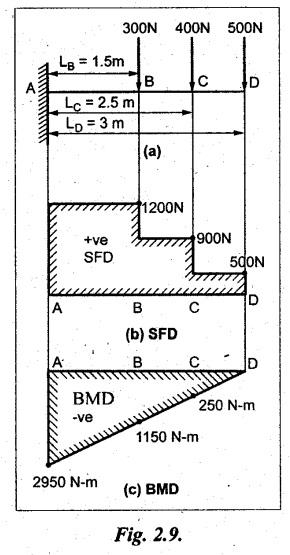
Given:

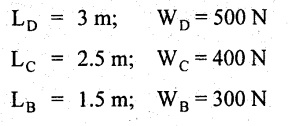
To draw: 

SFD and BMD

Solution:

SF calculation:

We know that, SF is the sum of forces on either left or right side of the section. Here we are considering from right side. The force acting downward and hence it is positive.

SF at D = + WD = + 500 N

SF between D and C remains constant and equal to +500 N. So, the forces are plotted above the base line and joined by the straight line.

SF at C = +WD + WC

= +500 + 400 = 900 N

SF between C and B remains constant and equal to +900 N

SF at B = +WD + WC + WB

= +500 + 400 + 300

= + 1200 N

SF between B and A remains constant and equal to +1200 N.

SF at A = + 1200 N        [since there is no load between A and B]

BM calculation

We know that,

BM at any section = Force × Distance from the corresponding section

Taking moments about the section D, C, B and A respectively from right side.

BM at D = WD × Distance from D

= -WD × 0 = 0

BM at C = -WD × Distance between D and C

= -WD × (LD - LC)

= - 500 × 0.5

= - 250 N-m

BM at B = - WD (LD - LB)- WC (LC – LB)

= - 500 × 1.5 - 400 × 1

= - 1150 N-m

BM at A = -WDLD - WC LC - WB LB

= - 500 × 3400 × 2.5 - 300 × 1.5 

= - 2950 N-m

The above result shows that the BM is zero at D and -ve value for all other points. So, the values are plotted below the base line AB and joined by inclined line.

Result:

The SF and BM values for all the points of the beam are plotted as shown in Fig.2.9(b) and (c) respectively.

Example 2.2: 

A cantilever beam of length 2m carries the point load of 1kN at its free end, and another load of 2 kN at a distance of Im from the free end. Draw the SF and BM diagrams for the cantilever beam.

Given:

LC = 2 m;

LB = 1 m;

WC = 1 kN 

WB = 2 kN

To draw: 

SFD and BMD

Solution: 

SF calculation:

SF at C = + 1 kN

SF at B = + 1 kN + 2 kN = 3 kN

SF at A = + 3 kN

BM calculation:

Taking moment from right side of the beam section considered.

BM at C = -WC × 0 = 0

BM at B = -WC (LC - LB) - WB × 0

= -1 × 1 – 2 × 0

= - 1 kN - m

BM at A = -WC × LC - WB × LB

= -1 × 2 – 2 × 1 = -4 kN - m

[Note: For details refer problem 2.1]

Result: 

SFD and BMD are represented by Fig.2.10(b) and (c) respectively.

Example 2.3:

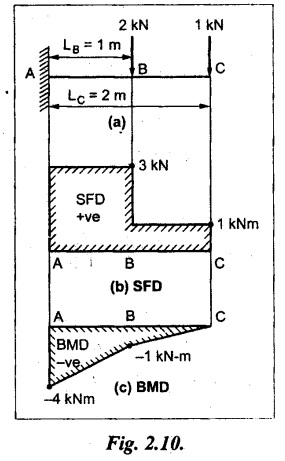
A cantilever of length 2 m carries a UDL of 3 kN/m. Draw the SF and BM diagrams.

Given: 

L = 2 m;

w = 3 kN/m

To draw: 

SFD and BMD

Solution:

SF calculation:

We know that, for UDL,

SF at any section of the beam is given by,

SF = Load × Length of the load spread over the section

SF = 3 kN/m x Length

SF at B = 3 × 0 = 0   [ ⸪ Distance is zero at B from right end.]

SF at A = 3 kN/m × 2 m = 6 kN

For UDL, the SFD is a sloped line. Draw the SFD as shown in Fig.2.11(b). 

BM calculation:

For UDL, the BM at any section of the beam is given by,

BM = Force × Distance

BM = Load × Length of the load spreaded × Distance

(i.e.,) BM at any section x from free end is given by,

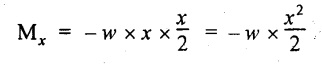
Taking moment from right side of the section considered,

BMD will be parabola for UDL. Draw the BMD as shown in Fig.2.11(c).

Result:

SFD and BMD are shown in Fig.2.11(b) and (c) respectively.

Example 2.4: 

A cantilever of length 3 m carries a UDL of 2 kN/m which run over a length of 2 m from the fixed end. Draw the SF and BM diagrams.

Given: 

L = 3 m;

w = 2 kN/m

l = 2 m.

To draw: 

SFD and BMD

Solution:

SF calculation:

SF at C = 0

SF at B = 0

SF at A = w × l = 2 kN/m × 2 m = 4 kN

Join all the values as shown in Fig.2.12(b).

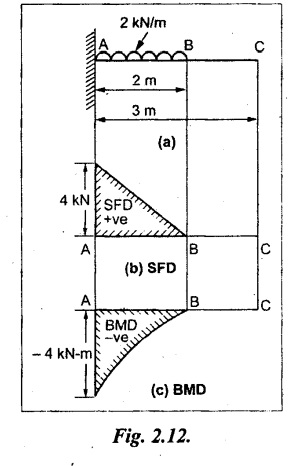
BM calculation:

BM at any section x from free end is given by

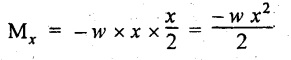
Taking moment from right side of the section considered.

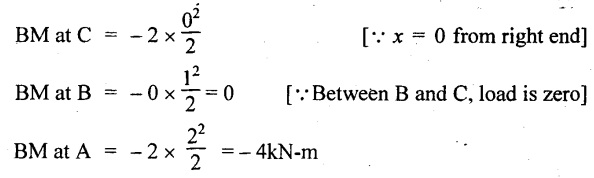
Join the values as shown in Fig.2.12(c).

Result: 

SFD and BMD are shown in Fig.2.12(b) and (c) respectively.

Example 2.5: 

A cantilever of length 3 m carries a UDL of 2 kN/m over a length of 2 m from the free end. Draw the SF and BM diagrams for the cantilever.

Given: 

L = 3 m;

w = 2 kN/m

l = 2 m

To draw: 

SFD and BMD

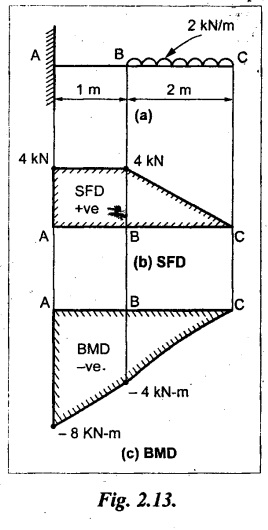
Solution:

SF calculation:

SF at C = 0

SF at B = 2 kN/m × 2 m

= 4 kN

SF at A= +4 kN

[Since, there is no load between A and B.]

The SF values between C and B are joined by a straight slopped line because of UDL and then between B and A by a straight horizontal line.

BM calculation:

BM at C = 0

Since the load is UDL, the BM values between C and B are joined by a parabolic curve. The point B and A are joined by a straight line because there is no load.

Résult:

SFD and BMD are shown in Fig.2.13(b) and (c) respectively.

Example 2.6: 

A cantilever of length 3 m carries a UDL of 3 kN/m over a whole length and a point load of 2 kN at the free end. Draw the SF and BM diagrams.

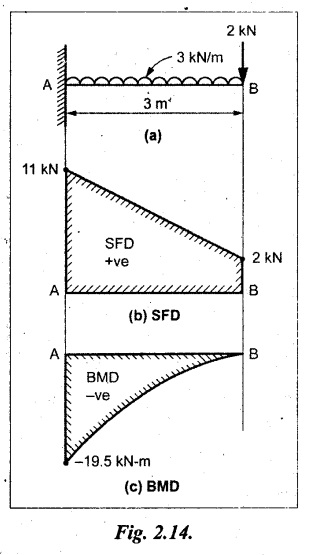
Given: 

As shown in Fig.2.14(a).

To draw: 

SFD and BMD.

Solution:

SF calculation:

SF at B = + 2 kN

SF at A = SF by point load + SF by UDL 

= +2 kN +3 kN/m × 3 m

SF at A = + 11 kN

Join all the S.F values as shown in Fig.2.14(b).

BM calculation:

BM at any section = BM by point load + BM by UDL

BM at B = 0

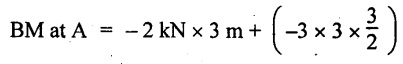
= -6 -13.5 = -19.5 kN-m

Draw the BM diagram as shown in Fig.2.14(b) and (c).

Result: SFD and BMD are shown in Fig.2.14(b) and (c) respectively.

Example 2: 

A cantilever of length 4 m carries a UDL of 3 kN/m run over the whole length and two point loads of 4 kN and 2.5 kN are placed Im and 2m respectively from the fixed end. Draw the SF and BM diagrams.

Given: 

As shown in Fig.2.15(a).

To draw: 

SFD and BMD

Solution:

SF calculation:

SF at D= 0

SF at C (without point load at C) = 3 kN/m × 2 m = 6 kN

Total SF at C = SF by point load

(i.e., 2.5 kN) + SF by UDL of length between C and D

(i.e., 2 m)         2.5 kN + 3 kN/m × 2 m = +8.5 kN

Similarly, SF at B (without point load at B).

= 2.5 kN +3 kN/m × 3 m = 11.5 kN

Total SF at B = +4 kN + 2.5 kN + 3 kN/m × 3 m 

= +15.5 kN

SF at A = 4 kN +2.5 kN + 3 kN/m × 4 = +18.5 kN

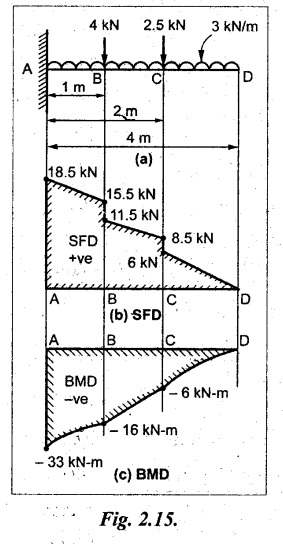
BM calculation:

BM at D = 0

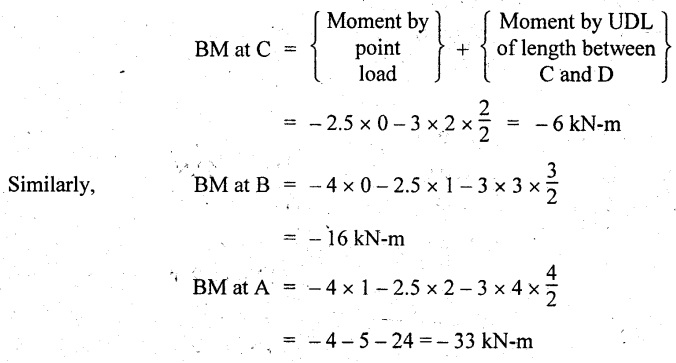
Draw the SF and BM diagrams as shown in Fig.2.15(b) & (c).

Result: 

SFD and BMD are shown in Fig.2.15(b) & (c) respectively.

Example 2.8:

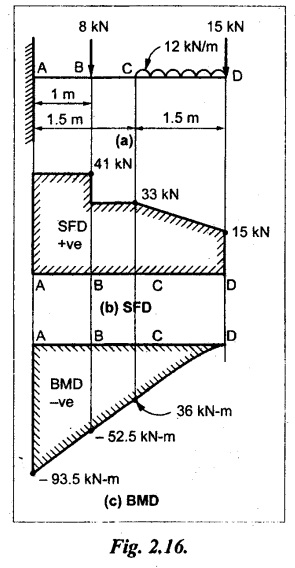
A cantilever of 3m long carries a UDL of 12 kN/m is spread over a length of 1.5m from the free end. It also carries a point load of 15 kN at free end and another point load of 8 kN at 1 m from the fixed end. Draw the SFD and BMD.

Given: 

As shown in Fig.2.16(a).

To draw: 

SFD and BMD

Solution:

SF calculation:

SF at D = +15 kN

SF at C = +15 kN + 12 kN/m × 1.5 m

= +15 + 18 = +33 kN

SF at B = +15 kN + 12 kN/m × 1.5 m + 8 kN

= +41 kN

SF at A = +41 kN

SF values between C and D are joined by a straight inclined line because of UDL acting at that section.

BM calculation:

BM at D = 0

BM at C = BM by point load at D + BM by UDL

The BM values between C and D are joined by parabolic curve. Since, the load is UDL. The BM values between BC and AB are joined by a straight inclined line. Thus, the BM is obtained.

Result: 

The BMD and SFD are shown in Fig.2.16(b) & (c) respectively.

Example 2.9: 

A cantilever beam of length 5m is loaded as shown in Fig.2.17(a). Draw the SF and BM diagrams.

Given: 

As showin Fig.2.17(a).

To draw: 

SFD and BMD

Solution:

SF calculation:

SF at D = 3 kN

SF at C = 3 + 2 = + 5 kN

SF at B (without point load)

= 3 kN + 2 kN + 3 kN/m × 1.5 m = + 9.5 kN

Total SF at B (i.e., considering point load)

3 kN + 2 kN + 3 kN/m × 1.5 + 2 kN = +11.5 kN 

SF at A = +11.5 kN

Draw the SF diagram as shown in Fig.2.17(b).

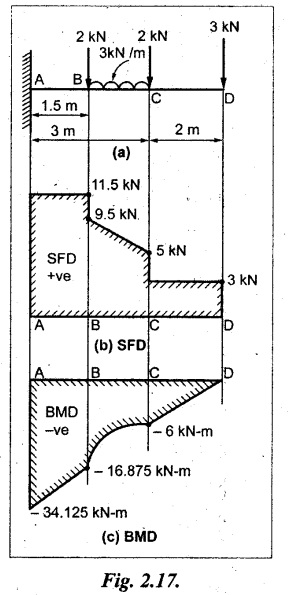
BM calculation:

BM at D = 0

The BM values between B and C are joined by parabolic curve because of UDL and all other values are joined by straight inclined lines as shown in Fig.2.17(c).

Result: 

BMD and SFD are shown in Fig.2.17(b) & (c) respectively.

Example 2.10: 

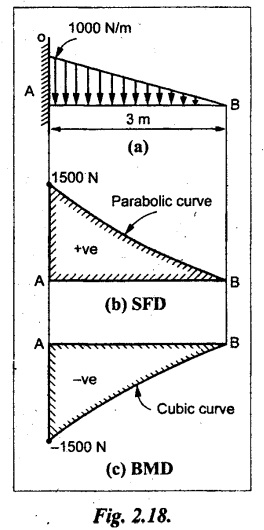
A cantilever beam 3m long carries a gradually varying load, zero at the free end to 1000 N/m at the fixed end. Draw the SF and BM diagrams for the beam.

Given: 

As shown in Fig.2.18(a).

To draw: 

SFD and BMD

Solution: 

SF calculation:

SF at B = 0.

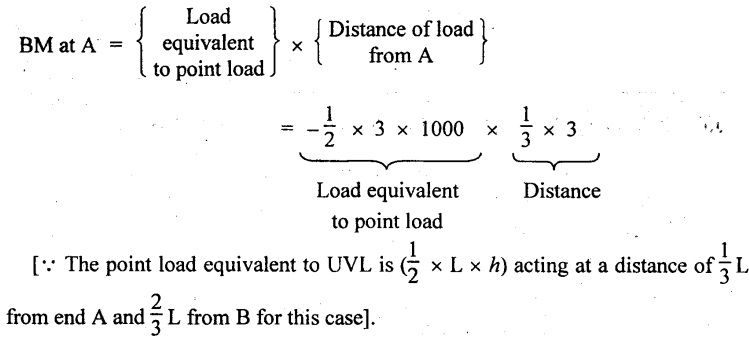
SF at A = Area of the triangle ABO

1/2 × 3 × 1000 = 1500 N

The SF is zero at B and increases parabolically to 1500 N at A.

BM calculation:

BM at B = 0

Draw the cubic curve between A and B as shown in Fig.2.18(c).

Result: 

The SFD and BMD are shown in Fig.2.18(b) & (c) respectively.