Stress, Strain and Deformation of Solids - Strength of Materials: Anna University Solved Problems
Stress, Strain and Deformation of Solids - Strength of Materials: University solved problems
UNIVERSITY SOLVED PROBLEMS
Example 1.44:
Determine the change in length, breadth and thickness of a steel bar 4 m lồng, 30 mm wide and 20 mm thick, when subjected to an axial pull of 120 kN in the direction of its length. Take E = 200 GPa and Poisson's ratio = 0.3.
Given:
Length, L = 4 m = 4000 mm;
Wide, b = 30 mm
Thickness, t = 20 mm;
Axial pull, P = 120 kN = 120 × 103 N
Young's Modulus, E = 200 GPa
= 200 × 109 Pa = 200 × 109 N/m2
= 200 × 103 N/mm2;
Poisson's ratio, 1/m = 0.3
To find:
1. Change in length, δL,
2. Change in breadth, δb,
3. Change in thickness, δt.
Solution:
We know that,

Result:
Change in length, δL = 4 mm
Change in breadth, δb = 9 × 10-3 mm
Change in thickness, δt = 6 × 10-3 mm
Example 1.45:
A bar of 30 mm diameter is subjected to a Pull of 60 kN. The measured extension on gauge length of 200 mm is 0.09 mm and the change in diameter is 0.0039. Calculate the Poisson's ratio and the value of the three moduli.
Given:
Diameter, d = 30 mm;
Pull, P = 60 kN = 60 × 103 N
Length, L = 200 mm;
Change in length, δL = 0.09 mm
Change in diameter, δd = 0.0039 mm
To find:
1. Poisson's ratio, 1/m,
2. Young's Modulus, E,
3. Bulk Modulus, K,
4. Modulus of Rigidity, G.
Solution:
We know that,

Substituting et, el values in equation (1),

We know that,

We know that,
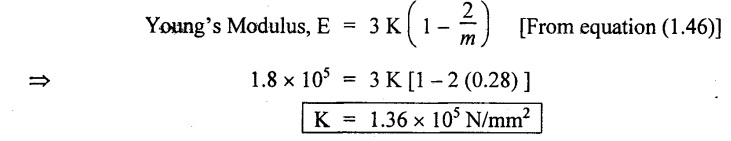
Result:
1. Poisson's ratio, 1/m = 0.28
2. Young's Modulus, E = 1.8 × 105 N/mm2
3. Modulus of Rigidity, G = 7.0 × 104 N/mm2
4. Bulk Modulus, K = 1.36 × 105 N/mm2
Example 1.46:
Find the young's modulus and Poisson's ratio of a metallic bar of length 300 mm, breadth 40 mm, depth 40 mm when the bar is subjected to an axial load of 40 kN. Decrease in length is 0.75 mm and the increase in breadth is 0.03 mm. Also find the modulus of rigidity of the bar.
Given:
Length, L = 300 mm
Breadth, b = 40 mm
Depth, t = 40 mm
Axial load, P = 40 kN = 40,000 N
Decrease in length, δL = 0.75 mm
Increase in breadth, δb = 0.03 mm
To find:
1. Young's Modulus, E,
2. Poisson's ratio, 1/m,
3. Modulus of Rigidity, G.
Solution:
We know that,

Substituting et, el, values in equation (1),

We know that,
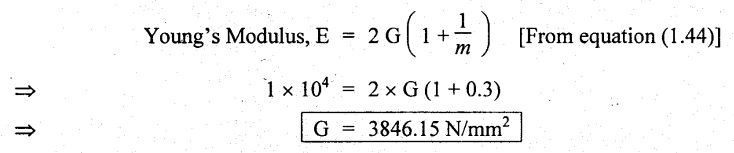
Result:
1. Young's Modulus, E = 1 × 104 N/mm2
2. Poisson's ratio, 1/m = 0.3
3. Modulus of Rigidity, G = 3846.15 N/mm2
Example 1.47:
When a metallic bar of length 25 cm, breadth 3 cm and depth 2 cm is subjected to an axial load of 240 kN. The decrease in length is 0.05 cm and increase in breadth is 0.002 cm. Determine the bulk modulus of the material.
Given:
Length, L = 25 cm = 250 mm
Breadth, b = 3 cm = 30 mm
Depth, t = 2 cm = 20 mm
Axial load, P = 240 kN = 240 × 103 N
Change in length, δL = 0.05 cm = 0.5 mm
Change in breadth, δb = 0.002 cm = 0.02 mm
To find:
(1) Bulk Modulus, K.
Solution:
We know that,

Result:
1. Bulk modulus, K = 1.96 × 105 N/mm2
Example 1.48:
For a given material, Young's Modulus is 1 × 105 N/mm2 and Modulus of rigidity is 4 × 10 N/mm2. Find the bulk modulus and lateral contraction of a round bar of 50 mm diameter and 2.5 m long, when length is increased 2.5 mm.
Given:
Young's Modulus, E = 1 × 105 N/mm2
Modulus Rigidity, G = 4 × 104 N/mm2
Diameter, d = 50 mm
Length, L = = 2.5 mm = 2500 mm
Change in length, δL = 2.5 mm
To find:
1. Bulk Modulus, K, and
2. Lateral contraction of round bar, δd.
Solution:
We know that,

We know that,

Substituting (1/m) and el values in equation (2),

We know that,
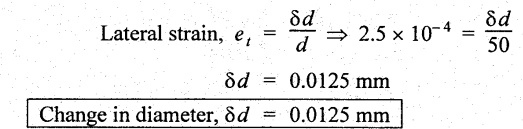
Substituting (1/m) values in equation (1),
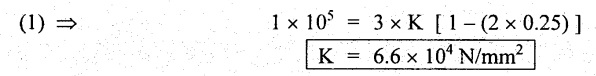
Result:
1. Bulk Modulus, K = = 6.6 × 104 N/mm2
2. Change in diameter, δd = 0.0125 mm
Example 1.49:
A bar of cross section 8 mm × 8 mm is subjected to an axial pull of 8000 N. The lateral dimension of the bar is found to be 7.996 × 7.996. If the modulus of rigidity of the material is 9.6 × 10 N/mm2. Determine the Poisson's ratio and modulus of elasticity.
Given:
Area, A = 8 mm × 8 mm = 64 mm
Axial pull, P = 8000 N
Lateral dimensions = 7.996 × 7.996 mm
Modulus of Rigidity, G = 9.6 × 104 N/mm2
To find:
(1) Poisson's ratio, 1/m,
(2) Modulus of Elasticity, E.
Solution:
We know that,

Substituting el and et values in equation (1),

Result:
Poisson's ratio, 1/m = 3.3
Young's Modulus, E = 8.3 × 105 N/mm2
Example 1.50:
Calculate the modulus of rigidity and bulk modulus of a cylindrical bar of diameter 25 mm and length 1.6 m. If the longitudinal strain in a bar during tensile stress is four times the lateral strain. Determine the change in volume, when the bar is subjected to a hydrostatic pressure of 100 N/mm2. Take E = 1 × 105 N/mm2.
Given:
Diameter, d = 25 mm
Length, L = 1.6 m = 1600 mm
Longitudinal strain = 4 × Lateral strain
el = 4et
Stress, σ = 100 N/mm2
Young's modulus, E = 1 × 105 N/mm2
To find:
1. Modulus of Rigidity, G,
2. Bulk Modulus, K,
3. Change in volume, dV.
Solution:
We know that,

We know that,

Result:
1. Modulus of Rigidity, G = 4 × 104 N/mm2
2. Bulk modulus, K = 0.66 × 105 N/mm2
3. Change in volume, dV = 1178 mm3ANNA UNIVERSITY SOLVED PROBLEMS
Example 1.51:
A 20 mm diameter bar was subjected to an axial pull of 40 kN and change in diameter was found to be 0.003822 mm. Find the Poisson's ratio, modulus of elasticity and Bulk modulus if the shear modulus of the material of the bar is 76.923 GPa.
Given:
Diameter d = 20 mm;
Axial pull P = 40 kN = 40 × 103 N
Change in diameter δd = 0.003822 mm
Shear modulus or Modulus of Rigidity G = 76.923 GPa
= 76.923 × 103 N/mm2
To find:
1. Poisson's ratio (1/m),
2. Modulus of Elasticity (E), and
3. Bulk Modulus (K).
Solution:
We know that,

Substituting et value in equation (1),

We know that,

Substituting m value in equation (3),
(3) ⇒ 3.35 (E) = 6.7 × 105
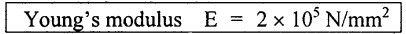
We know that,
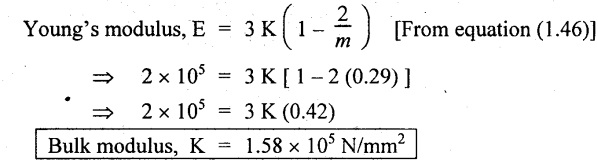
Result:
1. Poisson's ratio (1/m) = 0.29
2. Modulus of elasticity (E) = 2 × 105 N/mm2
3. Bulk modulus (K) = 1.58 × 105 N/mm2
Example 1.52:
The Young's modulus of a material is 210 kN/mm2 and its modulus of rigidity is 75 kN/mm2. Determine the bulk modulus.
Given:
Young's modulus, E = 210 kN/mm2
= 210 × 103 N/mm2
Modulus of rigidity, G = 75 kN/mm2
To find:
Bulk modulus, K
Solution:
We know that,
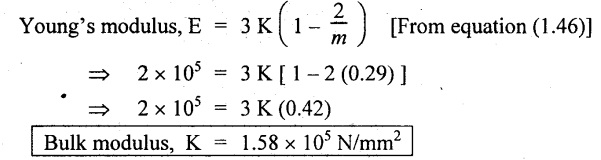
Result:
Bulk modulus K 3.5 × 105 N/mm2
Example 1.53:
A circular rod is subjected to a pull of 60 kN. The measured extension on a gauge length of 180 mm is 0.09 mm and the change in diameter is 0.00276 mm. Calculate the Poisson's ratio and the value of other moduli if Young's modulus = 200 kN/mm2.
Given:
Axial pull, P = 60 kN = 60 × 103 N;
Length, L = 180 mm
Change in length, δL = 0.09 mm
Change in diameter, δd = 0.00276 mm
Young's modulus, E = 200 kN/mm2
= 200 × 103 N/mm2
To find:
1. Poisson's ratio (1/m),
2. Modulus of rigidity or Shear modulus
[G or C or N]
3. Bulk modulus (K).
Solution:
We know that,
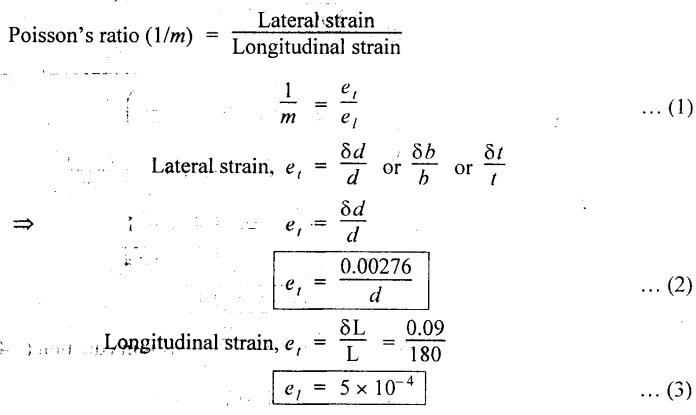
We know that,

We know that,

Substituting d value in equation (2),
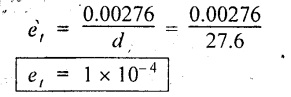
Substituting et and el values in equation (1),

Result:
1. Poisson's ratio, 1/m = 0.2
2. Modulus of rigidity, G = 8.3 × 104 N/mm2
3. Bulk modulus, K = 1.1 × 105 N/mm2
Example 1.54:
Find the value of P and the change in length of each component and the total change in length of the bar shown in Fig. 1.34.
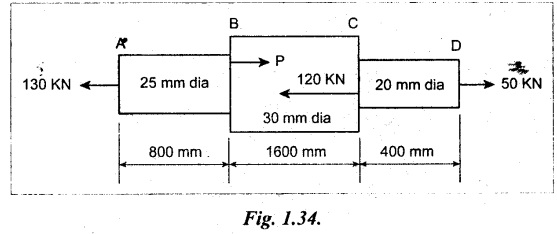
Given:

Length of section CD, L3 = 400 mm
Young's modulus, E = 200 kN/mm2
= 200 × 103 N/mm2
E = 2 × 105 N/mm2
To find:
1. Force P.
2. Change in length of each component.
3. Total change in length.
Solution:
We know that,
Forces acting towards right = Forces acting towards left
⇒ P + 50 = 130 + 120
⇒ P = 200 KN

Consider part AB: Take, tensile force (T) is positive. Compressive force (C) is negative.
Right hand side force = P (T) – 120 kN (C) + 50 kN (T)
་= 200 kN (T) – 120 kN (C) + 50 kN (T)
= 130 kN (T)
Left hand side force = 130 kN (T)
So, load on part AB is 130 kN (T) = 130 × 103 N (T)
Consider part BC:
Right hand side force = - 120 kN (C) + 50 kN (T)
= - 70 kN (C)
Left hand side force = 130 kN (T) – P (C)
= 130 kN (T) - 200 kN (C)
= 70 kN (C)
So, load on part BC is 70 kN (C) = 70 × 103 N (C)
Consider part CD:
Right hand side force = 50 kN (T)
Left hand side force = 130 kN (T) – P (C) + 120 kN (T)
= 130 kN (T) – 200 kN (C) + 120 kN (T)
= 50 kN (T)
So,
load on part CD is 50 kN (T) = 50 × 103 N (T)
We know that,

Result:
1. Force P = 200 KN
2. Change in length of part AB, δL1 = 1.06 mm
Change in length of part BC, δL2 = 0.792 mm
Change in length of part CD, δL3 = 0.317 mm
3. Total change in length, δL = 2.169 mm
Example 1.55:
A bar of 30 mm x 30 mm x 250 mm long was subjected to a pull of 90 kN in the direction of its length. Then extension of the bar was found to be 0.125 mm, while the decrease in each lateral dimension was found to be 0.00375 mm. Find the Young's modulus, Poisson's ratio and rigidity modulus of the bar.
Given:
Length L = 250 mm
Breadth b = 30 mm
Depth d = 30 mm
Axial load P = 90 kN = 90 × 103 N
Increase in length δL = 0.125 mm
Decrease in length δb = 0.00375 mm
To find:
1. Young's modulus, E.
2. Poisson's ratio(1/m).
3. Rigidity modulus (G).
Solution:
We know that,

We know that,

Result:
1. Young's modulus E = 2 × 105 N/mm2
2. Poisson's ratio (1/m) = 0.25
3. Modulus of rigidity G = 80 × 103 N/mm2
Example 1.56:
A steel plate 300 mm long, 60 mm wide and 30 mm deep is acted upon by the forces shown in Fig. 1.35. Determine the change in volume. Take E = 200 kN/mm2 and Poisson's ratio = 0.3.
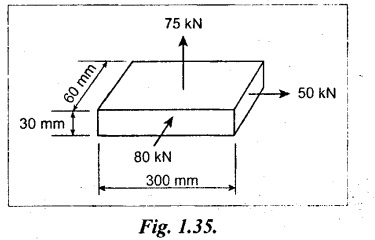
Given:
Length x = 300 mm
Width y = 60 mm
Depth z = 30 mm
Load in the direction of x = 50 kN = 50 × 103 N
Load in the direction of y = - 80 kN = -80 × 103 N
[ ⸪ Compressive load]
Load in the direction of z = 75 kN = 75 × 103 N
Young's modulus E = 200 kN/mm2 = 2 × 105 N/mm2
Poisson's ratio (1/m) = 0.3
To find:
Change in volume (dV).
Solution:

Result:
Change in volume dV = 24.89 mm3
Example 1.57:
The composite bar shown in Fig.1.36 is rigidly fixed at the ends. An axial pull of P = 15 kN is applied at B at 20°C. Find the stresses in each material at 80 °C.
Take
αs = 11 × 106/°C; αa = 24 × 10-6/°C
Es = 210 kN/mm2; Ea = 70 kN/mm2
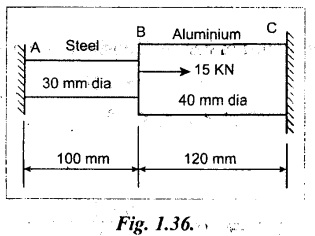
Given:
Diameter of steel bar, Ds = 30 mm
Diameter of aluminium bar, Da = 40 mm
Length of steel bar, Ls = 100 mm
Length of aluminium bar, La = 120 mm
Axial pull at 20°C, P = 15 kN = 15 × 103 N
Rise in temperature, T = 80°C – 20°C
T = 60°C
Coefficient of linear expansion for steel, αs = 11 × 10-6 / °C
Coefficient of linear expansion for aluminium,
αa = 24 × 10-6 /°C
Young's modulus for steel, Es = 210 kN/mm2 = 210 × 103 N/mm2
Es = 2.1 × 105 N/mm2
Young's modulus for aluminium, Ea = 70 kN/mm2 = 70 × 103 N/mm2
Ea = 0.7 × 105 N/mm2
To find:
1. Stress in steel at 80°C.
2. Stress in aluminium at 80°C.
Solution:
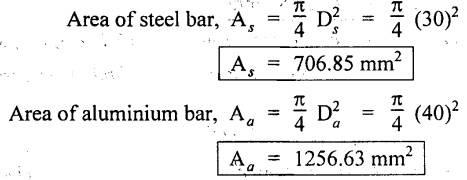
At 20°C:
Compressive load on aluminium bar = Tensile load on steel

At 60°C:
Compressive load on aluminium bar = Tensile load on steel

We know that,
Actual expansion of steel = Actual expansion of aluminium

From equation (4), we know that,

Result:
1. Stress in steel at 80°C = 95.43 N/mm2
2. Stress in aluminium at 80°C = 53.63 N/mm2
Example 1.58:
A rod of length 1 m and diameter 20 mm is subjected to a tensile load of 20 kN. The increase in length of the rod is 0.30 mm and decrease in diameter is 0.0018 mm. Calculate the Poisson's ratio and three moduli.
Given:
Rod length, L = 1 m = 1000 mm
Diameter, d = 20 mm
Load, P = 20 kN = 20 × 103 N
Change in length, δL = 0.30 mm
Change in diameter, δd = 0.0018 mm
To find:
1. Poisson's ratio (1/m).
2. Young's modulus (E).
3. Bulk modulus (K).
4. Modulus of rigidity (G).
Solution:
We know that,

We know that,

We know that,

We know that,

Result:
1. Poisson's ratio, 1/m = 0.3
2. Young's modulus, E = 2.12 × 105 N/mm2
3. Modulus of rigidity, G = 8.15 × 104 N/mm2
4. Bulk modulus, K = 1.76 × 105 N/mm2
Example 1.59:
A steel tube 30 mm externa! diameter and 25 mm internal diameter encloses a gun metal rod 20mm diameter to which it is rigidly joined at each end. The temperature of the whole assembly is raised to 150°C. Find the intensity of stress in the rod when the common temperature has fallen to 20°C. The value of the Young's modulus for steel and gun metal are 2.1 × 105 N/mm2 and 1 × 105 N/mm2 respectively. The coefficient of linear expansion for steel is 12 × 10-6/°C and for gun metal is 20 × 10-6/°C.
Given:
External diameter of steel tube, Ds = 30 mm
Internal diameter of steel tube, ds = 25 mm
Diameter of gun metal, Dg = 20 mm
Fall in temperature, T = 150°C - 20
T = 130°C
Young's modulus for steel, Es = 2.1 × 105 N/mm2
Young's modulus for gun metal, Εg = 1 × 105 N/mm2
Coefficient for linear expansion for steel, αs = 12 × 10-6 /°C
Coefficient for linear expansion for metal gun αg = 20 × 10-6 /°C
To find:
1. Stress in the steel.
2. Stress in the gun metal.
Solution:

Coefficient of linear expansion of gun metal is more than that of steel. So, gun metal will be subjected to compressive stress whereas steel will be subjected to tensile stress.
We know that,
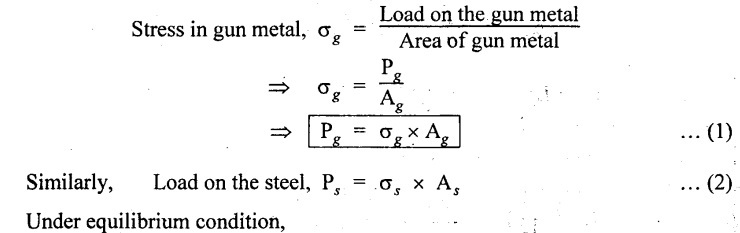
Under equilibrium condition,
Compression in the gun metal is equal to tension in the steel tube.
i.e., Load on the gun metal = Load on the steel tube

We know that,

We know that,
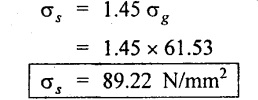
Result:
1. Stress in the steel tube σs = 89.22 N/mm2
2. Stress in the gun metal σg = 61.53 N/mm2
Example 1.60 :
A metallic bar 250 mm × 100 mm × 50 mm is loaded as shown in Fig.1.37. Find the change in volume. Take E = 2 × 105N/mm2 and Poisson's ratio = 0.25. Also find the change that would be made in the 4 MN load, in order that there should be no change in the volume of the bar.
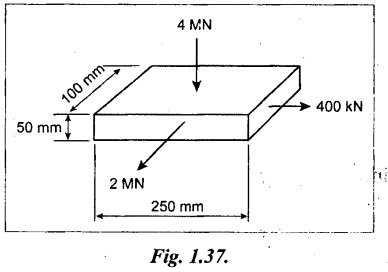
Given:
Dimensions of bar = 250 mm × 100 mm × 50 mm
Length x = 250 mm
Width y = 100 mm
Depth z = 50 mm
Load in the direction of x = 400 KN
= 400 × 103 N (tensile)
Load in the direction of y = 2 MN = 2 × 106 N (tensile)
Load in the direction of z = 4 MN = -4 × 106 N
[ ⸪ Compressive load]
Young's modulus E = 2 × 105 N/mm2
Poisson's ratio (1/m) = 0.25
To find:
1. Change in volume (ɗV).
2. Change in load.
Solution: Case (i):

We know that,

Case (ii): Change in the 4 MN load - when there is no change in volume of bar.
We know that,
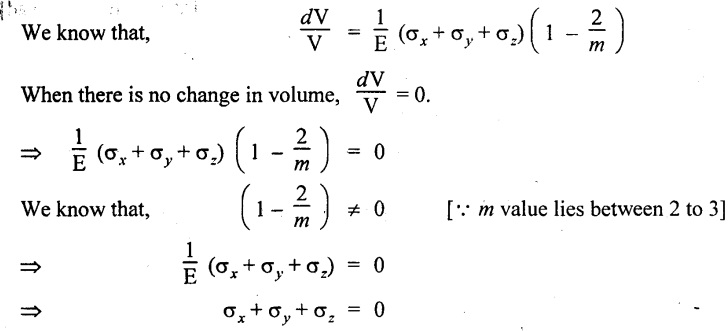
The stresses σx and σy will not be changed. The stress corresponding to the load 4 MN i.e., stress in z direction will be changed.

4 MN load is already acting. So additional load is to be added
= 6 MN - 4 MN
= 2 MN [Compressive load]
Result:
1. Change in volume, dV = 250 mm3
2. Additional load in z direction = 2 MN [Compressive load]
Example 1.61:
Derive a relation for change in length of a bar of uniformly tapering circular section subjected to an axial tensile load W.
Ans: Refer Section 1.1.23, Equation No. (1.10).
Example 1.62:
A reinforced concrete column 500 mm × 500 mm in section is reinforced with 4 steel bars of 25 mm diameter, one in each corner, the column is carrying a load of 1000 kN. Find the stresses in the concrete and steel bars. Take
E for steel = 210 × 103 N/mm2 and
E for concrete = 14 × 103 N/mm2
Given:
Area of column = 500 mm × 500 mm
= 0.25 × 106 mm2
Diameter of steel bar, ds = 25 mm
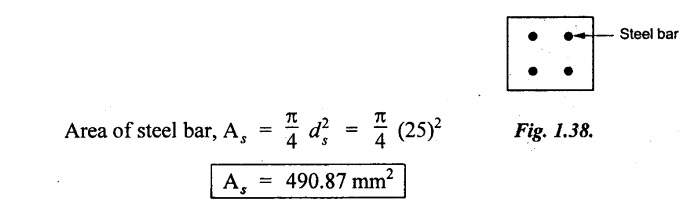
For four steel bar, As = 4 × 490.87

To find:
1. Stress in concrete, σc.
2. Stress in steel bars, σs.
Solution:
We know that,
Total load, P = Load on steel bar + Load on concrete

We know that,
Change in length of concrete = Change in length of steel bar

Substituting Ps value in equation (1),

Result:
1. Stress in steel bar σs = 53.47 N/mm2
2. Stress in concrete σc = 3.60 N/mm2
No comments:
Post a Comment