Consider a bar of length L, tapering from diameter D2 to D1 and subjected to axial load P as shown in Fig.1.16.
EXTENSION OF UNIFORMLY TAPERING ROD

Consider a bar of length L, tapering from diameter D2 to D1 and subjected to axial load P as shown in Fig.1.16.
We know that,

We know that,

Extension of the small elemental length dx
= Strain × dx = e × dx
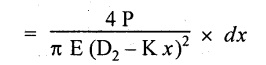
For total extension,

Substituting K value,

Note: For uniformly tapering rectangular plate
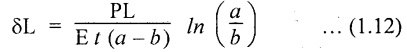
24. SOLVED PROBLEMS
Example 1.18:
A steel rod circular in section, tapers from 3 cm diameter to 1.5 cm diameter in a length of 60 cm. Find how much its length will increase under a tensile force 22 kN. Take E = 2 × 105 N/mm2.
Given:
Smaller diameter, D1 = 1.5 cm = 15 mm
Bigger diameter, D2 = 3 cm = 30 mm
Length, L = 60 cm = 600 mm;
Force, P = 22 kN = 22000 N
E = 2 × 105 N/mm2.
To find:
Total Extension, δL.
Solution:
We know that,

Example 1.19:
A rod which tapers uniformly from 40 mm diameter to 20 mm diameter in length of 400 mm is subjected to an axial load of 5000 N. Find the modulus of elasticity for a rod if extension of the rod is 0.015 mm.
Given:
D1 = 20 mm; D2 = 40 mm; L = 400 mm;
Force, P = 5000 N; Extension, δL = 0.015 mm.
To find:
Modulus of Elasticity (E).
Solution:
We know that,
Total extension for tapered rod is,

Result:
Modulus of Elasticity, E = 2.12 × 105 N/mm2
Example 1.20:
A circular rod 2.5 m long, tapers uniformly from 25 mm diameter to 12 mm diameter. Determine the extension of the rod under a pull of 30 kN. Assume modulus of elasticity of the rod is 200 kN/mm2.
Given:
L = 2.5 m = 2500 mm;
Bigger diameter, D2 = 25 mm;
Smaller diameter, D1 = 12 mm;
Force, P = 30 kN = 30 × 103 N;
E = 200 kN/mm2 = 200 × 103 N/mm2.
To find:
Extension of the rod.
Solution:
For tapered rod,

Result:
Change in length, δL = 1.59 mm
Example 1.21:
A steel flat plate ab of 1 cm thickness tapers uniformly from 10 cm to 5 cm width in a length of 40 cm. Determine the elongation of the plate, if an axial tensile force of 5000 N acts on it. Take E = 2 × 105 N/mm2.
Given:
Thickness, t = 1 cm = 10 mm;
Width at bigger end, a = 10 cm = 100 mm;
Width at smaller end, b = 5 cm = = 50 mm;
Length, L = 40 cm = 400 mm;
Axial load, P = 5000 N; E = 2 × 105 N/mm2
To find:
Elongation of the plate.
Solution:
We know that,

Result:
Elongation, δL = 0.138 mm
25. STRESSES IN COMPOSITE BARS
A composite member is composed of two or more different materials which are joined together. So that the system is elongated or compressed as a single unit. In such case, the following two governing principles are to be followed.
(1) Elongation or contraction in each bar is equal. So, the strains induced in those bars are also equal.
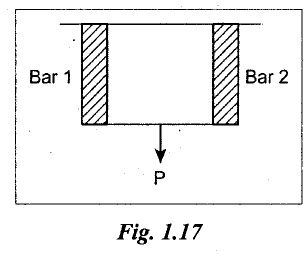
Change in length of bar (1) = Change in length of bar (2)

(2) The sum of loads carried by individual materials of a composite member is equal to the total load applied on the member.
26. SOLVED PROBLEMS ON COMPOUND BARS
Example 1.22:
A compound bar of length 500 mm consists of a strip of aluminium 40 mm wide × 15 mm thick and a strip of steel 40 mm wide × 10 mm thick rigidly joined at ends. If the bar is subjected to a load of 50 kN, find the stress developed in each material and the extension of the bar. Take modulus of elasticity of aluminium and steel as 1.1 × 105 N/mm2 and 2.1 × 105 N/mm2.
Given:
Length, L = 500 mm
Area of aluminium, Aa = 40 × 15 = 600 mm2
Area of steel, As = 40 × 10 = 400 mm2
Load, P = 50 kN = 50,000 N
Modulus of Elasticity for Aluminium, Ea
= 1.1 × 105 N/mm2
Modulus of Elasticity for steel, Es
= 2.1 × 105 N/mm2
To find:
1. Stress developed in each material, and
2. Extension in each material.

Solution:
We know that,
Total load, P = Pa + Ps = 50,000 = Pa + Ps
[From equation (1.14)]
⇒ 50,000 = Pa + Ps
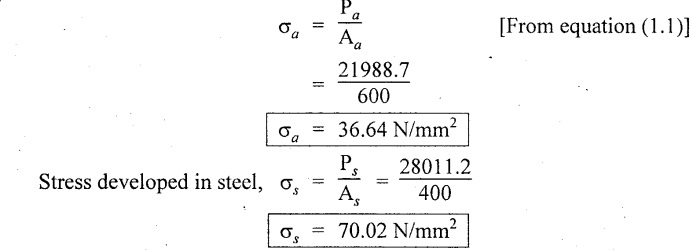
Change in length of aluminium = Change in length of steel

Substituting Pa value in equation (A),

Stress developed in aluminium,
Change in length of aluminium = Change in length of steel
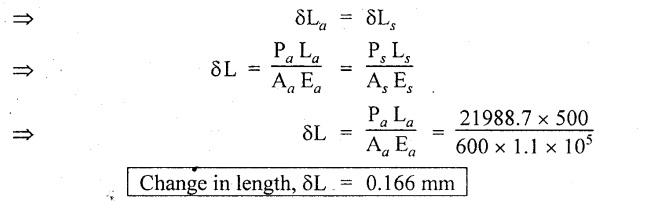
Result:
1. Stress developed in aluminium, σa = 36.64 N/mm2
Stress developed in steel, σs = 70.02 N/mm2
2. Extension in each material
i.e., change in length, δL = 0.166 mm
Example 1.23:
A short steel tube of external diameter 70 mm and internal diameter 40 mm is surrounded by a brass tube of same length and having external diameter 90 mm and internal diameter 80 mm. The tubes are rigidly fixed and an axial load of 20 kN is placed on the tubes. Find the load carried in each tube and shortening of each tube. Take L 30 cm, modulus of elasticity of steel is 2.1 × 105 N/mm2 and modulus of Elasticity of brass is 1.1 × 105 N/mm2.
Given:
Steel Tube:
External diameter = 70 mm;
Internal diameter = 40 mm;
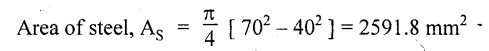
Brass Tube:
Internal diameter = 80 mm
External diameter = 90 mm

Load, P = 20 kN = 20,000 N
Length, L = 30 cm = 300 mm
Es = 2.1 × 105 N/mm2
Eb = 1.1 × 105 N/mm2
To find:
(1) Load carried in each tube,
(2) Shortening of each tube.
Solution:
We know that,
Total load, P = Load on steel + Load on brass

Change in length of steel = Change in length of brass

Lengths of the two rods are same.
So, Ls = Lb = L = 300 mm
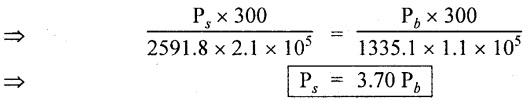
Substituting Ps value in equation (A),

From equation (B),
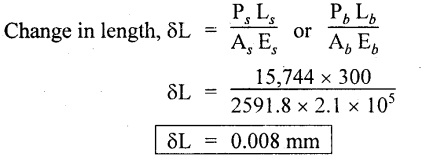
Result:
1. Load on steel, Ps = 15,744 N
Load on brass, Pb = 4255.3 N
2. Shortening of tube, δL = 0.008 mm
Example 1.24:
A steel rod of 25 mm diameter is enclosed centrally in a copper hollow tube of external diameter 40 mm and internal diameter 30 mm. The composite bar is then subjected to an axial pull of 4500 N. If the length of each bar is equal to 130 mm, determine:
(1) The stress in the rod and tube;
(2) Load carried by each bar.
Take Es = 2.1 × 105 N/mm2, Ec = 1.1 × 105 N/mm2.
Given:
Steel rod:
Diameter = 25 mm
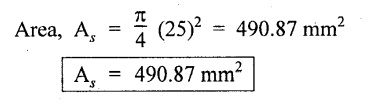
Copper hollow tube:
External diameter, D = 40 mm
Internal diameter, d = 30 mm
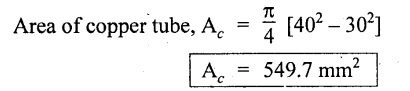
P = 4500 N; Length, L = 130 mm
Es = 2.1 × 105 N/mm2
Ec = 1.1 × 105 N/mm2
To find:
1. Stress in the steel rod and copper tube,
2. Load carried by rod and tube.
Solution:
We know that,
Total load, P = Load on steel rod + Load on copper tube

We know that,
Change in length of steel rod = Change in length of copper tube

Lengths of two rods are equal.

Substituting Ps value in equation (A),

Result:
Pc = 1666.6 N; Ps = 2833.22 N
σc = 3.03 N/mm2; σs = 5.77 N/mm2
Example 1.25:
A reinforced concrete column 50 cm × 50 cm in section is reinforced with 4 steel bars of 2.5 cm diameter, one in each corner. The column is carrying a load of 2 MN. Find the stresses in the concrete and steel bars.
Take,
Modulus of Elasticity for steel Es = 2.1 x 105 N/mm2
Modulus of Elasticity for concrete EC = 1.4 × 104 N/mm2
Given:
Concrete column dimensions = 50 cm × 50 cm
= 500 mm × 500 mm
Diameter of steel bar, Ds = 2.5 cm = 25 mm
Load, P = 2 MN = 2 × 106 N
Es = 2.1 × 105 N/mm2
EC = 1.4 × 104 N/mm2
To find:
Stresses in the concrete and steel bars.
Solution:
Area of column = 500 mm × 500 mm
= 25 × 104 mm2
= 2500 cm2

⸫ Area of concrete = Area of column - Area of steel
= 250000 - 1963.4

We know that,
Total load, P = Load on steel bar + Load on concrete

We know that,
Change in length of steel bar = Change in length of concrete

The length of steel bar and concrete are equal.
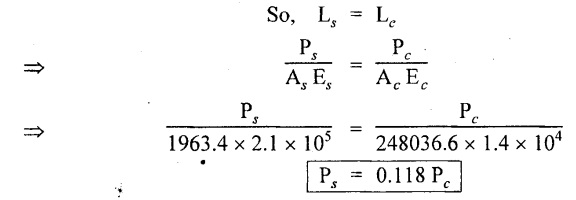
Substituting in (A),

Result:
Stress on steel bar, σs = 106.96 N/mm2
Stress on concrete, σc = 7.18 N/mm2
Example 1.26:
A mild steel rod of 20 mm diameter and 300 mm long is enclosed centrally inside a hollow copper tube of external diameter 30 mm and internal diameter 25 mm. The ends of the rod and tube are brazed together and the composite bar is subjected to an axial pull of 50 kN. If E for steel and copper are 200 GPa and 100 GPa respectively. Find the stresses developed in rod and tube.
Given:
Steel rod diameter = 20 mm
Area of steel, As = π/4(20)2 = 314.16 mm2
Hollow copper tube:
External diameter, D = 30 mm
Internal diameter, d = 256 mm
Area of copper tube = π/4 (302 - 252)

Load, P = 50 kN = 50,000 N
Es = 200 GPa = 200 × 109 Pa
= 200 × 109 N/m2
= 200 × 103 N/mm2
= 2 × 105 N/mm2
Ec = 100 GPa = 100 × 109 Pa
= 100 × 109 N/m2
= 100 × 103 N/mm2 = 1 × 105 N/mm2
To find:
Stresses developed in rod and tube.
Solution:
We know that,
Total load, P = Load on steel rod + Load on copper tube

We know that,
Change in length of steel rod = Change in length of copper tube

Lengths of the steel rod and copper tubes are equal.
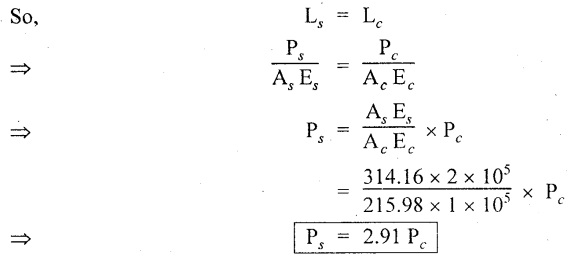
Substituting P, value in equation (A),

Result:
σc = 59.21 N/mm2; σs = 118.45 N/mm2
Example 1.27:
A steel rod of 20 mm diameter is enclosed centrally in a hollow copper tube of external diameter 30 mm and internal diameter 25 mm. The composite bar is then subjected to an axial pull of 40 kN. Find the stresses in the rod and tube. Take Es = 200 kN/mm2 and EC = 100 kN/mm2.
Given:
Steel rod diameter = 20 mm
Area of steel rod = π / 4 (20)2

Copper Tube:
External diameter, D = 30 mm
Internal diameter, d = 25 mm

Force, P = 40 kN = 40 × 103 N
Es = 200 kN/mm2
= 200 × 103 N/mm2
Ec = 100 kN/mm2
= 100 × 103 N/mm2
To find:
Stress in the rod and tube.
Solution:
We know that,
Total load, P = Load on steel rod + Load on copper tube
P = Ps + Pc
40 × 103 = Ps + Pc

We know that,
Change in length of steel rod = Change in length of copper tube

Lengths of the steel rod and copper tube are equal.
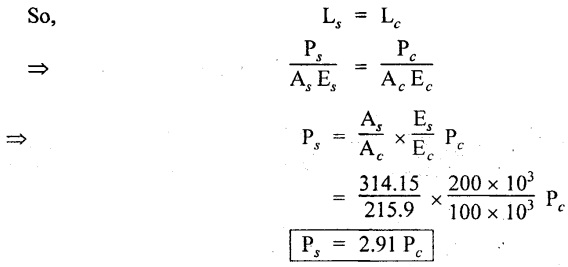
Substituting in (A),

Result:
σc = 47.38 N/mm2; σs = 94.76 N/mm2
Example 1.28:
A steel rod of 20 mm diameter is enclosed centrally in a hollow copper tube of external diameter 40 mm and internal diameter 35 mm. The composite bar is then subjected to an axial pull of 50 kN. Find the stress in the rod and tube. Take Es = 2.1 × 105 N/mm2. Ec = 1 × 105 N/mm2.
Given:
Steel rod diameter = 20 mm
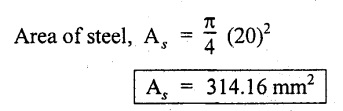
Copper tube:
External diameter, D = 40 mm
Internal diameter, d = 35 mm

Force, P = 50 kN = 50 × 103 N.
Es = 2.1 × 105 N/mm2;
Ec = 1 × 105 N/mm2
To find:
Stress in the steel rod and tube.
Solution:
We know that,
Total load, P = Load on steel rod + Load on copper

We know that,
Change in length of steel rod = Change in length of copper tube

Lengths of the steel rod and copper tube are equal.
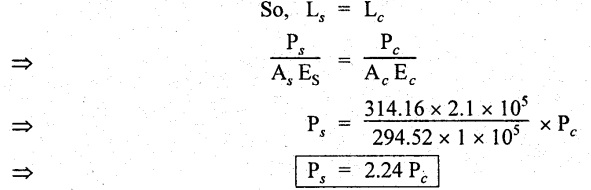
Substituting Ps value in equation (A),
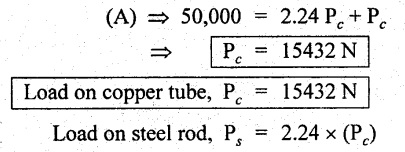
= 2.24 × (15432)

Result:
Stress in the steel rod, σs = 110 N/mm2
Stress in the copper tube, σc = 52.4 N/mm2
Example 1.29:
A reinforced concrete column 300 × 300 mm has 4 reinforcing steel bars of 25 mm diameter in each corner. Find the safe axial load on the column when the concrete is subjected to a stress of 5 N/mm2. What is the corresponding stress in steel. Take Es/Ec = 18.
Given:
Area of column = 300 × 300 = 90,000 mm2
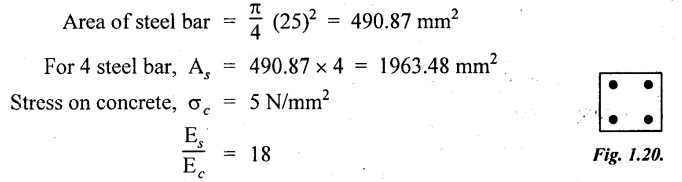
To find:
(1) Load, P, (2) Stress in the steel, σs
Solution:
Area of concrete =Area of column Area of steel
= 90,000 - 1963.48
We know that,
Total load, P = Load on steel bar + Load on concrete

We know that,
Change in length of steel bar = Change in length of concrete

Length of the bar and concrete rod are equal.

Substituting Pc value in Equation (B),

Substituting Pc, Ps values in Equation (A),

Result:
Total load, P = 616255.6 N
Stress in steel, σs = 89.67 N/mm2
Example 1.30:
A reinforced concrete column 300 × 300 mm is reinforced with 8 steel rods with a total area of 1820 mm2. The column carries an axial load of 400 kN. If the modulus of elasticity of steel is 18 times that of concrete, find the stresses in concrete and in steel.
Given:
Area of column = 300 × 300
= 90,000mm2
Area of column = 90,000 mm2
Total area of steel rod, As = 1820 mm2
Axial load, P = 400 kN = 4,00,000 N

To find:
Stresses in concrete and steel.
Solution:
Area of concrete = Area of column - Area of steel
= 90,000 - 1820
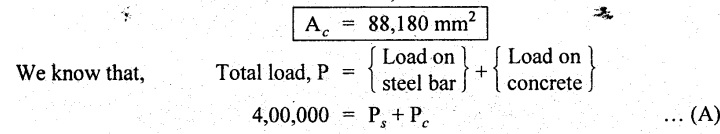
We know that,
Change in length of steel bar = Change in length of concrete

Length of steel bar and concrete bar are equal.
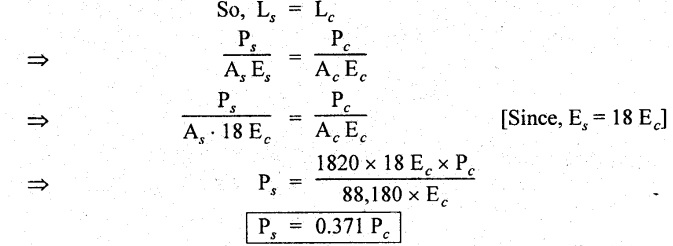
Substituting in equation (A),

Result:
Stress in concrete, σc = 3.3 N/mm2
Stress in steel, σc = 59.47 N/mm2
27. TEMPERATURE STRESS AND STRAIN
When a material is free to expand or contract due to change in temperature, no stress and strain will be developed in the material. But when the material is rigidly fixed at both the ends, the change in length is prevented. Due to change in temperature, stress will be developed in the material. Such stress is known as temperature or thermal stress and the corresponding strain is known as thermal strain. In other words, thermal stress is the stress developed in material due to change in temperature.
28. DETERMINATION OF THERMAL STRESS AND STRAIN
Consider a rod AB of length L, fixed at both ends A and B as shown in Fig.1.22. When the temperature of the rod is raised, it tends to expand by αTL. Where α is the coefficient of linear expansion.
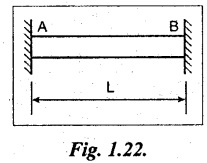
When the fixture at the end B is removed, the rod is freely expanded by αTL. From that we came to know BB' = αTL.
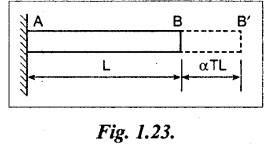
Compressive load P is applied at B', the rod is decreased in its length from L + αTL to L as shown in Fig.1.24 and 1.25.

We know that,

We know that,

Suppose a rod of length L, when subjected to a rise of temperature is permitted to expand only by δ, then
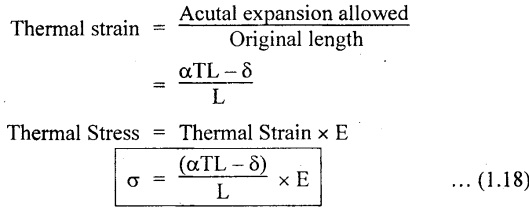
29. SOLVED PROBLEMS
Example 1.31:
A rod of 3 m long is initially at a temperature of 15 °C and it is raised to 90°C. Find the expansion of the rod and if the expansion is prevented, |find the stress in the material.
Take E = 2 × 105 N/mm2: α = 12 × 10-6/°C
Given:
Length, L = 3 m = 3000 mm
Increase in temperature, T = 90°C - 15°C = 75 °C
Young's modulus, E = 2 × 105 N/mm2
Coefficient of linear expansion, α = 12 × 10-6/°C
To find:
1. Expansion of the rod.
2. Stress in the material.
Solution:
We know that,

When expansion is prevented,

Result:
1. Expansion of the rod = 2.7 mm
2. Thermal Stress = 180 N/mm2
Example 1.32:
A rod of 1.5 m long, 10 mm diameter is fixed at the ends and subjected to axial pull of 8 kN. Find the residual stress due to increase in temperature of 25 °C.
Take E = 2.1× 105 N/mm2; α = 15 × 10-6/°C.
Given:
Length of the rod, L = 1.5 m = 1500 mm
Diameter of the rod, D =10 mm
Axial pull, P = 8 KN = 8000 N
Increase in temperature, T = 25°C
Young's modulus, E = 2.1 × 105 N/mm2
Coefficient of linear expansion, α = 15 × 10-6/°C
To find:
Residual Stress.
Solution:
We know that,

There will be increase in length of the rod due to increase in temperature. This increased length is prevented due to fixed ends and the compressive stress is induced in that rod.

Result:
Residual Stress = 23.1 N/mm2
Example 1.33:
A steel rod of 4 m long and 30 mm diameter is connected to two grips and the rod is maintained at a temperature of 70°C. Find out the force exerted by the rod after it has been cooled to 25 °C, if (a) the ends do not yield, and (b) the ends yield by 1.5 mm.
Take E = 2.1 × 105 N/mm2; α = 12 × 10-6 / °C
Given:
Length of the steel rod, L = 4 m = 4000 mm
Diameter, D = 30 mm
Decrease in temperature, T = 70°C -25°C
T = 45°C
Coefficient of linear expansion, α = 12 × 10-6/°C
Young's Modulus, E = 2.1 × 105 N/mm2
To find:
Force exerted by the rod,
(a) When the ends do not yield
(b) When the ends yield by 1.5 mm
Solution:
(a) When the ends do not yield:
Thermal stress, σ = αTE
= 12 × 10-6 × 45 × 2.1 × 105
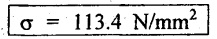
Force exerted by the rod or pull

(b) When the ends yield by 1.5 mm
δ = 1.5 mm
The thermal stress when the ends yield is given by

Force exerted by the rod or pull

Result:
Force exerted by the rod
(a) P = 80,157.7 N, when the ends do not yield.
(b) P = 24,492.6 N, when the ends yield by 1.5 mm.
30. TEMPERATURE STRESSES IN BARS OF VARYING CROSS SECTION
Consider a bar of varying cross section as shown in Fig.1.26. This bar is fixed at A and C and subjected to temperature variation. When the temperature varies, the bar will tend to expand or contract. But the same is prevented as it is fixed at both ends, so that, the temperature stress will be produced in that bar.
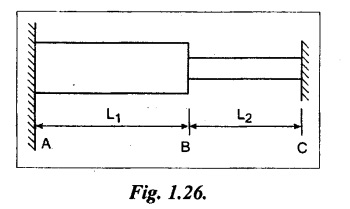
Let
L1 - Length of portion AB
σ1 - Stress induced in portion AB
A1 - Cross sectional area of portion AB.
L2 - Length of portion BC.
σ2 - Stress induced in portion BC.
A2 - Cross sectional area of portion BC.
E - Young's Modulus of the material
α - Co efficient of linear expansion
T - Temperature variation.
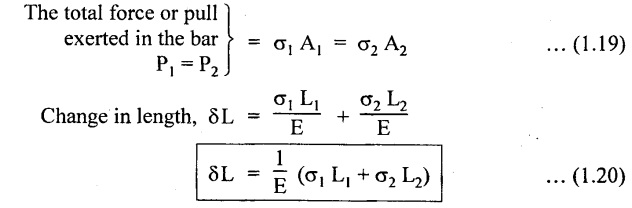
When the materials having different modulus of elasticity,

31. SOLVED PROBLEMS
Example 1.34:
A rod made of brass and steel is held between two rigid supports C and E as shown in Fig. 1.27. Find the stresses in each material if the temperature rises by 50°C.
Take
Eb = 1.1 × 105 N/mm2;
Es = 2.1 × 105 N/mm2;
αb = 18 × 10-6 /°C;
αs = 12 × 10-6/°C
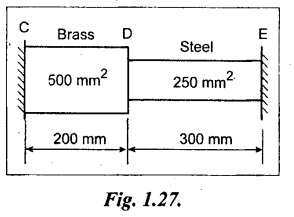
Given:
Area of brass rod, Ab = 500 mm2
Length of brass rod, Lb = 200 mm
Area of steel rod, As = 250 mm2
Length of steel rod, Ls = 300 mm
Rise in temperature for both brass and steel portion T = 50°C
Young's modulus of brass, Eb = 1.1 × 105 N/mm2
Young's modulus of steel, Es = 2.1 × 105 N/mm2
Coefficient of linear expansion of brass, αb = 18 × 10-6 / °C
Coefficient of linear expansion of steel, αs = 12 × 10-6/°C
To find:
1. Stress in brass, σb
2. Stress in steel, σs.
Solution:
We know that,

From equation (1.21), we know that,
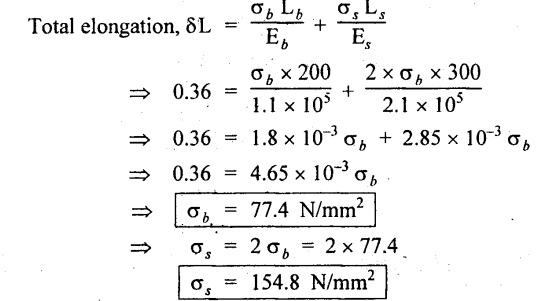
Result:
Stress in brass, σb = 77.4 N/mm2
Stress in steel, σs = 154.8 N/mm2
Example 1.35:
A rod is made of brass, copper and aluminium, as shown in Fig.1.28 is held between two rigid supports at A and D. Calculate the stresses developed in each material when the temperature of the system is raised by 40°C. Take Es = 2.1 × 105 N/mm2.

Given:
Area of the steel, As = 100 mm2
Length of the steel, Ls = 75 mm
Area of the copper, Ac = 200 mm2
Length of the copper, Lс = 150 mm
Area of the aluminium, Aa = 400 mm2
Length of the aluminium, La = 200 mm
Rise in temperature, T = 40°C
Young's modulus of steel, Es = 2.1 × 105 N/mm2
Young's modulus of copper, Ec = 1.1 × 105 N/mm2
Young's modulus of aluminium, Ea = 0.7 × 105 N/mm2
Coefficient of linear expansion of steel, αs = 12 × 10-6/ °C
Coefficient of linear expansion of copper, αs = 17 × 10-6/ °C
Coefficient of linear expansion of aluminium, αa = 21 × 10-6/ °C
To find:
1. Stress in steel, σs.
2. Stress in copper, σc.
3. Stress in aluminium, σa.
Solution:
We know that,

We know that,

From equation (1.21), we know that

Result:
1. Stress in steel, σs = 174.55 N/mm2
2. Stress in copper, σc = 87.27 N/mm2
3. Stress in aluminium, σa = 43.63 N/mm2
Example 1.36:
Calculate the values of the stress and strain in portions AC and CB of the steel bar shown in Fig.1.29. A close fit exists at both of the rigid supports at room temperature and the temperature is raised by 75 °C. Take E = 200 GPa and α = 12 × 10-6/°C for steel. Area of cross section of AC is 400 mm2 and of BC is 800 mm2. 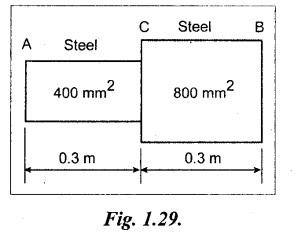
Given:
Length of steel bar at portion, AC = 0.3 m
= 300 mm
Length at portion, CB = 0.3 m
= 300 mm
Area of portion, AC = 400 mm2
Area of portion, CB = 800 mm2
Temperature rise, T = 75°C
Young's modulus of steel, E = 200 GPa
= 200 × 109 Pa
= 200 × 109 N/m2
= 200 × 103 N/mm2
E = 2 × 105 N/mm2
Coefficient of linear expansion, α = 12 × 10-6/°C
To find:
1. Stress and strain in portion, AC.
2. Stress and strain in portion, CB.
Solution:
We know that,
Elongation of steel in part AC,

We know that,

⇒ σAC = E × eAC
= 2 × 105 × 900 × 10-6

Elongation of steel in part CB

Result:
1. Strain in portion AC = 900 × 10-6
Stress in portion AC = 180 N/mm2
2. Strain portion CB = 900 × 10-6
Stress in portion CB = 180 N/mm2
32. TEMPERATURE STRESSES IN COMPOSITE BARS
A composite member is composed of two or more different materials which are joined together. Fig.1.30 Shows the composite bars consisting of brass and steel which are subjected to temperature variation. Due to different coefficient of linear expansion, the two materials (brass and steel) expand or contract by different amount
When the ends of bars are rigidly fixed, then the composite section as a whole will expand or contract. Since the linear expansion of brass is more than that of steel, the brass will expand more than steel. So, the actual expansion of the composite bars will be less than that of brass. Therefore, brass will be subjected to compressive stress, whereas steel will be subjected to tensile stress.

Let Ab = Area of cross section of brass bar.
σb = Stress in brass bar.
eb = Strain in brass bar.
αb = Coefficient of linear expansion for brass bar.
Eb = Young's modulus for brass bar.
As, σs, es, αs and Es - corresponding values of area, stress, strain, coefficient of linear expansion and Young's modulus for steel bar.
δ = Actual expansion of the composite bar.
We know that,

Similarly,
Load on the steel, Ps = σs × As
Under equilibrium condition, compression in the brass bar is equal to tension in the steel bar.
i.e., Load on the brass = Load on the steel

We know that,

Substituting equation (1.24) and (1.25) in equation (1.23),
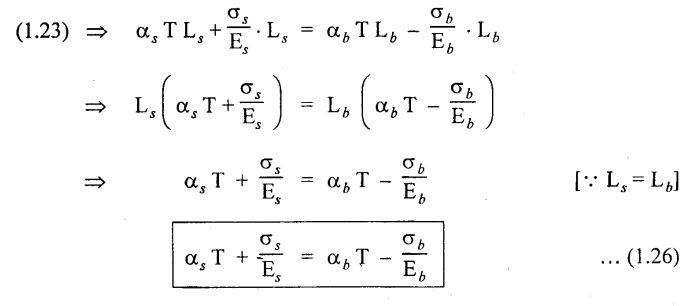
33. SOLVED PROBLEMS
Example 1.37:
A steel rod of 30 mm diameter passes centrally through a copper tube of 60 mm external diameter and 50 mm internal diameter. The tube is closed at each end by rigid plates of negligible thickness. Calculate the stress developed in copper and steel when the temperature of the assembly is raised by 60°C.
Take E for steel = 2 × 105 N/mm2
E for copper = 1 × 105 N/mm2
α for steel = 12 × 10-6/°C
α for copper = 18 × 10-6/°C
Given:
Diameter of steel, Ds = 30 mm
External diameter of copper, Dc = 60 mm
Internal diameter of copper, dc = 50 mm
Rise in temperature, T = 60°C
Young's modulus for steel, Es = 2 × 105 N/mm2
Young's modulus for copper, Ec = 1 × 105 N/mm2
Coefficient of linear expansion for steel, αs = 12 × 10-6 /°C
Coefficient of linear expansion for copper, αc = 18 × 10-6/°C
To find:
1. Stress developed in steel, σs.
2. Stress developed in copper, αc.
Solution:

Since the ends of the bars are rigidly fixed, the composite section as a whole. will expand or contract. In this problem, the coefficient of linear expansion of the copper is more than that of steel. So, the copper will expand more than steel. But the actual expansion of the composite bars will be less than that of copper. Therefore, copper will be subjected to compressive stress, where as steel will be subjected to tensile stress.
We know that,

Under equilibrium condition,
Compression in the copper bar is equal to tension in the steel bar.
i.e., Load on the copper = Load on the steel

We know that,
Actual expansion of steel = Actual expansion of copper
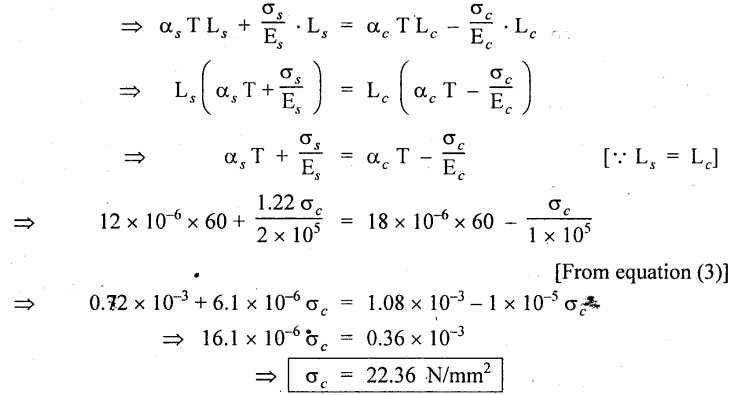
From equation (3), we know that,
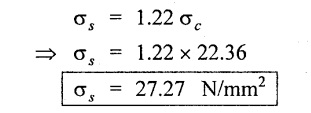
Result:
1. Stress developed in steel, σs = 27.27 N/mm2
2. Stress developed in copper, σc = 22.36 N/mm2
Example 1.38:
A gun metal rod 25 mm diameter screwed at the end passes through a steel tube 30 mm and 35 mm internal and external diameters. The temperature of the whole assembly is raised to 125°C and the nuts on the rod are then screwed lightly home on the ends of the tube. Calculate the stresses developed in gun metal and steel tube when the temperature of the assembly has fallen to 20°C.
Take
Eg = 1 × 105 N/mm2; Es = 2.1 × 105 N/mm2
αg = 20 × 10-6/°C; αs = 12 × 10-6/°C
Given:
Diameter of gun metal rod, Dg = 25 mm
External diameter of steel tube, Ds = 35 mm
Internal diameter of steel tube, ds = 30 mm
Fall in temperature, T = 125 – 20°C = 105°C
Young's modulus for steel, Eg = 1 × 105 N/mm2
Young's modulus for gun metal, Es = 2.1 × 105 N/mm2
Coefficient of linear expansion for gun metal, αg = 20 × 10-60 /°C
Coefficient of linear expansion for steel, αs = 12 × 10-6 /°C
To find:
1. Stress developed in gun metal, σg.
2. Stress developed in steel, σs.
Solution:
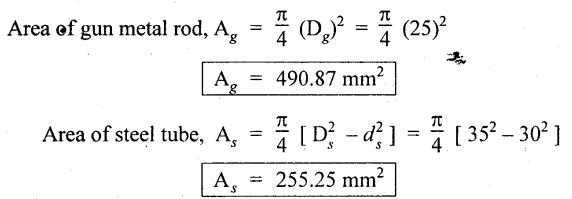
Coefficient of linear expansion of gun metal is more than that of steel. So, gun metal will be subjected to compressive stress whereas steel will be subjected to tensile stress.
We know that,

Similarly,
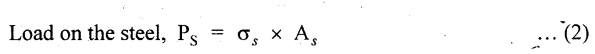
Under equilibrium condition,
Compression in the gun metal is equal to tension in the steel tube.
i.e., Load on the gun metal = Load on the steel tube

We know that,
Actual expansion steel = Actual expansion of gun metal

We know that,

Result:
1. Stress developed in gun metal, σg = 43.97 N/mm2
2. Stress developed in steel tube, σs = 84.42 N/mm2
Example 1.39:
A steel tube of 50 mm external diameter and 30 mm internal diameter encloses a copper rod of 25 mm diameter. The tube is closed at each end by rigid plates of negligible thickness. If, at a temperature of 20°C there is no longitudinal stress, calculate the stresses in the rod and tube when the temperature is raised to 220°C.
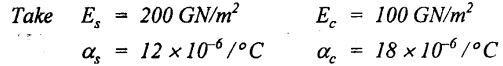
Given:
External diameter of steel tube, Ds = 50 mm
Internal diameter of steel tube, ds = 30 mm
Diameter of copper rod, Dc = 25 mm
Rise in temperature, T = 220°C – 20°C = 200°C
Young's modulus of steel, Es = 200 GN/m2
= 200 × 109 N/m2 = 200 × 103 N/mm2
= 2 × 105 N/mm2
Young's modulus of copper, Ec = = 100 GN/m2
= 100 × 109 N/m2
= 100 × 103 N/mm2
= 1 × 105 N/mm2
Coefficient of linear expansion of steel, αs = 12 × 10-6 /°C
Coefficient of linear expansion of copper, αc = 18 × 10-6 /°C
To find:
1. Stress developed in steel tube, σs.
2. Stress developed in copper, σc.
Solution:

Coefficient of linear expansion of copper is more than that of steel. So, copper will be subjected to compressive stress whereas steel will be subjected to tensile stress.
We know that,
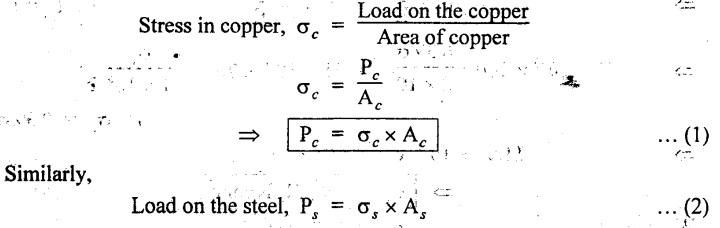
Under equilibrium condition,
Compression in the copper bar is equal to tension in the steel tube.
i.e., Load on the copper = Load on the steel

We know that,
Actual expansion of steel = Actual expansion of copper
 Result:
Result:
1. Stress developed in copper rod, σc = 100.41 N/mm2
2. Stress developed in steel tube, σs = 39.16 N/mm2
34. ELASTIC CONSTANTS
There are three types of elastic constants. They are –
1. Modulus of Elasticity or Young's Modulus (E),
2. Bulk Modulus (K) and
3. Shear Modulus or Modulus of Rigidity [G or C].
We know that the length of a bar increases by axial tension. But at the same time, there is a reduction of the lateral dimension of the bar. So when a body is loaded axially, it deforms longitudinally as well as transversely and the following strains are developed.
(i) Longitudinal strain and
(ii) Lateral strain.
35. LONGITUDINAL STRAIN
The ratio of axial deformation to the original length of the body is known as longitudinal or linear strain.

36. LATERAL STRAIN
Consider a circulår bar of length (l) and diameter (d) subjected to an axial load P as shown in Fig.1.31. The length of the bar will increase while the diameter of the bar will decrease.

where,
δL - Increase in length.
Δd - Decrease in diameter

In case of Rectangular bar,
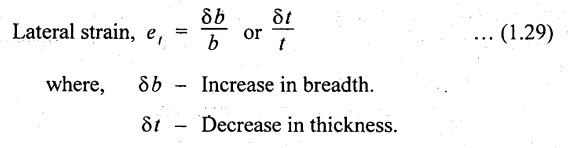
where, δb - Increase in breadth.
δt - Decrease in thickness.
37. POISSON'S RATIO
When a body is stressed, within its elastic limit, the ratio of lateral strain to the longitudinal strain is constant for a given material.

38. VOLUMETRIC STRAIN (ev)
The ratio of change in volume to the original volume is known as volumetric strain (ev).

39. VOLUMETRIC STRAIN OF A RECTANGULAR BAR SUBJECTED TO AN AXIAL FORCE (P) IS GIVEN BY

where,
δL - Change in length.
L - Original length.
1/m - Poisson's ratio.
40. VOLUMETRIC STRAIN OF A CYLINDRICAL ROD SUBJECTED TO AN AXIAL FORCE (P) IS GIVEN BY
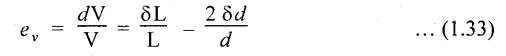
where,
δL - Change in length.
L - Original length.
δd - Change in diameter.
d - Original diameter.
41. VOLUMETRIC STRAIN OF RECTANGULAR BAR SUBJECTED TO THREE FORCES WHICH ARE MUTUALLY PERPENDICULAR IS GIVEN BY
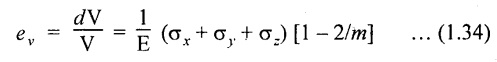
42. YOUNG'S MODULUS OR MODULUS OF ELASTICITY, E
When a body is stressed, within its elastic limit, the ratio of tensile stress to the corresponding tensile strain is constant. This ratio is known as Young's modulus.

43. BULK MODULUS, K
When a body is stressed, within its elastic limit, the ratio of direct stress to the corresponding volumetric strain is constant. This ratio is known as Bulk modulus.

where, σ - Stress.
ev = Volumetric strain.
44. MODULUS OF RIGIDITY OR SHEAR MODULUS (G)
When a body is stressed, within its elastic limit, the ratio of shearing stress to the corresponding shearing strain is constant. This ratio is known as Modulus of Rigidity and it is denoted by G or C or N.

45. RELATIONSHIP BETWEEN MODULUS OF ELASTICITY, E AND MODULUS OF RIGIDITY, G
Consider a cube of length L subjected to a shear stress of (t) shown in Fig. 1.32(a). Due to their stresses, the cube will be subjected to a deformation in such a way that the diagonal BD is elongated and the diagonal AC will be shortened. Let this shear stress (τ) cause shear strain (ϕ) as shown in Fig.1.32(b).

Substituting ϕ value in equation (1.38),

From that we know, longitudinal strain of the diagonal BD is half of the shear strain.

Substituting ϕ value in Equation (1.39),

Tensile strain on the diagonal BD is due to tensile stress and is given by Young's modulus,

Tensile strain on the diagonal BD is due to compressive stress on the diagonal AC which is given by Poisson's ratio,

Equating (1.40) and (1.43),

46. RELATION BETWEEN BULK MODULUS (K) AND YOUNG'S MODULUS (E)
Consider a cube A B C D E F G H subjected to three mutually perpendicular tensile stresses of equal intensity as shown in Fig. 1.33.

Now consider the deformation of one side (AB) of cube under the action of three mutually perpendicular stresses. This side will suffer the following three strains.
1. Tensile strain of AB is equal to σ/E due to stresses on the faces AEHD and BFGC.

2. Compressive lateral strain of AB is equal to 1/m × σ/E due to stresses on the faces AEFB and DHGC.
Poisson's ratio (1/m)
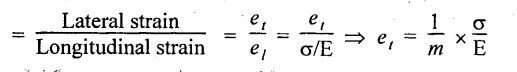
3. Compressive lateral strain of AB is equal to 1/m x σ/E due to stresses on the faces ABCD and EFGH.
Total strain of AB is given by,
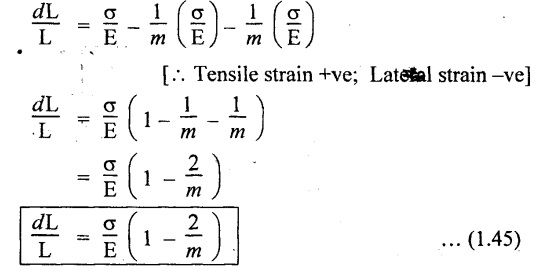
We know that, original volume of cube V = L3
Differentiating with respect to L,
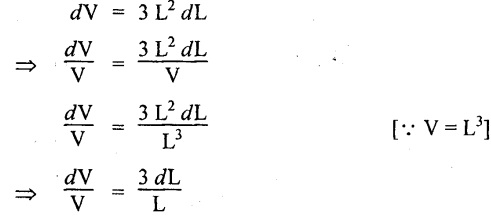
Substituting dL/L value,
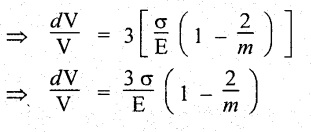
We know that,

47. FORMULAE USED

9. Volumetric strain of a rectangular bar subjected to an axial force (P) is given by,

10. Volumetric strain of a cylindrical rod subjected to an axial force (P) is given by,
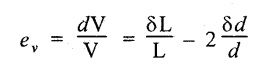
48. SOLVED PROBLEMS
Example 1.40:
Determine the change in length, breadth and thickness of a steel bar which is 5 m long, 20 mm wide and 15 mm thick subjected to an axial pull of 100 kN in the direction of its length. Take E = 200 GPa and Poisson's ratio 0.3.
Given:
Length, L = 5 m = 5000 mm
Breadth, b = 20 mm
Thickness, t = 15 mm
Axial pull, P = 100 kN = 100 × 103 N
Young's modulus, E = 200 GPa = 200 × 109 Pa
= 200 × 109 N/m2 = 200 × 103 N/mm2
Poisson's ratio, 1/m = 0.3
To find:
1. Change in length, δL,
2. Change in Breadth, δb,
3. Change in thickness, δt.
Solution:
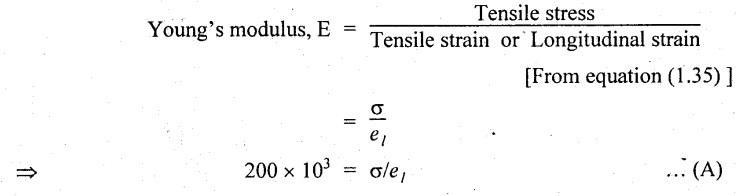

We know that,

We know that,

Result:
Change in length, δL = 8.35 mm
Change in breadth, δb = 10.02 × 10-3 mm
Change in thickness, δt = 7.51 × 10-3 mm
Example 1.41:
A bar of 20 mm diameter is tested in tension. It is observed that when a load of 40 kN is applied, the extension measured over a gauge length of 200 mm is 0.12 mm and contraction in diameter is 0.0036 mm. Find Poisson's ratio and Elastic constants E, G and K.
Given:
Diameter, d = 20 mm;
Load, P = 40 kN = 40 × 103 N;
Length, L = 200 mm;
Change in length, δL = 0.12 mm;
Change in diameter, δd = 0.0036 mm.
To find:
1. Poisson's ratio, 1/m,
2. Young's Modulus, E,
3. Modulus of Rigidity, G,
4. Bulk Modulus, K.
Solution:
We know that,

Substituting et, el values in equation (A),

We know that,

We know that,

Result:
1. Poisson's ratio, 1/m = 0.3.
2. Young's Modulus, E = 2.1 × 105 N/mm2
3. Modulus of Rigidity, G = 8.0 × 104 N/mm2
4. Bulk Modulus, K = 1.75 × 105 N/mm2
Example 1.42:
A steel bar 300 mm long, 40 mm wide and 25 mm thick is subjected to a pull of 180 kN. Determine the change in volume of the bar. Take E = 2 × 105 N/mm2 and 1/m = 0.3.
Given:
Length, L = 300 mm; Width, b = 40 mm
Thickness, t = 25 mm;
Pull, P = 180 kN = 180 × 103 N
Young's modulus, E = 2 × 105 N/mm2
Poisson's ratio, 1/m = 0.3
To find:
Change in volume.
Solution:
Volumetric strain of a rectangular bar subjected to an axial force is given by,

Substituting δL, L, 1/m values in equation (A),
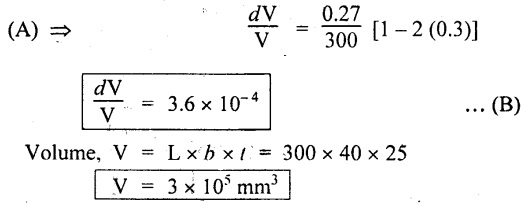
Substituting V value in equation (B),.
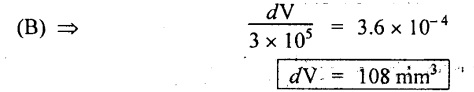
Result:
Change in volume, dV = 108 mm3
Example 1.43:
A steel rod of 20 mm diameter, 4 m long carries a tensile load of 50 kN. Calculate the change in length, diameter and volume of the rod. Take E = 2 × 105 N/mm2 and Poisson's ratio = 0.3.
Given:
Diameter, d = 20 mm;
Length, L = 4 m = 4000 mm; {
Load, P = 50 kN = 50,000 N;
Young's Modulus, E = 2 × 105 N/mm2;
Poisson's ratio, 1/m = 0.3.
To find:
1. Change in length, δL,
2. Change in diameter, δd,
3. Change in volume, δV.
Solution:
We know that,

We know that,
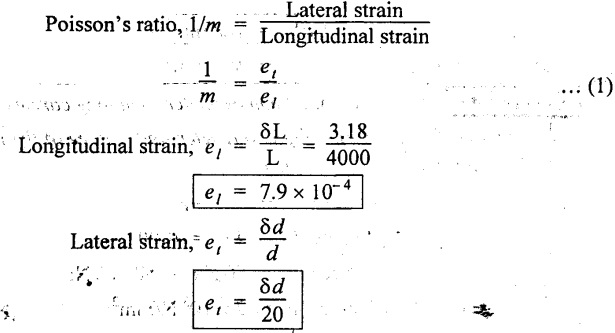
Substituting el, et, values in equation (1),
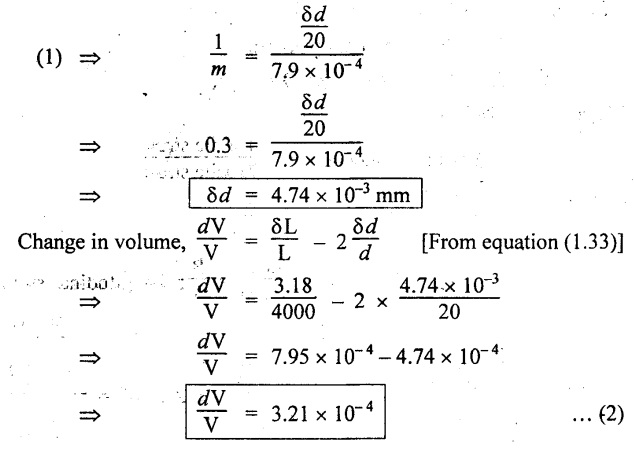
We know that,
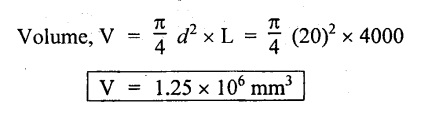
Substituting V value in equation (2),
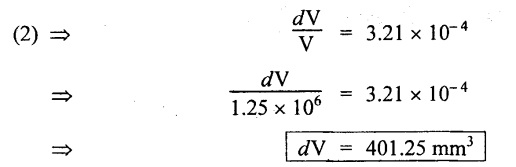
Result:
1. Change in length, δL = 3.18 mm
2. Change in diameter, δd = 4.74 × 10-3 mm
3. Change in volume, dV = 401.25 mm3
No comments:
Post a Comment