Principle of super position

 Sometimes, a body is subjected to external axial forces not only at its ends, but also at some of its interior cross sections along the length of the body.

PRINCIPLE OF SUPER POSITION

Sometimes, a body is subjected to external axial forces not only at its ends, but also at some of its interior cross sections along the length of the body. In such case, the forces are split up, and their effects are considered on individual sections. The total deformation is equal to the algebraic sum of the deformation of the individual sections. This principle of finding out the resultant deformation is known as principle of superposition.

The change in length of such member is given by,

SOLVED PROBLEMS

Example 1.13:

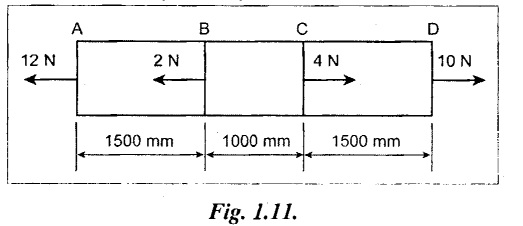
A steel rod of 50 mm diameter is subjected to a force as shown in Fig.1.11. Find the elongation of the rod. Take E = 2 × 105 N/mm2.

Given: 

Diameter of the rod, D = 50 mm

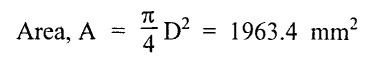
L1 = 1500 mm; L2 = 1000 mm; L3 = 1500 mm

E = 2 × 105 N/mm2

To find: 

Elongation of the rod, δL.

Solution:

Take, Tensile force is +ve [increasing length].

Compressive force is -ve [decreasing length].

Consider part AB:

Left hand side force = 12 N (Tensile)

Right hand side force = -2N (Compressive) + 4N (Tensile) + 10 (Tensile)

= 12 N (Tensile)

So, at part AB, Load is 12 N.

P1 = 12 N (Tensile)

Consider part BC:

Left hand side force = 12 N (T) + 2 N (T) = 14 N (T)

Right hand side force = 4 N (T) + 10 N (T) = 14 N (T)

So, at part BC, Load is 14 kN.

P2 = 14 N (Tensile)

Consider part CD:

Left hand side force = 12 N (T) + 2 N (T) – 4 N (C)

= 10 N (Tensile)

Right hand side force = 10 N (Tensile)

So, at part CD Load is 10 N.

P3 = 10 N (Tensile)

We know that,

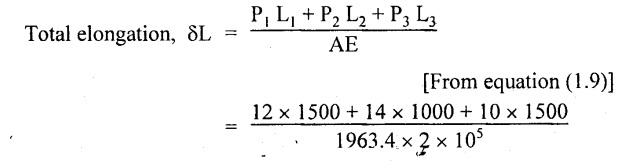
= 1.196 × 10-4 mm

Result:

Change in length, δL = 1.196 × 10-4 mm

Example 1.14: 

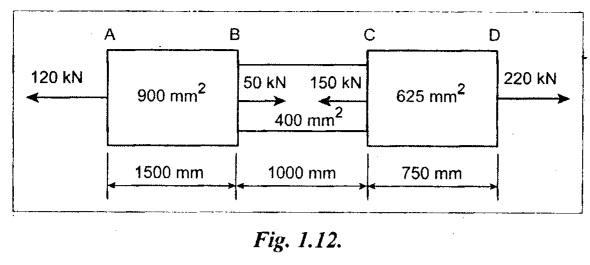
A member ABCD is subjected to loading as shown in Fig. 1.12. Determine the total elongation. Take E = 2 × 105 N/mm2.

Given:

E = 2 × 105 N/mm2

A1 = 900 mm2; A2 = 400 mm2; A3 = 625 mm2

L1 = 1500 mm; L2 = 1000 mm; L3 = 750 mm

To find: 

Total Elongation

Solution:

Take,

Tensile force is + ve [increasing length]

Compressive force is -ve [decreasing length]

Consider part AB:

Left hand side force = 120 kN (T)

Right hand side force = = 50 kN (T) – 150 kN (C) + 220 kN (T)

= 120 kN (T)

So, at part AB, Load is 120 kN.

P1 = 120 kN (T) (Tensile)

Consider part BC:

Left hand side force = 120 kN (T) – 50 kN (C)

= 70 kN (T)

Right hand side force = - 150 kN (C) + 220 kN (T)

= 70 kN (T)

So, at part BC, load is 70 kN.

P2 = 70 KN (Tensile)

Consider part CD:

Left hand side force = 120 kN (T) - 50 kN (C) + 150 kN (T)

= 220 kN (T)

Right hand side force = 220 kN (T)

So, at part CD, Load is 220 kN.

P3 = 220 kN (Tensile)

We know that,

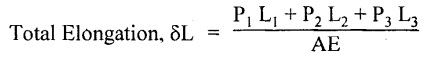
Area is not constant.

Result: 

Change in length, δL = 3.195 mm

Example 1.15: 

A bar is subjected to a point load as shown in Fig. 1.13. Calculate the force P2 and also find the total elongation of the bar. Take P1 = 60 kN and P3 = 500 kN, P4 = 150 kN and modulus of elasticity E = 2.1 × 105 N/mm2.

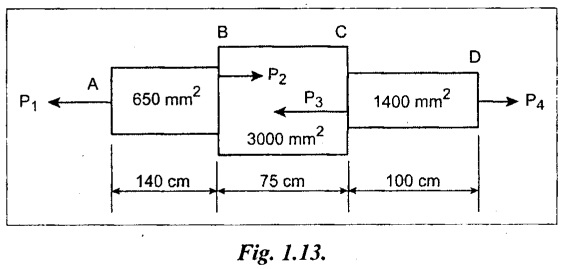
Given: 

A1 = 650 mm2; A2 = 3000 mm2; A3 = 1400 mm2

L1 = 140 cm = 1400 mm; L2 = 75 cm = 750 mm 

L3 = 100 cm = 1000 mm

P1 = = 60 kN = 60,000 N;

P3 = 500 kN = 5,00,000 N

P4 = 150 kN = 1,50,000 N; E = 2.1 × 105 N/mm2.

To find:

1. Force, P2

2. Total Elongation, δL

Solution: 

We know that,

Force acting towards right = Forces acting towards left 

Take, Tensile force is positive.

Compressive force is negative.

Consider part AB:

Left hand side force, P1 = 60 kN (T)

Right hand side force = P2 (T) - P3 (C) + P4 (T)

= 410 – 500 + 150

= 60 kN (T)

So, Load on part AB is 60 kN (T) = 60 × 103 N (T)

Consider part BC:

Left hand side force = P1 (T) - P2 (C)

= 60 kN - 410 kN

= -350 kN (C)

Right hand side force = -P3 (C) + P4 (T)

= - 500 + 150

= - 350 kN (C)

So, Load on part BC = - 350 kN (C)

= -350 × 103 N (C)

Consider part CD:

Left hand side force = P1 (T) - P2 (C) + P3 (T)

= 60 - 410 + 500

= 150 kN (T)

Right hand side force = P4 (T) = 150 kN (T)

So, at part CD load is

150 kN (T) =  150 × 103 N (T)

We know that,

Result:

1. Force, P2 = 410 kN

2. Total Elongation, δL = 0.708 mm

Example 1.16:

Calculate the force P, and change in length for the following Fig. 1.14. Take E = 200 GN/m2; P1 = 120 kN; P2 = 220 kN; and P4 = 160 kN. 

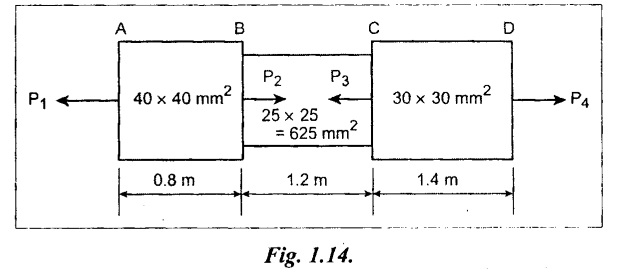
Given:

E = 200 GN/m2 = 200 × 109 N/m2

= 200 × 103 N/mm2

P1 = 120 kN = 120 × 103 N;

P2 = 220 kN = 220 × 103 N;

P4 = 160 kN = 160 × 103 N;

A1 = 40 × 40 = 1600 mm2;

A2 = 25 × 25 = 625 mm2

A3 = 30 × 30 = 900 mm2

L1 = 0.8 m = 800 mm;

L2 = 1.2 m = 1200 mm;

L3 = 1.4 m = 1400 mm.

To find: 

1. Force, P3, 

2. Change in length, SL.

Solution: 

We know that,

Forces acting towards right = Forces acting towards left 

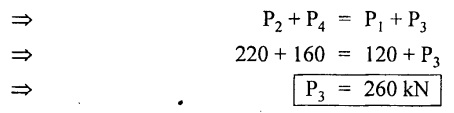
Take, Tensile force is positive.

Compressive force is negative.

Consider part AB:

Left hand side force = P1 = 120 kN (T)

Right hand side force = P2 (T) - P3 (C) + P4 (T)

= 220 - 260 + 160

= 120 N (T)

So, load on part AB is 120 × 103 N (T).

Consider part BC:

Left hand side force = P1 (T) - P2 (C)

= 120 - 220 = - 100 kN (C)

Right hand side force = - P3 (C) + P4 (T)

= -260 + 160

= -100 kN (C)

So, Load on part BC is 100 × 103 N (C)

Consider part CD:

Left hand side force = P1 (T) - P2 (C) + P3 (T)

= 120 - 220 + 260

= 160 kN (Tensile)

Right hand side force = P4 (T)

= 160 kN (T)

So, load on part CD = 160 × 103 N (T)

We know that,

Result:

1. Force, P3 = 260 kN

2. Change in length, δL = 0.58 mm

Example 1.17: 

A member ABCD is subjected to part loads as shown in Fig. 1.15. Calculate the force P necessary for equilibrium and total change in length of the bar. Take E = 210 kN/mm2. 

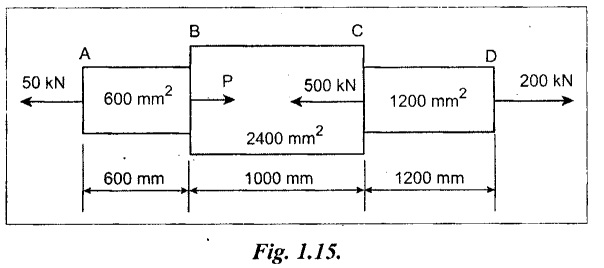
Given: 

A1 = 600 mm2; A2 = 2400 mm2; A3 = 1200 mm2

L1 = 600 mm; L2 = 1000 mm; L3 = 1200 mm

E = 210 kN/mm2 = 210 × 103 N/mm2

To find: 

(1) Force, P, (2) Total Elongation.

Solution: 

We know that,

Forces acting towards right = Forces acting towards left

P + 200 = 50 + 500

⇒ P = 350 kN

Take, Tensile force is positive.

Compressive force is negative.

Consider part AB:

Left hand side force = 50 kN (T)

Right hand side force = P (T) – 500 kN (C) + 200 kN (T)

= 350 kN (T) – 500 kN (C) + 200 kN (T)

= 50 kN (T)

So, Load on part AB = 50 × 103 N (T)

Consider part BC:

Left hand side force = 50 kN (T) - P kN (C)

= 50 kN (T) – 350 kN (C)

= 300 kN (C)

Right hand side force = - 500 kN (C) + 200 kN (T) 

= -300 kN (C)

So, Load on part BC is - 300 × 103 N (C)

Consider part CD:

Left hand side force = 50 KN(T) - P kN (C) + 500 kN (T)

= 50 kN - 350 kN + 500 KN

= 200 kN (T)

Right hand side force = 200 kN (T)

So, Load on part CD is 200 × 103 N (T)

We know that,

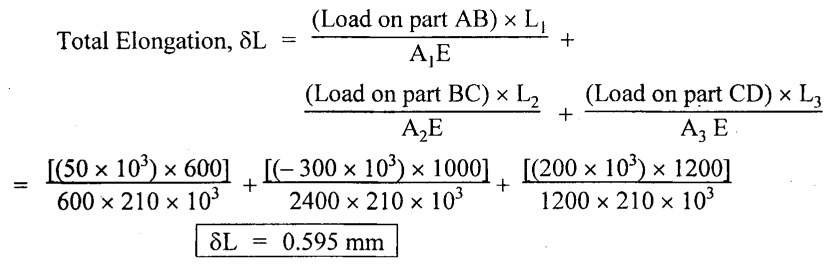
Result: 

1. Force, P = 350 kN

2. Change in length, δL = 0.595 mm