Specific Speed of Turbine

 It is defined as the speed of a turbine which is identical in shape, geometrical dimensional, blade angle, gate opening etc., with the actual turbine but of such a size that it will develop unit power when working under unit head.

SPECIFIC SPEED

It is defined as the speed of a turbine which is identical in shape, geometrical dimensional, blade angle, gate opening etc., with the actual turbine but of such a size that it will develop unit power when working under unit head. It is denoted by the symbol Ns. The specific speed is used in comparing the different type of turbines as every type of turbine has different specific speed.

In M.K.S units, power is taken as one horse power and unit head as one metre. But in S.I units, unit power is taken as one kilowatt and unit head as one metre.

1. Derivation of the specific speed

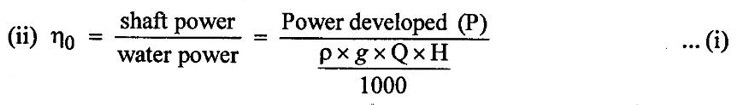
Where

H = Head under which the turbine is working in m.

Q = Discharge through turbine in m3/s

P = Power developed or shaft power in watts

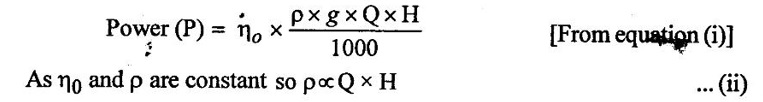
D = Diameter of actual turbine

N = Speed of actual turbine

u - Tangential velocity of the turbine

Ns = Specific speed of the turbine

V = Absolute velocity of water

The absolute velocity, tangential velocity and head on the turbine are related as,

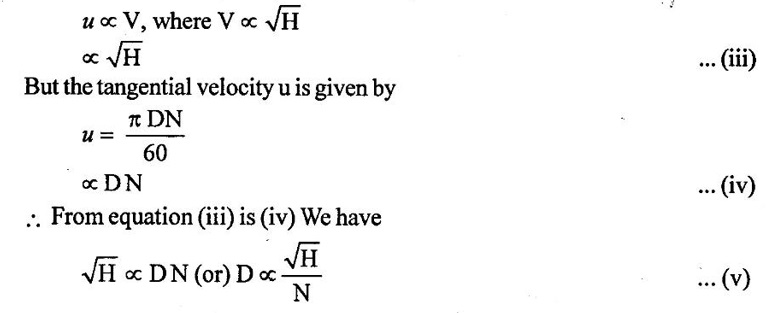
The discharge through turbine is given by

Q = Area × velocity

Substituting the value of Q in equation (ii)

Where K = constant of proportionality.

Values substituting in above equation.

Substituting the above value of K in equation (vii)

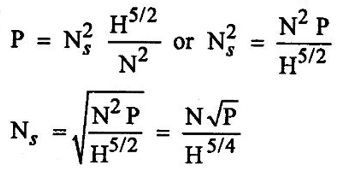
If p is taken is meteric horse power the specific speed is obtained in M.K.S units.

But if P is taken in kilowatts the specific speed obtained in SI. units.

2. Significance of specific speed

Specific speed plays an important role for selecting the type of the turbine. Also the performance of a turbine can be predicted by knowing the specific speed of the turbine. The type of turbine for different specific speed is given in table 5.5 as

3. Solved Examples based on Specific Speed

Example - 45

A turbine develops 7225 kw power under a head of 25 metres at 135 rpm. Calculate the specific speed of the turbine and state the type of the turbine. 

Given data:

Power developed P = 7225kw

Head H = 25m

Speed N = 135 rpm

To find:

Specific speed of the turbine (Ns)

Solution:

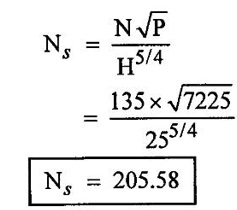
From the table 5.5 for specific speed SI between 51 and 255 the type of turbine is Francis. As the specific speed 205.28 lies in the range and hence type of turbine Francis.

Example - 46

A turbine is to operate under a head of 25m at 200 rpm. The discharge is 9 cumec. If the efficiency is 90% determine.

(i) Specific speed of the machine

(ii) Power generated and

(iii) Type of turbine

Given data:

Head H = 25m

Speed N = 200 rpm

Discharge Q = 9 cumec = 9 cumec = 9 m3/s

Efficiency η0 = 90% = 0.90

To find:

(i) Secific speed of the machine (Ns) 

(ii) Power generated 

(iii) Type of turbine 

Solution:

(iii) The specific speed lies between 51 to 255. so the turbine is a Francis turbine.

Result:

(i) S.P. speed of machine Ns = 159.46 rpm

(ii) Power generated P = 1986.5 kw

(iii) Types of turbine is Francis turbine.

Example - 47

A turbine develops 9000 kw when running at a speed of 140 rpm and under a head of 30m. Determine the specific speed of the turbine.

Given data:

Power developed P = 9000 kw

Head H = 30m

Speed N = 140 rpm

To find:

The specific speed of turbine

Solution:

Result:

The specific speed of turbine Ns = 189.167

Example - 48

A pelton turbine develops 3000 kw under a head of 300 m the overall efficiency of the turbine is 83%. If speed ratio = 0.46, Cv 0.46, Cv = 0.98 and specific speed is 16.5, then find (i) Diameter of turbine and (ii) Diameter of jet.

Given Data:

Power P = 3000 kw

Overall efficiency η0 = 83% or 0.83

Net head H = 300 m 

Speed ratio (ku) = 0.46

Specific speed (Ns) = 16.5

Value of Cv = 0.98

To find:

(i) Diameter of the turbine (D)

(ii) Diameter of jet (d)

Solution:

(iv) Diameter of the turbine (D)

(vi) Q = Area of jet × velocity

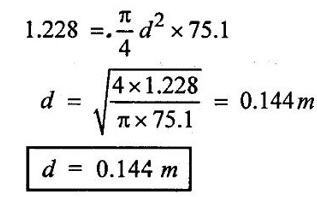
Result:

1. Diameter of the turbine D = 1.78 m

2. Diameter of the jet d = 0.144 m