Solved Problems on Buoyancy and Floatation: Fluid Properties and Flow Characteristics - Fluid Mechanics and Machinery
Solved Problems on Buoyancy and Floatation
Example - 87
A body weighs 190 N in air and 110 N what immersed in water. Find (i) Volume and (ii) Specific gravity of the body.
Give data:
Body weighs in air = 190 N
Body weighs in immersed water = 110 N

To find:
(i) Volume
(ii) Specific gravity of the body
Solution:
1) The body weighing 110 N means that the tension in the cord is 110 N of shown in figure. During equilibrium
Σρy = 0
w – T - Fb = 0
190 - 110 - Fb = 0
Fb = 80 N
2) Buoyancy force is equal to the weight of displaced water and U is volume of displaced water
Fb = U × ρ × g
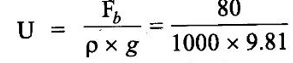
Volume (U) = 8.15 × 10-3 m3
The volume of the body = Volume of water displaced
Weight of the body
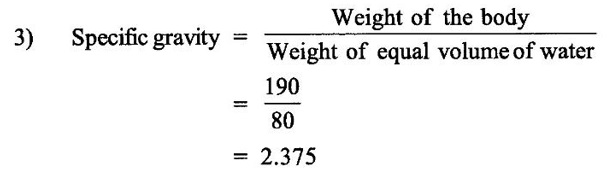
Result:
i) Volume (U) = 8.15 × 10-3 m3
ii) Specific gravity of the body = 2.375
Example - 88
A hydrometer weighs 0.04 N and it has a cylindrical stem of radius 3.0 mm. How much deeper the hydrometer will float in oil of sp. gravity 0.8 as compared to alcohol of sp. gravity 0.9?
Given data:
Hydrometer weighs = 0.04 N
Stem radius (r) = 3.0 mm
Sp. gravity of alcohol So = 0.8
Sp. gravity of alcohol Sa = 0.9

To find:
Compare the deeper of hydrometer
1) If we consider the equilibrium of hydrometer in alcohol
Weight of the hydrometer = Weight of alcohol displaced
0.04 = ρ × g × U
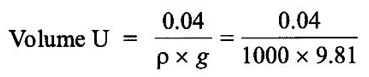
U = 4.077 × 10-6 m3
2) Now consider the equilibrium of hydrometer in oil
Volume of oil displaced = U + Ah
Weight of the hydrometer = Weight of oil displaced
= ρ × g × volume of oil displaced
= ρ × g × (U + Ah)
0.04 = 0.8 × 1000 × 9.81 (U + πr2 × h)
= 7848 (4.077 × 10−6 + π × (3 × 10−3)2 × h)
5.096 × 10-6 = 4.077 × 10−6 + 2.827 × 10−5 h
1.019 × 10-6 = 2.827 × 10-5h
h = 0.03604 m (or) 36.04 mm
Result:
h = 0.0364 m (or) 36.04 mm
Example - 89
A wooden log 4.5 m long and 10 cm square has SP gravity 0.8 what mass of lead is to be tied to one end of the log so that if floats upright with 4.2 m inside the water. Take the density of lead as 13 × 103 kg/m3.
Given data:
Wooden log length l = 4.5 m
Area A = 10 cm2 = 1 × 10-3 m2
SP. gravity of log S1 = 0.8
Density of lead p1 = 13 × 103 kg/m3

To find:
Mass of lead.
Solution:
(i) Total weight of the log and lead = weight of displaced water
Volume of log = A × l
= 1 × 10-3 × 4.5
= 4.5 × 10-3 m3
Volume of log = volume inside the water
(ii) Assume volume of lead log = weight of water displaced
4.5 × 10-2 × 0.8 × 9.81 × 1000 + U × 13 × 103 × 9.81
= (4.2 × 10-2 + U) × 1000 × 9.81
353.16 + 12730 U = 412.02 + 9810 U
127530 U - 9810 U = 412.02 + 353.16
117720 U = 58.86
U = 5 × 10-4 m3
(iii) Mass of lead = 5 × 10-4 × 13 × 103
= 6.5 kg
Result:
Mass of lead (m) = 6.5 kg
Example - 90
A metallic float is at the interface of mercury and water in such away that its 40% volume is submerged in mercury and remaining in water as shown in figure. Find the density of the float. Take density of mercury ρm = 13.6 × 103 kg/m3
Given data:
Metallic float submerged mercury=40%
Density of mercury ρm = 13.6 × 103 kg/m3

To find:
Density of the float.
Solution:
(i) Volume in mercury=0.14 U
Volume in water = U - 0.4 = 0.6 U
(ii) Weight of float = Weight of mercury displaced + weight of water displaced
U × ρƒ × g = 0.4U × ρm × g + 0.6U × ρw × g
U × g × ρƒ = U × g ((0.4 × ρm) + (0.6 × ρw))
ρƒ = 0.4 × 13.6 × 103 + 0.6 × 1000
= 5440 + 600
ρƒ = 6040 kg/m3
Result:
Density of sloat ρƒ = 6040 kg/m3.
Example – 91
If density of ice begg is 0.9 × 103 kg/m3 and that of sea water is 1.05 × 103 kg/m3, then find the percent volume of ice begg above the sea water what it floats.
Given data:
Density of ice begg = 0.9 × 103 kg/m3
Density of sea water = 1.05 × 103 kg/m3

To find:
% volume of ice begg above sea water (U1)
Solution:
(1) The weight of ice begg = weight of seawater displaced
Wice begg = U × ρicebegg × g
= (U – U1) × 1.05 × 103 × g
U × 0.9 × 103 × g = (U – U1) × 1.05 × 103 × ġ
0.9 U = 1.05 U - 1.05 U1
1.05 U1 = 1.05 U - 0.9 U
= 0.15 U
U1 / U = 0.15/1.05
= 0.1428
U1 = 0.1428 × 100
= 14.28% of total volume of the ice begg
Result:
% volume of ice begg above sea water U1 = 14.28%.
Example - 92
A submarine has volume of 1200 m3 and weight of 9 × 103 kN. Find the volume of water to be pump as ballast into submarine so that it can submerge in the water.
Given data:
Submarine volume U= 1200 m3
Submarine weight W = 9 × 103 KN

To find:
Volume of water to be pump as ballast into submarine.
Solution:
(i) Buoyancy force of submarine = Weight of water displaced.
Fb = U × ρw × g
= 1200 × 1000 × 9.81
Fb = 11.772 × 103 kN
Fb > W submarine will float.
(ii) The submarine will submerge if weight of submarine is increased to its buoyancy force (Fb). Hence if U m3 of water is to be pumped to submerge the submarine.
W + pumped water = Fb
9 × 106 + U × ρ × g = 11.772 × 106
U × 1000 × 9.81 = 11.772 × 106 - 9 × 106
= 2.772 × 106

U = 282.56 m3
Result:
Volume of water is to be pumped U = 282.56 m3.
Example - 93
A cylindrical vessel of 140 mm diameter is filled with a liquid of specific weight of 9.0 kN/m3 up to a depth of 90 mm subsequently, 110 mm diameter solid cylinder weight of 5 × 103 N and height of 92 mm and it is immersed into the liquid contained in the vessel. Determine the level at which the solid cylinder will float.
Given data:
Diameter of vessel 140 mm = 0.14 m
Liquid SP weight in vessel = 9.0 kN/m3 = 9 × 103 N/m3
Height of liquid in the vessel = 90 mm = 0.09 m
Diameter of solid cyclinder = 110 mm = 0.11 m
Weight solid cyclinder = 5 × 10-3 N
Height of solid cyclinder = 92 mm = 0.092 m
To find:
Depth of solid cyclinder submerge in the vessel.
Solution:

(3) Weight of solid cyclinder = Buoyance force
SP.weight of solid cylinder × volume of cylinder submerged
5 × 10-3 = 9 × 103 × π/4 × (0.11)2 × (h + y)
5 × 10-3 = 85.527 × (h + y)
(h + y) = 5.846 × 10−5. ... (ii)
(iv) Equation (i) apply in equation (ii)
0.015 y + y = 5.846 × 10-5
y = 5.759 × 10-5 m
h = 0.015 y
= 0.15 × 5.759 × 10-5
h = 8.639 × 10-6 m
Result:
Depth of solid cyclinder submerged (h) = 8.639 × 10-6m
Example - 94
A wooden log, 0.9 m in diameter × 5 m in length floats in floating lake water. If the log has a specific gravity 0.65, calculate the depth of immersion of wooden log.
Given data:
Diameter of wooden log, d = 0.9 m
Length of wooden log, L = 5 m
Specific gravity of log s = 0.65
To find:
Depth of immergion of wooden log.

Solution:
(1) SP. weight of log = Weight / Volume
Weight of log = SP.weight of log × volume of log
= SP. gravity of log × SP. weight of weight × volume of log
= S × Wwater × π/4 × d2 × L
= 0.65 × 9810 × π/4 × (0.9)2 × 5
Wlog = 20.282 × 103 N
(2) Weight oflog = Weight of water displaced
= ρw × g × volume of water displaced
Volume of water displaced =

Volume of woodent log and underwater = 2.067 m3
(3) Volume of wooden log under water = (From figure) area ABCD × length
Area ABCD = 2.067 / 5
Area ABCD = 0.413 m2
(4) Area ABCD = Area ABCOA + Area AOB

0.413 = 0.636 - 3.53 × 10-3θ + 0.101sin 2θ
3.53 × 10-3 θ – 0.101 sin2 θ = 0.223
θ - 28.61 sin 2 θ = 63.17
By hit and trial θ = 76.54°
(5) Depth of wooden log in water h = t + t cos θ
= 0.45 + 0.45 × cos 76.54
= 0.554 m
Result:
Depth of wooden log in water h = 0.554 m.
Example - 95
A rectangular solid body of 8 m long, 5 m wide and 2 m deep is immersed 1.5 m in sea water calculate the metacentric height, if the density of sea water is 1100 kg/m3.
Given data:
Size of rectangular body = 8 × 5 × 2
Depth of immergion = 1.5 m
Density of seawater ρsw = 1100 kg/m3
To find:
Metacentric height.
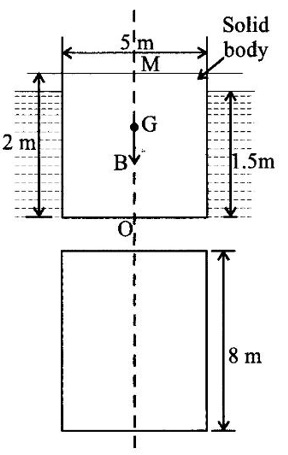
Solution:
(1) Distance of centre of buoyancy from the bottom of the block OB
= 1.5 / 2 = 0.75 m.
(2) Distance of centre of gravity from the bottom of the block OG = 2/2 = 1m
BG = OG - OB
= 1 - 0.75
= 0.25 m

(4) Volume of water displaced (V) = 8 × 5 × 1.5
= 60 m3
(5) Metacentre BM = I/U = 83.33/60 = 1.388 m
Metacentric height GM = BM - BG
= 1.388 - 0.25
GM = 1.138 m
Result:
Metacentric height GM = 1.138 m
Example - 96
A cyclindrical body of 5 m diameter and 7 m long is weighing 250 kN. Check whether the solid body is float of not.
Given data:
Diameter (d) = 5m
Length (L) = 7m
Weight (w) = 250 kN = 250 × 103 N
To find:
Solid body float of not.
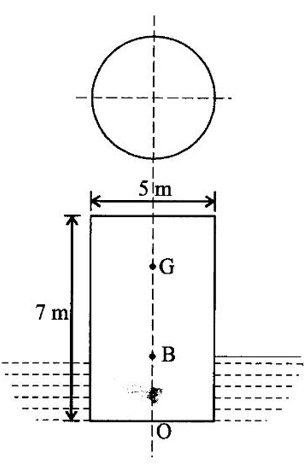
Solution:

(6) Metacentric height GM = BM – BG = 1.204 - 2.85
GM = 1.646 m
Result:
Metacentric height is negative, hence it cannot float.
Example - 97
A cyclinder made of wood is having diameter 'd' and length '2d' floating in water with the axis vertical. State whether the cyclinder is in equilibrium stable of not. Find also the metacentric height. Take the specific gravity of wood is 0.8.
Given data:
Dia of cyclinder = d
Length of cyclinder = 2d
Specific gravity of wood = 0.8
To find:
Eqilibrium stable of cyclinder
Solution:

Result:
Meta centric height GM = BM - BG
(i) GM is negative so this is unstable = 0.039 d - 0.2 d
(ii) Meta centre depth = OB – BM = 0.8 d - 0.039 d = −0.16 m
= 0.761 d
Example - 98
A cyclindrical buoy having diameter 3 m and 1.8 m high weighing 6 kN is floating in sea water with its axis vertical. Find the maximum allowable height above the top of the buoy of the centre of gravity of a 500 N load which is centrally placed at the top of the buoy. Take specific gravity of sea water as 1.04.
Given data:
Diameter D = 3 m
Height h = 1.8 m
Weight w = 6 kN = 6000 N
Buoy of ca = 500 N
SP gravity of seawater (s) = 1.04
To find:
Maximum allowable height above top of the buoy 500 N.
Solution:

(8) For stable equilibrium of the floating body
BM > BG'
6.24 > 0.830 + 0.0769 x
x = 70.35 m
Result:
The centre of gravity of load should be more than 70.35 - 6.24 = 64.11 m above the top of the buoy.
Example - 99
A hollow wooden cyclinder of specific gravity 0.8 has an outer diameter of 70 cm and an inner diameter of 35 cm. It is requited to float in oil of specific gravity 0.95. Find the maximum length of the cylinder so that it shall be stable when floating with its axis vertical and depth to which it will sink.
Given data:
Outer diameter Do = 70 cm = 0.7 m
Inner diameter D1 = 35 cm = 0.35 m
SP. gravity of wood Swood = 0.8
SP. gravity of oil soil = 0.95
To find:
(i) Maximum length of cyclinder floating in stable.
(ii) Depth of sink.
Solution:
 Result:
Result:
(i) Maximum length l = 0.757 m
(ii) Depth of immersion (h) = 0.637 m
Example - 100
A ship of weight 15 MN has horizontal cross-section of water line as shown in the figure. If it has its centre of gravity is at a depth 70 cm from the free surface, find its meta centre height for rolling (about x-x axis) for pitching (about y-y axis). The ship has centre of buoyancy at a depth of 320 cm below the free surface.
Given data:
Depth of centre of gravity = 0.7 m
Depth of centre of buoyancy = 3.2 m
Ship weight = 15 MN = 15 × 106 N
Buoyancy depth = 320 cm = 3.2 m
To find:
Meta centric height
(i) Rolling
(ii) Pitching
Solution:

Result:
(i)
For rolling Gm = 1.64 m
(ii) For pitching Gm = 71.84 m
Example - 101
A reactangular pontoon is 10 m long, 8 m wide and 4 m hight. It weihs 800 kN. It carries on its upper deck an empty boiler 4 m in diameter which weighs 400 kN. If the centre of gravity of the pontoon and boiler are at their geometric centre on the normal axis, find the stability of the pontoon.
Given data:
Pontoon size = 10 m × 8m × 4m
Weights w = 800 kN
Diameter of boiler = 4 m
Weigh of boiler = 400 kN
To find:
Stability of the pontoon.
Solution:

Result:
GM is positive, the pontoon is stable in its floatation in vertical axis.
Example - 102
Show that a uniform circular cyclinder of SP.gr = 1/3 cannot be in stable equilibrium when floating upright in water when its length exceeds 3/4 of its diameter.
Solution:
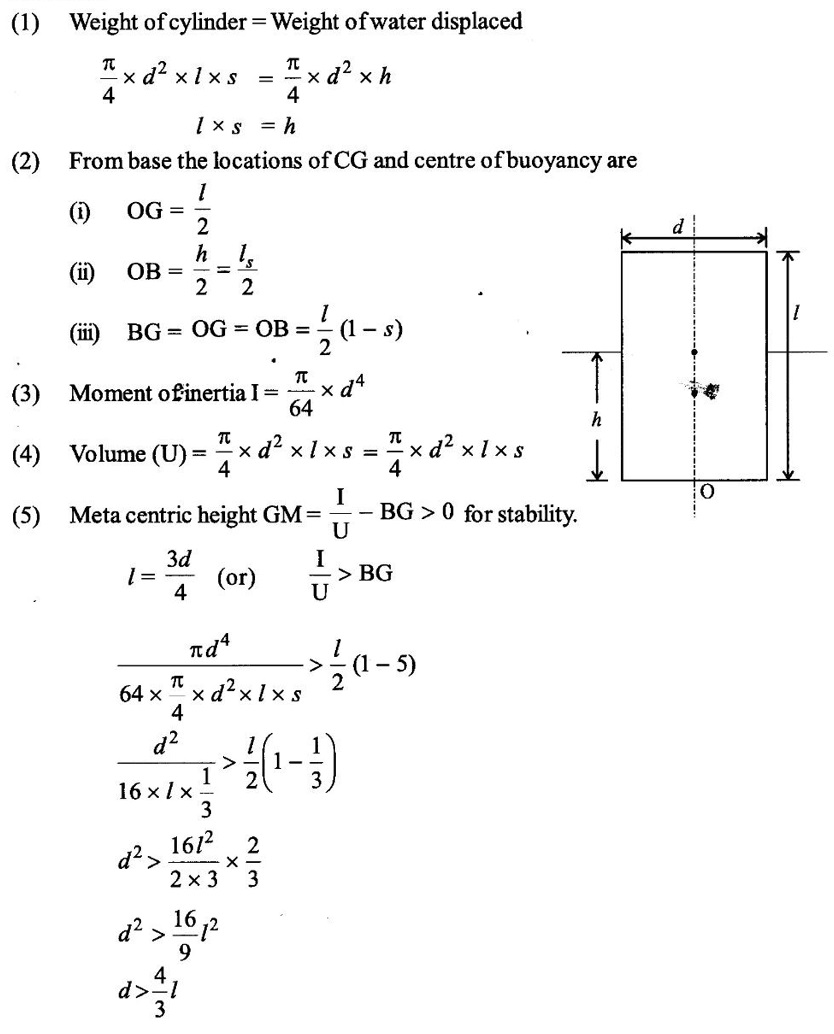
No comments:
Post a Comment