Stability of a Floating Body

 The stability of a floating body is determined by the relative position of the centre of gravity, and the meta centre M of the body.

STABILITY OF A FLOATING BODY

The stability of a floating body is determined by the relative position of the centre of gravity, and the meta centre M of the body. If G is located below M, the floating body remains in stable equilibrium. If G is above M, the body is in unstable equilibrium. If G coincides with M, the body is in neutral equilibrium.

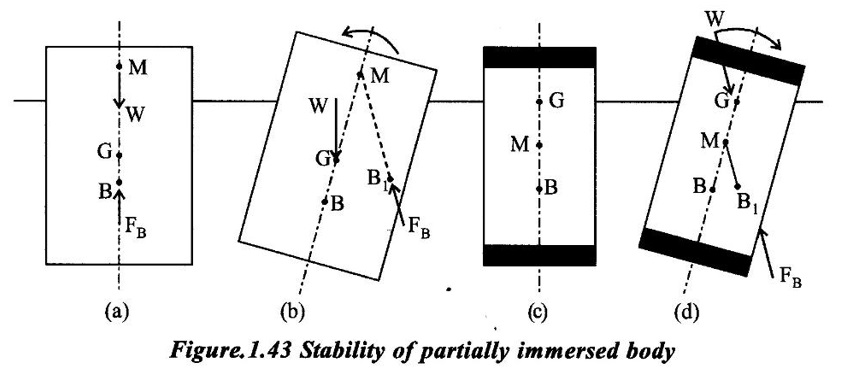
Consider partially immersed body floating in a liquid which is initially in equilibrium with FB = w. The centre of gravity is below meta-centre of the body as shown in figure 1.43 (a) and (b).

If a slight clockwise angular displacement is given to the body, the centre of buoyancy B shifts to new position B1 such that the vertical line through B1 intersects axis at M. The weight W acting at G and the buoyant force FB acting at B1 constitute an anticlockwise couple as shown in figure 1.43 (b), which will bring back the body to its original position. Thus at this condition, the floating body is in stable equilibrium.

Now, consider the case in which the centre of gravity is above in which the centre of gravity is above meta-centre as shown in figure 1.43 (c) for a small clockwise angular displacement B shifts to B1 with the vertical through B1 passing through M, as shown in figure 1.43 (d). In the new passion the restoring couple also acts in the clockwise direction, thus overturning the floating body. At this direction, condition, the floating body is said to be in equilibrium.

If for the floating body G coincides with M, there will be neither a restoring couple not an overturning couple developed when the body is slightly tilted. The body will adapt to the new position and hence is said to be in neutral equilibrium.