Solved Problems on Pascals Law

 Solved Problems on Pascals law: Fluid Properties and Flow Characteristics - Fluid Mechanics and Machinery

Solved Problems on Pascals law

Example - 52

The diameters of ram and plunger of an hydraulic press are 180 mm and 28 mm respectively. Find the weight lifted by the hydraulic press when the force applied at the plunger is 380 N.

Given data:

Diameter of ram D= 180 mm = 0.18 m

Diameter of plunger d = 28 mm = 0.028 m

Force on the plunger (F) = 380 N.

To find:

Weight (W) = ?

Solution:

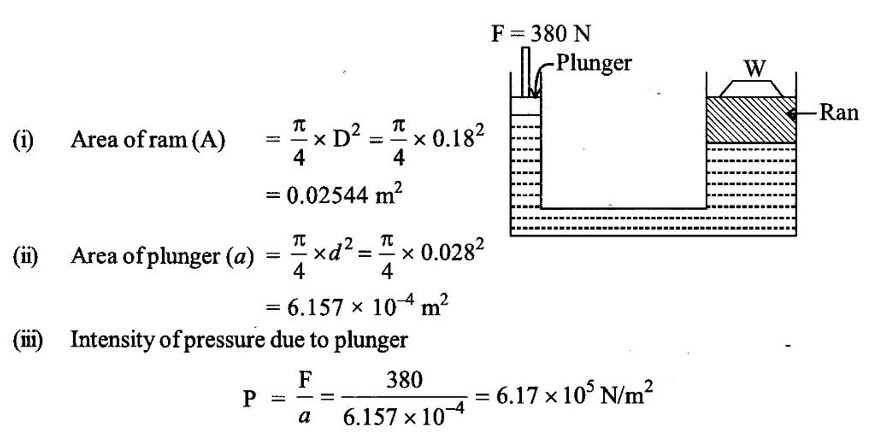
In pascals law the intensity of pressure will be equally transmitted.

Result:

Weight lifted by hydraulic press W = 15.699 × 103 N

W = 15.699 KN

Example - 53

For the hydraulic Jack as shown in figure, find the load lifted by the large piston when a force of 350 N is applied on the small piston. Assume the specific weight of the liquid in the Jack is 9810 N/m3.

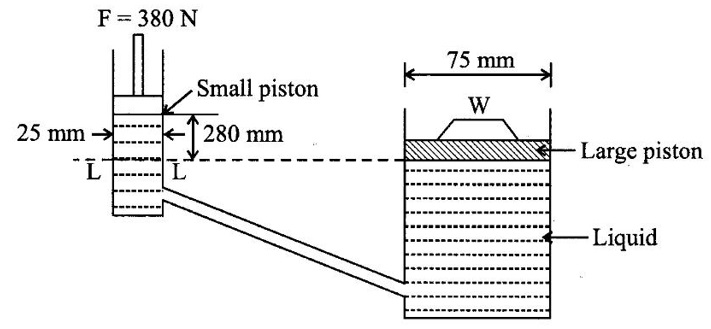
Given data:

Force (F) = 350 N

Ram diameter = 75 mm = 0.075 m

Piston diameter = 25 mm = 0.025 m

To find:

Load lifted (W)

Solution:

Result:

Load lifted (W) = 3.16 KN.

Example - 54

Find the depth of oil of specific gravity of 0.82 which produces an intensity of pressure equal to 2.5 KN/m2. Also find the pressure head in terms of water and mercury.

Given data:

Specific gravity of oil (S) = 0.82 

Intensity of pressure (P) = 2.5 KN/m2

To find:

Pressure head (h)

Solution:

Density of oil (loil) = specific gravity of oil × density of water

= 0.82 × 1000 = 820 kg/m2.

Intensity of pressure (P) = 2.5 KN/m2 = 2.5 × 1000 N/m2

= 2500 N/m2

Now intensity of pressure

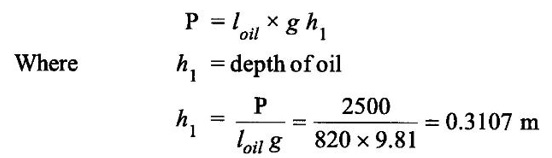
Now assume h2 and h3 are the pressure heads of water and mercury respectively of same intensity of pressure (p).

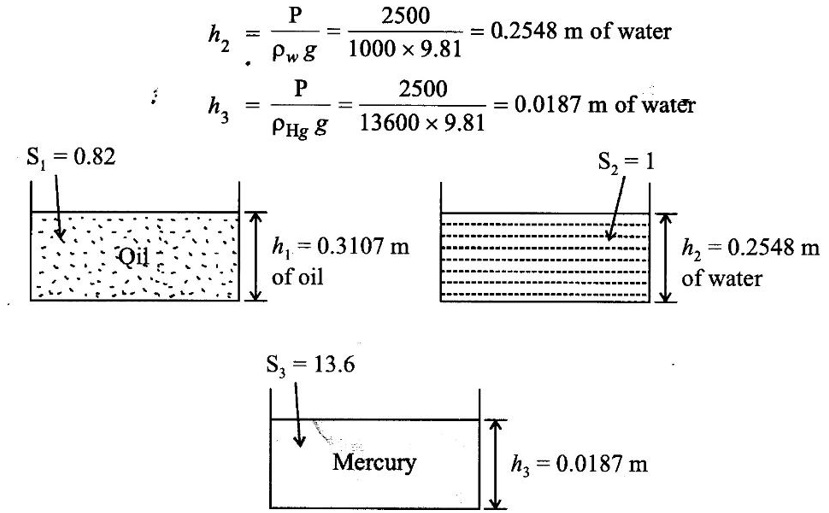Result:

(i) Pressure head h1 = 0.3107 m of oil

(ii) Pressure head h2 = 0.2548 m of water

(iii) Pressure head h3 = 0.0187 m of Hg.

Example - 55

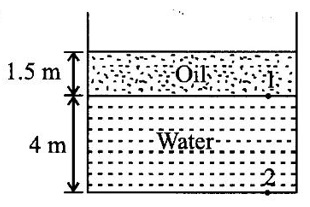
An open tank contains water upto a depth of 4m and above it an oil of specific gravity 0.9 for a depth of 1.5m. Find the intensity of pressure.

(i) At the interface of the two liquids

(ii) At the bottom of the tank.

Given data:

Height of water h1 = 4 m

Height of oil h2 = 1.5 m

Specific gravity of all s1 = 0.9

To find:

Pressure intensity at interface at point 1 and 2.

Solution:

case (i) pressure intensity at the interface of the two liquids at point 1 

P1 = ρ g h2 = 900 × 9.81 × 1.5

= 13243.5 N/m

P1 = 13.243 Kpa

case (ii) pressure intensity at the bottom @point 2

P2 = (ρ g h2)oil + (ρ g h1)water

= P1 + (egh1)water

= 13243.5 + (1000 × 9.81 × 4)

= 52483.5 N/m2

P2 = 52.48 KPa

Result:

(i) Pressure at the interface of the two liquids = 13.243 KPa

(ii) Pressure at the bottom = 52.48 KPa

Example - 56

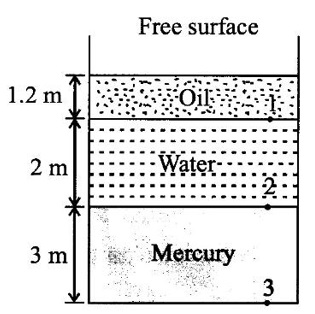
An open tank contains mercury upto a depth 4m and above of water upto a depth 2m and above water an oil of specific gravity 0.92 for a depth of 1.2 m. Find the intensity of pressure

 (i) At the interface of the oil and water 

(ii) At the interface of water and mercury 

(iii) At the bottom of the tank

Given data:

Height of mercury h1 = 3m

Height of water h2 = 2m

Height of oil (h3) = 1.2 m

Specific gravity of oil (soil) = 0.92

To find:

(i) Pressure at interface of oil and water (@point 1)

(ii) Pressure at interface of water and mercury (@point 2)

(iii) Pressure at the bottom of the tank (@point 3)

Solution:

case (i) Pressure at interface of oil and water

P1 = (ρ g h3)oil

= 920 × 9.81 × 1.2

= 10830.24 N/m2

P1 = 10.83 KPa

case (ii) Pressure at interface of water and mercury

P2 = (ρ g h3)oil + (ρ g h2)water

= P1 + (1000 × 9.81 × 2)

= 10830.24 + 19620

= 30,450.24 N/m2

P2 = 30.45 KPa

case (iii) Pressure at the bottom of the tank

P3 = (ρ g h3)oil + (ρ g h2)water + (ρ g h1)Hg

= P2 + (ρ g h1)Hg

= 30.45 + (13600 × 9.81 × 3)

= 30.45 + 400248

= 430698.24 N/m2

P3 = 430.69 KPa

Result:

(i) Pressure at the interface of oil and water 10.83 KPa

(ii) Pressure at the interface of water and mercury = 30.45 KPa

(iii) Pressure at the bottom of tank = 430.69 KPa

Example - 57

The diameter of a small piston a larger piston of a hydraulic Jack are 40 mm 200 mm respectively. A force of 500 N is applied on the small piston. Find the load lifter by the larger piston when

(i) The pistons are at the same level

(ii) Small piston is 500 mm above the large piston

Specific gravity of oil in the Jack is 0.92.

Given data:

Diameter of small piston (d) = 40 mm = 0.04 m

Diameter of large piston (D) = 200 mm = 0.2 m

Force (F) = 500 N

Specific gravity of oil s1 = 0.92

To find:

(i) Load (W) when the pistons are at the same level

(ii) Load (W) when small piston is 500 mm above the large piston

Solution:

Density of oil (ρ) = 920 kg/m2

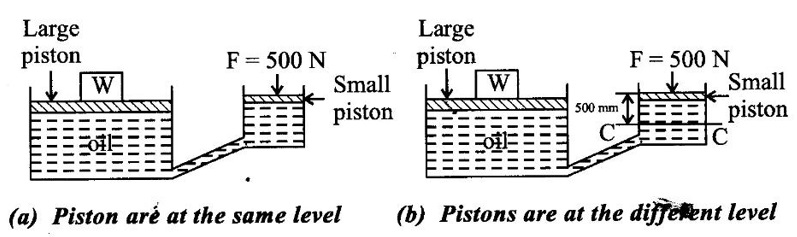
Case (i) when the pistons are at the same level

W W = 5.334 KN

Case (ii) when the small piston is 500 mm above the large piston

P = intensity of downward pressure at C-C level

= intensity of pressure due to 500 N + intensity of pressure due to 500 mm oil head.

Result:

(i) Load when the pistons are at the same level,

W = 5.334 KN

(ii) Load when the pistons is 500 mm above the large piston

W = 5.394 KN