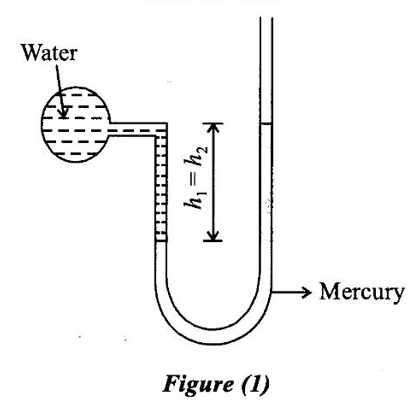
Solved Problem on Manometers

 solved problem on manometers: Fluid Properties and Flow Characteristics - Fluid Mechanics and Machinery

SOLVED PROBLEM ON MANOMETERS

Example - 58

A U-tube manometer is used to measure the pressure of oil of specific gravity 0.95 flowing in a pipe line. Its left end is connected to the pipe and the right limb is open to atmosphere. The centre of the pipe is 110 mm below the level of mercury in right limb. If the difference of meucury level in the two limbs is 170 mm. Determine the absolute pressure of the oil in the pipe. 

Given data:

SP. gravity of oil s1 = 0.95

SP. gravity of mercury s2 = 13.6 (taken constant value)

Oil height in left limb h1 = 170 - 110 = 60 mm

Mercury height in right limb h2 = 170 mm

(above X - X datum line) = 0.17 m

To find:

Absolute pressure of oil in the pipe line.

Solution:

Given manometer is simple U-tube manometer in positive pressure gauge type. 

(i) Difference of pressure head = h2 s2 - h1 s1

= 0.17 × 13.6 – 0.06 × 0.95

= 2.312 - 0.057

h = 2.255 m.foil

(ii) Specific weight of oil (W) = s1 × SP. weight of water

= 0.95 × 9810

W = 9319.5 N/m3

(iii) Pressure (P) = W × h

= 9319.5 × 2.255 = 21.015 × 103 N/m2

Pgauge = 21.015 KN/m2

(iv) Absolute pressure Pabs = Pgauge + Patm

= 21.015+ 101.013

Pabs = 122.02 KN/m2

Result:

Absolute pressure of oil Pabs = 122.02 KN/m2

Example - 59

U-tube manometer containing mercury was used to find the negative pressure in the pipe, containing water. The right limb was open to the atmosphere. Find the vacuum pressure in the pipe, if the difference of mercury level in the two limbs was 110 mm and height of water in the left limb from the centre of the pipe was found to be 50 mm below.

Given data:

Height of water level inleft limb (h1) = 50 mm

(above X-X Datum lines) = 0.05 m

Height of mercury level in right limb h2 = 110 mm

(above X-X Datum line) = 0.11 m

To find:

Vaccum pressure in the pipe.

Solution:

(i) SP. gravity of water s1 = 1

(ii) SP. gravity of mercury = 13.6

(iii) Difference of pressure head (h) = − (h1 s1 + h2 s2)

= -(0.05 × 1 + 0.11 × 13.6)

h = -1.546 m of water

(iv) Vacuum pressure Pvac = W × h = 9810 × -1.546 - 15.166 KN/m2

Result:

Vacuum pressure Pvac = -15.166 KN/m2

Example - 60

A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The right limb of the manometer contains mercury and is open to atmospheric the contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tube is 10 cm and the free surface of mercury is in level with the centre of the pipe. If the pressure of water in page line is reduced to 9810 N/m2, calculate the new difference in the level of mercury.

Given data:

Difference head (h) = 10 cm

= 0.1 m

To find:

Case I - find the pressure of pipe

Case II - the new difference head when pressure reduced to 9810 N/m2.

Solution:

Case - I:

(i) SP. gravity of water s1 = 1

(ii) SP. gravity of mercury s2 = 13.6

(iii) Difference of head h = h2 s2 - h1 s1 (h1 = h2)

= h1 s2 = h1 s1 

= h1 (s2 – s1)

= 0.1 (13.6 - 1)

= 1.26 of water

(iv) Pressure of pipe P = W × h

= 9810 × 1.26

= 12360.6 N/m2

Case - II

(i) Pressure P = W × h

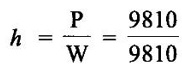
h = 1 m of water

(ii) Difference of head h = (h2 - 2x)s2 - (h1 − x)s1

= (0.1 - 2x)13.6 - (0.1 − x)1

Result:

Case - I : Pressure of pipe P = 12360.6 N/m2

Case II: New difference of head (h) = 0.08016 m of water

Example - 61

A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The right limb of the manometer contains mercury and is open to atmospheric. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tube is 20 cm and the free surface of mercury is in level with the centre of the pipe. If the pressure of water in pipe line is increased to 50%. Calculate the new difference in the level of mercury.

Given data:

Difference of head (h) = 20 cm = 0.2 m

To find:

Case - I

Pressure of pipe.

Case - II

New difference head when pressure is increased in 50%.

Solution:

(iv) New difference of head h = h + x

= 0.2 + (0.048)

= 0.248 m of water

Result:

(i) Pressure (P) = 24721.2 N/m2

(ii) Difference of head (h) = 0.248 on of water.

Example - 62

Figure shows a single column manometer connected to a pipe containing liquid of specific gravity 0.8. The ratio of area of the reset unit to that of the limb is 110. Find the pressure in the pipe. Take SP.gravity of mercury = 13.6. 

Given data:

Liquid specific gravity s1 = 0.8

Mercury SP gravity s2 = 13.6

To find:

Pressure in the pipe.

Solution:

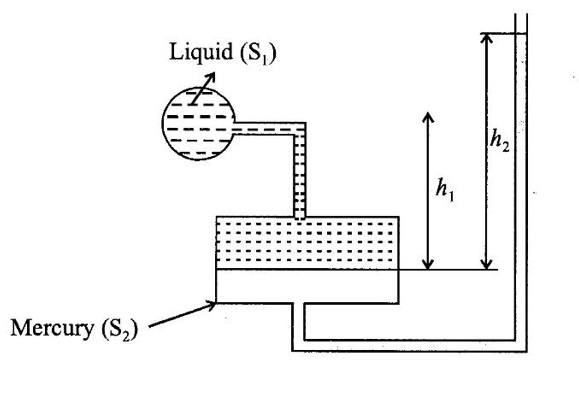(i) Height of the liquid in left limb h1 = 300 mm = 0.3 m

(ii) Height of the mercury in right limb h2 = 500 mm = 0.5 m

(iii) Pressure head h = a/A h2 (s2 − s1) + h2 s2 – h1 s1

= 1/110 × 0.5 (13.6 - 0.8) + 0.5 × 13.6 – 0.3 × 0.8

= 0.058 + 6.8 - 0.24

= 6.618 m of water

(iv) Pressure (P) = W × h

= 9810 × 6.618

P = 64922.58 N/m2

Result:

Pressure of pipe (P) = 64922.58 N/m2.

Example - 63

A manometer consists of an inclined glass tube which is connected to a pipe line. The liquid contained in a reservoir is mercury and the pipe oil of specific gravity is 0.95. The slope of the tube is 2 horizontal to 1 vertical. The diameters of the reservoir and tube are 60 mm and 6mm respectively. The length of mercury moved in right limb along the pipe is 55 cm. Calculate the pressure in the limb. 

Given data:

SP. gravity of oil s1 = 0.95

SP. gravity of mercury s2 = 13.6

Slope of the tube 2:1

Diameter of pipe d = 6 mm = 0.006 m

Diameter of resetvoit D = 60 mm = 0.06 m

Length of the tube l = 55 cm = 0.55 m

To find:

Pressure of the pipe.

Solution:

(i) Slope of the tube 2:1

tan θ = 1/2 = 0.5 

θ = tan-1 (0.5)

θ = 26.56°

(ii) Height of marcury in right limb h2 = l × sin θ

= 0.55 × sin 26.56

h2 = 0.2459 m

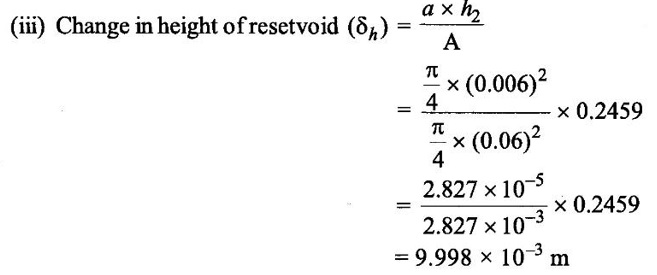(iv) Height of liquid in left limb h1 = h2 - δh

= 0.2459 - 2.458 × 10-3

h1 = 0.243 m

(v) Difference of head h = h2 s2 – h1 s1

= 0.2459 × 13.6 – 0.243 × 0.95

= 3.344 - 0.23085

h = 3.113 m

(vi) Pressure (P) W × h

= 9810 × 3.113

P = 30.54 × 103 N/m2

Result:

Pressure (P) = 30.54 × 103 N/m2

Example - 64

A differential manometer contains mercury and is connected to pipes A and B as shown in figure the pipe A contains a liquid of specific gravity 1.5 and the of the pipe B contains an of SP. gravity 0.85. If the pressure head difference between the two pipes is 10 m of water. Find the difference of mercury level? 

Given data:

SP. gravity of liquid of pipe As1 = 1.5

SP. gravity of liquid of pipe B s2 = 0.85

Pressure head difference (ρA – ρB) = 10 m

Height of centre of pipe to mercury level in tight limb h1 = 3 m

To find:

Difference of mercury level (h)

Solution:

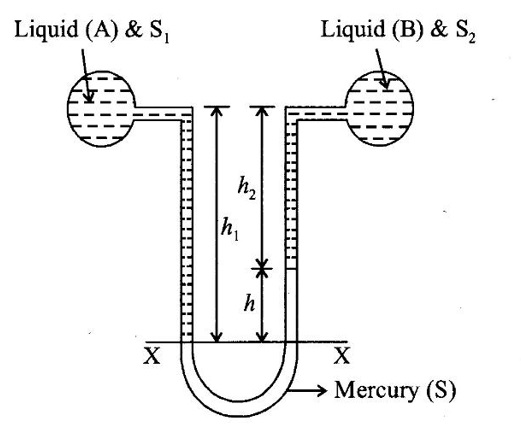
(i) Pressure head in left limb above X-X Datum line

= h1 s1 + hA [h1 = h + h2] 

= (h + h2) s1 + hA

= (h s1 + h2 s1 + hA

(ii) Pressure head in Right limb above X-X Datum line = hs + h1 s2 + hB

(iii) Equating the above Equation pressure head left limb = Pressure head right limb.

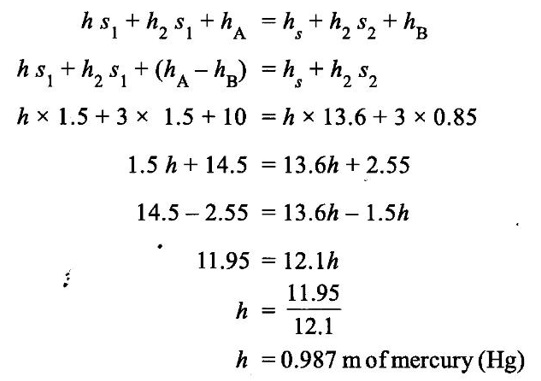
Result:

Difference of mercury level h = 0.987 mm of Hg.

Example - 65

A differential manometer connected at the two points A and B in a pipe containing an oil of specific gravity of 0.9 shows a difference in mercury levels of 160 mm. Find the difference in pressure of the two points.

Given data:

SP. gravity of oil s1 = 0.9

SP. gravity of mercury = 13.6

Difference of mercury levels h = 160 mm

= 0.16 m

Solution:

(i) Difference of pressure head (hA - hB)

= hs + h2 s2 - h s1 - h2 s1         [s2 = s1]

= hs + h2 s2 - h s1 - h2 s2        

= hs - h s1 

= h(s - s1)

= 0.16 (13.6 - 0.9)

(hA - hB) = 2.032 m of oil.

(ii) Difference of pressure (PA - PB) = W × (hA - hB)

SP. weight of oil (W) = SP. weight of water × SP. gravity of oil.

= 9810 × 0.9

W = 8829 N/m2

PA - PB = 8829 × 2.032

= 17940.528 N/m2

Result:

Pressure difference (PA - PB) = 17940.528 N/m2 

Example – 66

Figure shows a U-tube differential manometer connecting two pressure pipes at A and B. The pipe A contains a liquid of specific gravity 1.5 under a pressure of 100 KN/m2. The pipe B contains oil of specific gravity 0.9 under a pressure of 210 KN/m2. Find the difference of pressure measured by mercury as fluid filling U-tube.

Given data:

SP. gravity of liquid A, s1 = 1.5

SP. gravity of liquid B, s2 = 0.9

Pressure at A (PA) = 100 KN/m2

Pressure at B (PB) = 210 KN/m2

To find:

Difference of mercury level.

Solution:

(i) Pressure head at A1, hA = PA/W

S.P weight of liquid A = SP. weight of water × SP. gravity liquid A

= 9810 × 1.5

= 14715 N/m

WA = 14.715 KN/m3

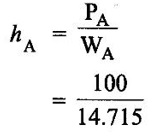
hA = 6.795 m of liquid

(ii) SP. weight of liquid BSP weight of water × SP gravity of liquid B

= 9810 × 0.9

= 8829 N/m2

WB = 8.829 KN/m3

(iii) Pressure head at B, hB = PB/WB

= 210/8.829

hB = 23.78 m of liquid.

(iv) Pressure head above (X-X) in the left limb

= hs + h1 s1 + hA

(v) Pressure head above (X-X) in the tight limb

= h2s2 + hB

(vi) Equating above two Equations

hs + h1 s1 + hA = h2s2 + hB (h2 = h + 1.0)

h × 13.6 + 3.6 × 1.5 + 6.795 = (h + 1.0) × 0.9 + 23.78

13.6h + 5.4 + 6.795 = 0.9h + 0.09 + 23.78

13.6h + 5.4 + 6.795 = 0.9 h + 0.09 + 23.78 

13.6h - 0.9h - 0.09 + 23.78 − (5.4 + 6.795)

12.7 h = 11.675

h = 11.675 / 12.7

h = 0.919 m of mercury

Result:

Difference of mercury level h = 0.919 m of mercury.

Example - 67

Figure shows a differential manometer connected at two points A and B pressure of water at A is 110 KN/m2. Find the absolute pressure at B.

Given data:

Pressure of water at A1 PA = 110 KN/m2

SP. gravity of oil s2 = 0.95

SP. gravity of water s1 = 1

Pressure head of water h1 = 700 mm = 0.7 m

Pressure head of oil h2 = 300 mm

= 0.3 m

Difference of mercury level h = 175 mm

= 0.175 m

To find:

Absolute pressure B, PB1

Solution:

(iv) Equating above two equations

h1 s1 + hA = hs + h2 s2 + hB

0.7 × 1 + 11.21 = 0.175 × 13.6 + 0.3 × 0.95 + hB

11.91 = 2.38 + 0.285 + hB

= 2.665 + hB

hB = 11.91 - 2.665

hB = 9.245 m of oil.

(v) Pressure at B, PB = WB × hB

SP. weight of oil WB = SP. weight of water × SP gravity of oil = 9810 × 0.95

WB = 9319.5 N/m2

PB = 9319.5 × 9.245 = 86158.77 KN/m2

= 86.158 KN/m2

Result:

Absolute pressure at B, PB = 86.158 KN/m2

Example - 68

The below figure shows an inverted differential manometer having an oil of specific gravity 0.9 connected to two different pipes carrying water under pressure. Determine the pressure in the pipe B. The pressure in pipe A is 3.0 metres of water.

Given data:

Height of water in left limb (h1) = 300 mm

= 0.3 m

Height of water in tight limb (h2) = 100 mm

= 0.1 m

Pressure in pipe A, hA = 3.0 m of water

SP gravity of liquid s = 0.9

To find:

Pressure in the pipe B.

Solution:

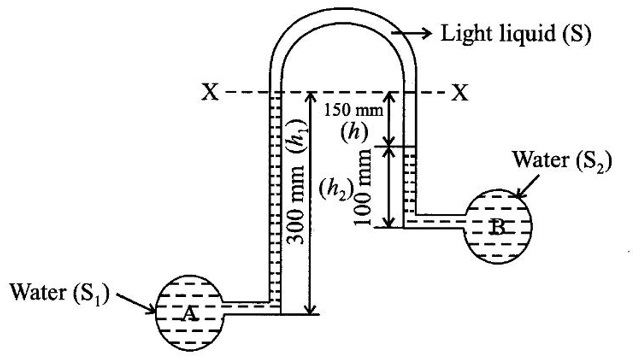
Pressure head in left limb = hA - h1s1

= 3 0.3 × 1

(ii) Pressure head in right limb = hB - h2 - hs

= hB - 0.1 × 1 - 0.15 × 0.9 

= hB - 0.235

(iii) Equating the above equ

2.7 = hB - 0.235

hB = 2.7 + 0.235

hB = 2.935 m of water

(iv) Pressure PB = W × hB

= 9810 × 2.935

PB = 28.789 KN/m2

Result:

Pressure in the pipe B, PB = 28.789 KN/m2

Example - 69

An inverted differential manometer is connected to two pipes A and B carrying water under pressure as shown in figure. The fluid in the manometer is oil of specific gravity 0.85. Determine the pressure difference between A and B. 

Given data:

Specific gravity of oil s = 0.85.

To find: 

Pressure difference (PB - PA).

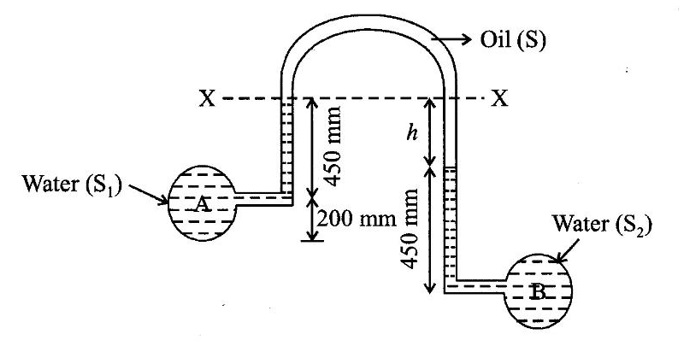
Solution:

(i) Difference of pressure head (h) = (0.45 + 0.2) - 0.45

h = 0.2 m

(ii) Pressure head in left limb below (X – X)

= hA - h1s2

= hA - 0.45 × 1

= hA – 0.45

(iii) Pressure head in right limb below (X–X)

= hB - h2s2 - hs

= hB - 0.45 × 1 - 0.2 × 0.85

= hB - 0.45 - 0.17

= hB - 0.62

(iv) Equating above Equation

hA - 0.45 = hB -  0.62

hB - hA = 0.62 - 0.45

hB - hA = 0.17 m of water

(v) Difference of pressure head (PB - РA ̧) = (hB - hA) × W

= 0.17 × 9810

(PB - РA) = 1667.7 N/m2.

Result:

Difference of pressure (PB - РA) = 1667.7 N/m2.