University Solved Problems

 Stress, Strain and Deformation of Solids - Strength of Materials: University solved problems

UNIVERSITY SOLVED PROBLEMS

Example 1.75: 

A rectangular block of material is subjected to a tensile stress of 110 N/mm2 on one plane and a tensile of 47 N/mm2 on a plane at right angles to the former. Each of the above stresses is accompanies by a shear stress of 63 N/mm2. Determine the principal stresses, principal planes and the maximum shear stress.

Given:

σ1 = 110 N/mm2

σ2 = 47 N/mm2

q = 63 N/mm2

To find: 

Principal stresses, principal plane and maximum shear stress.

Solution: 

= 70.43 N/mm2

Results:

Major principal stress, σnl = 148.9 N/mm2

Minor principal stress, σn2 = 8.06 N/mm2

Principal plane, θ = 31.71° or 121.71°

Maximum shear stress, (σt)max = 70.43 N/mm2

Example 1.76:

The stresses at a point in a strained material is Px = 200 N/mm2 and py = -150 N/mm2 and q = 80 N/mm2. Find the principal plane and principal stresses. Using graphical method and verify with analytical method.

Given:

px = σ1 = 200 N/mm2

py = σ2 = -150 N/mm2

q = 80 N/mm2

To find: 

Principal stresses & Principal plane

Solution: 

Graphical method:

1. Draw a horizontal line and set off OA and OB equal to σ, and σ2 on opposite sides to the scale, since both the stresses are opposite to each other.

2. Bisect BA at C.

3. Draw perpendicular line AS from A which is equal to hear stress. 80 N/mm2 and to the same scale draw BR from B.

4. With C as centre and CS as radius draw a circle. This is known as Mohr's circle.

5. By measurement, we find

Major principal stress, σnl = OH = 215 N/mm2

Minor principal stress, σn2 = OG = -165 N/mm2

Analytical method:

= 217.4 N/mm2

Results: 

From the above two methods we found that both the answers were very close to each other.

Major principal stress,σnl = 217.4 N/mm2

Minor principal stress, σn2 = - 167.4 N/mm2

Location of principal plane, θ = 12.28° or 102.28°

Example 1.77: 

A rectangular block of material is subjected to a tensile stress of 90 N/mm2 along x-axis and a compressive stress of 45 N/mm2 on a plane at right angles to it, together with shear stresses of 80 N/mm2 on the same plane calculate 

1. The direction of principal planes

2. The magnitude of principal stresses

3. The magnitude of the greatest shear stress

Given:

σ1 = 90 N/mm2

σ2 = -45 N/mm2

q = 80 N/mm2

To find: 

1. Direction of principal planes

2. The magnitude of principal stresses 

3. The magnitude of greatest shear stress

Solution:

Results:

1. The direction of principal plane, θ = 24.9° or 114.9°

2. Major principal stress, σn1 = 127.17 N/mm2

3. Minor principal stress, σn2 = -82.17 N/mm2

4. The magnitude of greatest shear stress, (σt)max = 104.67 N/mm2

Example 1.78: 

Two planes AB and AC which are right angles carry shear stress of intensity 17.5 N/mm2 while these planes also carry a tensile stress of 70 N/mm2 and a compressive stress of 35 N/mm2 respectively.

Determine the principal planes and the principal stresses. Also determine the maximum shear stress and planes on which it acts. 

Given:

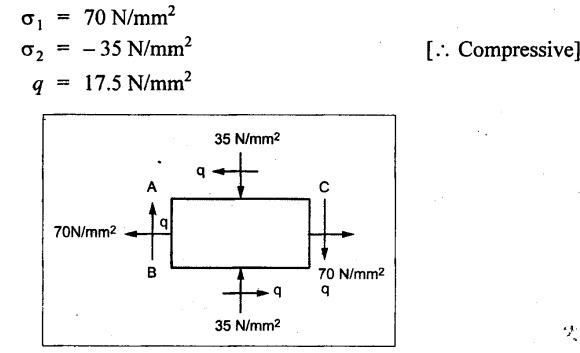
To find: 

1. Principal planes and principal stresses

2. Maximum shear stress & plane

Solution:

Results:

Principal plane, θ = 9.217° or 99.217°

Major principal stress, σnl = 72.83 N/mm2

Minor principal stress, σn2 = = -37.83 N/mm2

Maximum shear stress (σt)max = 55.33 N/mm2

Direction of maximum shear stress, θ = -35.78°

Example 1.79: 

The state of stress at a plane are given by σxx = 20 MPa, σyy = 20 MPa, τxy = 40 MPa. Find the principal stresses, principal planes and maximum shear stress also its plane. 

[Same as previous problem (1.78). Take σ1 = 20 MPa = 20 N/mm2, σ2 = 20 MPa = 20 N/mm2, qxy = 40 MPa = 40 N/mm2]

Example 1.80 :

An element has a tensile stress of 600 N/mm2 acting on two mutually perpendicular planes and shear stress of 100 N/mm2 on these planes. Find the principal stress and maximum shear stress. 

Given Data:

σ1 = 600 N/mm2

σ2 = 100 N/mm2

To find: 

Principal stresses and maximum shear stress.

Solution: 

Principal Stresses:

= 100 N/mm2

Results:

Major principal stress, σnl = 700 N/mm2

Minor principal stress, σn2 = 500 N/mm2

Maximum shear stress, (σt)max = 100 N/mm2

Example 1.81: 

At a certain point in a strained material, the stresses on two planes at right angles to each other are 80 MN/m2 and 60 MN/m2 both tensile. They are accomplished by a shear stress of 20 MN/m2. Find the location of principal planes and evaluate the principal stresses. 

Given: 

σ1 = 80 MN/m2

σ2 = 60 MN/m2

q = 20 MN/m2

To find: 

1. Location of principal plane

2. Principal stresses.

Solution: 

Position of principal plane

Results: 

Position of principal planes are 31.7° or 121.7°

Major principal stress, σnl = 92.36 MN/m2

Minor principal stress, σn2 = 47.63 MN/m2

Example 1.82: 

A rectangular block of material is subjected to tensile stress of 110 N/mm2 on the plane and a compressive stress of 45 N/mm2 on the plane at right angles to the former. Each of the above stresses are accompanied by a shear stress of 60 N/mm2 and that associated with the former tensile stress tends to rotate the block anticlockwise. Find the principal stresses and principal planes.

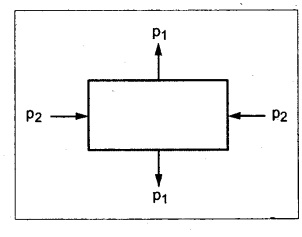
Given:

σ1 = 110 N/mm2

σ2 = -45 N/mm2 (⸫ compressive)

q = 60 N/mm2

To find: 

1. Principal stresses

2. Principal planes

Solution:

Results: 

Major principal stress, σnl = 130.5 N/mm2

Minor principal stress, σn2 = -65.5 N/mm2

Principal planes are located at 18.87° or 108.87°

Example 1.83:

At a point in a strained material, the principal stresses are 100 N/mm2 tensile and 60 N/mm2 compressive. Calculate the normal stress, shear stress and resultant stresses on a plane inclined at 50° to the axis of the major principal stress.

Given:

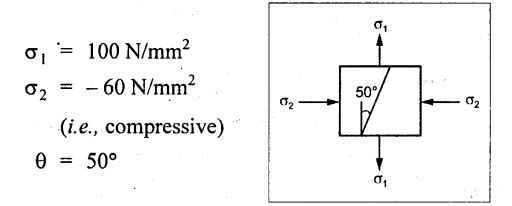
To find: 

Normal stress, shear stress and resultant stress on 50° inclined plane.

Solution:

Results:

Normal stress, σn = 6.108 N/mm2

Shear stress, σt = 78.78 N/mm2

Resultant stress, σres = 79.02 N/mm2

Example 1.84:

At a point in a strained material, the principal stresses are 150 N/mm2 (tensile) and 60 N/mm2 (compressive). Determine the resultant stress in magnitude and direction on a plane inclined at 45° to the axis of the major principal stress. What is the maximum intensity of shear stress in the material at the point? 

Given:

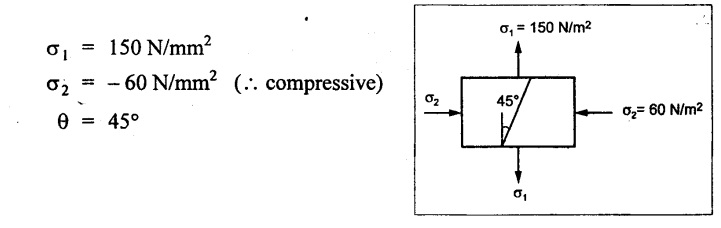
To find: 

1. Resultant stress, and

2. Maximum shear stress.

Solution:

Results:

1. Resultant stress, σres = 114.23 N/mm2

2. Maximum shear stress, (σt)max = 105 N/mm2

Example 1.85 :

A point in a strained material is subjected to mutually perpendicular stresses of 600 N/mm2 (tensile) and 400 N/mm2 (compressive). It is also subjected to a shear stress of 100 N/mm2. Draw Mohr's circle and find the principal stress and maximum shear stress.

Given:

σ1 = 600 N/mm2 (Tensile)

σ2 = - 400 N/mm2 (Compressive)

q = 100 N/mm2

To find: 

From Mohr's circle,

1. Principal stresses

2. Maximum shear stress

Solution:

1. Draw a horizontal line and set off OA and OB equal to 600 N/mm2 and 400 N/mm2 on the opposite side to some scale, since both stresses are opposite side to each other.

2. Bisect BA. at C

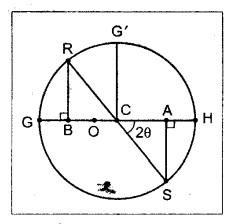
3. Draw perpendicular line AS or RB which is equal to shear stress 100 N/mm2 to the same scale.

4. With C as centre and CS-as radius, draw a circle. This is known as Mohr's circle.

5. Draw a line CG' perpendicular to AB, which will gives the maximum shear stress value.

By measurement,

Major principal stress, σnl = OH = 610 N/mm2 

Minor principal stress, σn2 = OG = - 410 N/mm2

Maximum shear stress, (σt)max = CG' = 510 N/mm2

Results:

Major principal stress, σnl = 610 N/mm2

Minor principal stress, σn2 = - 410 N/mm2

Maximum shear stress, (σt)max = 510 N/mm2 

Example 1.86 :

A point is subjected to a tensile stress of 60 N/mm2 and a compressive stress of 40 N/mm2 acting on two mutually perpendicular planes and a shear stress of 10 N/mm2 on these planes. Determine the principal stresses as well as maximum shear stress. Also give the Mohr's circle method for finding the same.

Given:

σ1 = 60 N/mm2

σ2 = - 40 N/mm2

q = 10 N/mm2

To find:

1. Principal stresses

2. Maximum shear stress

Solution:

Mohr's circle method is same as previous problem.

Results:

Major principal stress, σnl = 60.99 N/mm2

Minor principal stress, σn2 = -40.99 N/mm2

Maximum shear stress, (σt)max = 50.99 N/mm2

Example 1.87:

At a point in a strained material, the resultant intensity of stresses across a certain plane is shown in Fig. Evaluate the principle stresses, Maximum shear stress and their corresponding planes with respect to the direction of the normal stress of 60 MPa. 

Given: 

σ = 60 MPa = 60 N/mm2

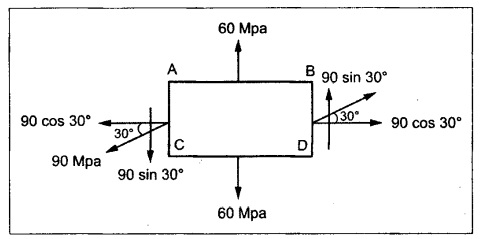
To find: 

1. Principal stresses

2. Maximum shear stress

3. Principal planes with 60 MPa stress direction.

Solution: 

We can resolve the stress 90 MPa which is 30° to the horizontal in to two components.

Results: 

Major principal stress, σnl = 114.85 N/mm2

Minor principal stress, σnl = 23.08 N/mm2

Maximum shear stress, (σt)max = 45.88 N/mm2

Principal planes are located 39° 36′ or 129° 36' with 60 MPa stress direction.

Example 1.88 :

At a point in strained material the resultant intensity of stress across the horizontal plane is 80 √2 MPa tensile inclined at 44° clockwise to its normal. The normal component the intensity of stress across the vertical plane is 20 MPa compressive. Locate the principle planes and find the stresses across them. 

Given:

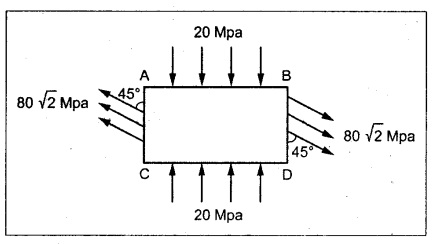
To find:

1. Locate principal planes

2. Principal stresses

Solution: 

We can resolve the given stress 80√2 MPa inclined at 45° to the horizontal in to two components.

(i) Stress normal to section AC & BD and

(ii) Shear stress vertically downward to section AB & CD,

Results:

Location of the principal stress, θ = 28.99° or 118.99°

Major principal stress, σnl = 124.33 N/mm2

Minor principal stress, σn2 = - 64.33 N/mm2