Two mark Questions and Answers: Stress, Strain and Deformation of Solids - Strength of Materials
TWO MARK QUESTIONS AND ANSWERS
1. Define stress.
When an external force acts on a body, it undergoes deformation and at the same time the body resists deformation. The magnitude of the resisting force is numerically equal to the applied force. This internal resisting force per unit area is called stress.

2. Define strain.
When a body is subjected to an external force, there is some change of dimension in the body. Numerically the strain is equal to the ratio of change in length to the original length of the body.
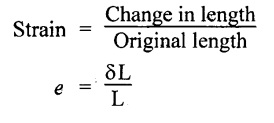
3. State Hooke's law.
It states that when a material is loaded, within its elastic limit, the stress is directly proportional to the strain.

4. Define factor of safety.
It is defined as the ratio of ultimate tensile stress to the permissible stress (working stress).
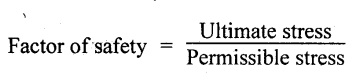
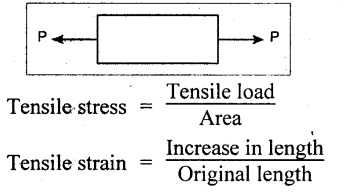
5. State tensile stress and tensile strain.
When a member is subjected to equal and opposite axial pulls, the length of the member is increased. The stress is induced at any cross section of the member is called Tensile Stress and the corresponding strain is known as Tensile Strain.
6. Define compressive stress and compressive strain.
When a member is subjected to equal and opposite pushes as shown in Fig., the length of the member is shortened. The stress produced at any cross section of the member is called compressive stress.
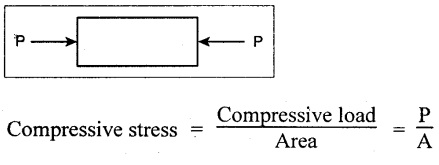
The ratio of decrease in length to the original length is known as compressive strain.
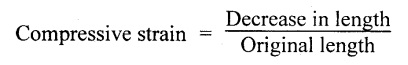
7. Define shear stress and shear strain.
The two equal and opposite forces act tangentially on any cross sectional plane of a body tending to slide one part of the body over the other part. The stress induced in that section is called shear stress and the corresponding strain is known as shear strain.
8. State volumetric strain.
Volumetric strain is defined as the ratio of change in volume to the original volume of the body.
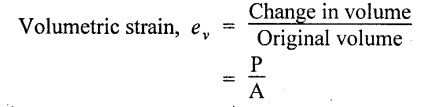
9. Define modulus of elasticity.
When a body is stressed, within its elastic limit, the ratio of tensile stress to the corresponding tensile strain is constant. This ratio is known as Young's modulus.
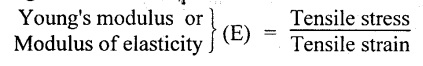
10. Define Modulus of rigidity.
When a body is stressed, within its elastic limit, the ratio of shearing stress to the corresponding shearing strain is constant. This ratio is known as Modulus of rigidity.
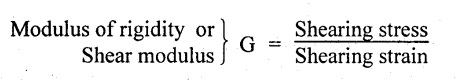
11. State Bulk Modulus.
When a body is stressed, within its elastic limit, the ratio of direct stress to the corresponding volumetric strain is constant. This ratio is known as Bulk Modulus.
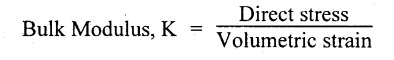
12. Define Poisson's ratio.
When a body is stressed within its elastic limit, the ratio of lateral strain to the longitudinal strain is constant for a given material.
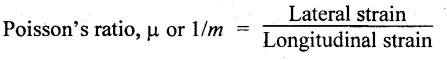
13. State principal plane.
The planes which have no shear stress are known as principal planes. These planes carry only normal stresses.
14. Define principal stresses.
The normal stresses acting on a principal plane are known as principal stresses. law, stress is proportional to strain.
15. According to ―― law, stress is proportional to strain.
Ans. Hooke's law.
16. The Poisson's ratio for a material cannot be more than ――.
Ans. 0.5
17. State the relationship between Young's modulus and Modulus of rigidity.

18. Give the relationship between Bulk modulus and Young's modulus.

19. The principal stress is ―― to the plane and the shear stress is ―― to the plane.
Ans. Normal, Tangential.
20. What do you understand by a compound bar?
A composite member is composed of two or more different materials which are joined together so that the system is elongated or compressed as a single unit.
21. What are the types of elastic constants?
There are three types of elastic constant.
They are,
1. Modulus of Elasticity or young's Modulus, E,
2. Bulk Modulus, K,
3. Shear Modulus or Modulus of Rigidity, G.
22. Write two equations used to find the forces in compound bars made of two materials subjected to tension.

23. What is stability?
The stability may be defined as an ability of a material to withstand high load without major deformation.
24. Define strain energy density.
Strain energy density is defined as the maximum strain energy that can be stored in a material within the elastic limit per unit volume. It is also known as modulus of resilience.
25. Determine the Poisson's ratio and bulk modulus of a material for which A Young's modulus is 1.2 × 105 N/mm2 and modulus of rigidity is 4.8 × 104 N/mm2.
Solution:
We know that,

We know that,

26. Give the relation for change in length of a bar hanging freely under its own weight.
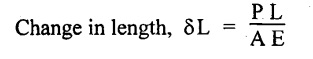
where P → Axial load.
L → Length of the bar.
E → Young's modulus of the bar.
A → Area of the bar
27. A brass rod 2 m long is fixed at both its ends. If the thermal stress is not to exceed 76.5 N/mm2, calculate the temperature through which the rod should be heated. Take the values of a and E as 17 × 10-6/K and 90 GPa respectively.
Solution:
We know that,
Thermal stress, σ = α Τ Ε
⇒ 76.5 = 17 × 10-6 × T × 90 × 103
[⸪ 90GPa = 90 × 109 = 90 × 109 N/m2 = 90 ×103 N/mm2]
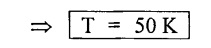
Result:
Temperature, T = 50 K
Two mark Questions and Answers: Stress, Strain and Deformation of Solids - Strength of Materials
TWO MARK QUESTIONS AND ANSWERS
1. Define principal stresses and principal plane.
Principal stress:
The magnitude of normal stress, acting on a principal planes are known as principal stresses.
Principal planes:
The planes which have no shear stress are known as principal planes.
2. On a principal plane, ――― stress is zero.
Ans. Shear stress.
3. The angle between the principal planes and the planes of maximum shear stress is ―――
Ans. 45°
4. The shear stress on a principal planes are ―――
Ans. Zero
5. The angle between the principal planes are ―――
Ans. 90%
6. Give the expression for maximum shear stress in a two dimensional stress system.
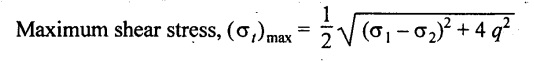
7. What is the radius of Mohr's circle?
Radius of Mohr's circle is equal to the maximum shear stress.
8. A bar of cross sectional area 600 mm2 is subjected to a tensile load of 50 kN applied at each end. Determine the normal stress on a plane inclined at 30° to the direction of loading.
A = 600 mm2
Load, P = 50 kN
θ = 30°
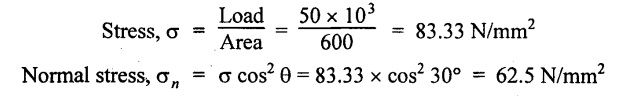
9. Give the expressions for stresses on an inclined plane when it is subjected to a axial pull.
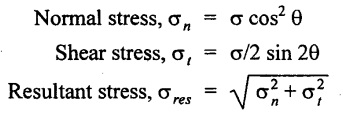
10. What is the use of Mohr's circle?
It is used to find out the normal, tangential, resultant stresses and principal stress and their planes.
11. What are the planes along which the greatest shear stresses occur?
Greatest shear stress occurs at the planes which is inclined at 45° to its normal.
12. Write the expressions for a normal stress on an inclined plane in a block which is subjected to two mutually perpendicular normal stresses and shear stresses?
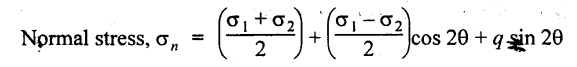
13. At a point in a strained material is subjected to a compressive stress of 100 N/mm2 and shear stress of 60 N/mm2. Determine graphically or otherwise the principal stresses.

14. In case of equal like principal stresses, what is the diameter of the Mohr's circle?
Zero.
15. What is the value of maximum shear stress when the principal stresses are σ1 compression and tension?
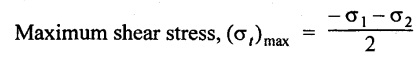
No comments:
Post a Comment