Shear Tests

 There are two main types of test which may be used for the determination of the properties of a material in shear.

SHEAR TESTS

✔ There are two main types of test which may be used for the determination of the properties of a material in shear. They are : 

1. Test performed using a pure shear force↑, and

2. Test performed using the application of a torque to a cylindrical specimen i.e., torsion test.

† Shear force simply means a tangential force.

1. Shear Test Using a Pure Shear Force

✔ Fig.5.17 illustrates the shear test, performed using a pure shear force. In this type, the force is imposed parallel to the upper and lower faces of the body.

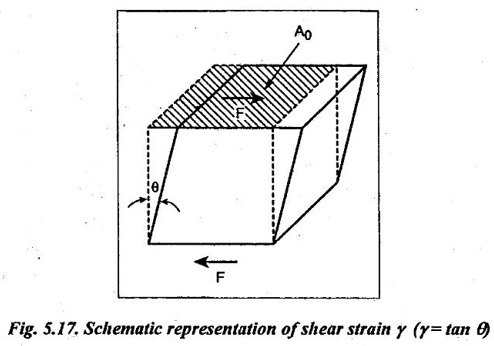
✔ Shear stress: The shear stress or shear strength is the value of load applied tangentially to shear it off across the resisting section. Mathematically,

Shear stress,τ = F / Ao ….. (5.13)

where

F = Shear force applied, and

Ao = Area of shear (as shown in Fig.5.17)

✔ Shear strain: The shear strain is defined as the tangent of the strain angle 0, as indicated in Fig.5.17.

Mathematically, shear strain, γ = tan θ

1. Testing Methods

✔ Three main systems used for shear tests are:

(i) Double shear system for round bar test-pieces using a fork and eye device;

(ii) Double knife shear system for specimens with a rectangular section; and

(iii) The shearing of a disc from sheet materials using a punch and die.

✓ The test equipment generally takes the form of attachments which can be used in conjunction with a universal testing machine.

✓ The disadvantages of these methods are:

■ Always there will be bending of the test-piece, therefore the stresses within the material will not be of the pure shear type, but they include bending stresses.

■ Very difficult to obtain accurate quantitative data from them.

2. Torsion Test

✓ Torsion is a variation of pure shear, wherein a structural member is twisted in the manner of Fig.5.18.

✓ Torsional forces produce a rotational motion about the longitudinal axis of one end of the member relative to the other end.

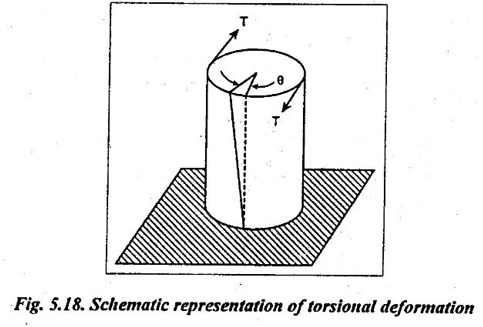
✓ To determine the shear strength t, the following general torsion equation can be applied within the elastic range :

where

τ = Shear stress

r = Radius of the cylinder,

T = Applied torque,

J = Second polar moment of area,

G = Modulus of rigidity of the material,

θ = Angle of twist in radians, and

L = Gauge length of the test-piece.