Hexagonal Close-Packed (HCP) Unit Cell

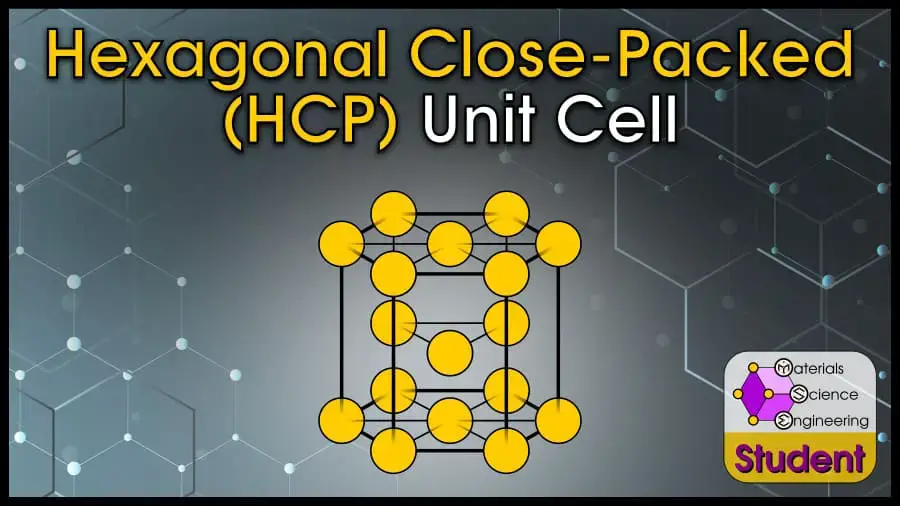
The Hexagonal Close-Packed (HCP) crystal structure is one of the most common ways for atoms to arrange themselves in metals. The HCP crystal structure is based on the Bravais lattice of the same name, with 1 atom per lattice point at each corner of the hexagonal prism, and 3 inside the prism. HCP is one of the most stable crystal structures and has the highest packing density. The hexagonal close-packed cell belongs to space group #194 or P63/mmc, Strukturbericht A3, and Pearson symbol hP2. Mg is the prototype for FCC.

The Hexagonal Close-Packed (HCP) unit cell can be imagined as a hexagonal prism with an atom on each vertex, and 3 atoms in the center. It can also be imagined as stacking 3 close-packed hexagonal layers such that the top layer and bottom layer line up. HCP is one of the most common structures for metals. HCP has 6 atoms per unit cell, lattice constant a = 2r and c = (4√6r)/3 (or c/a ratio = 1.633), coordination number CN = 12, and Atomic Packing Factor APF = 74%. HCP is a close-packed structure with AB-AB stacking.

Don’t worry, I’ll explain what those numbers mean and why they’re important later in the article. For now, let’s talk about which materials actually exist as face-centered cubic.

Outline

Common Examples of Hexagonal Close-Packed Materials

Since HCP is one of the most common crystal structures, there are many materials to choose from! Scandium, titanium, cobalt, zinc, yttrium, zirconium, technetium, ruthenium, cadmium, gadolinium, terbium, dysprosium, holmium, erbium, thulium, lutetium, hafnium, rhenium, osmium, and thallium all have an HCP structure at standard pressure and temperature. This list is not comprehensive; HCP can also be found in high temperature/pressure phases, or in alloys.

HCP is common because of its high coordination number.

Hexagonal Close-Packed Coordination Number

Coordination Number (CN) is the number of nearest neighbors that each atom has.

As a close-packed structure, the HCP crystal has the number of nearest-neighbors (NN): 12. Each of these NNs contributes a bond, giving the crystal structure very high stability.

Hexagonal Close-Packed Lattice Constants

The hexagonal close-packed lattice is a hexagonal prism with an atom on each vertex and three in center. Using the hard sphere model, which imagines each atom as a discrete sphere, the HCP crystal has each atom touch along the top and bottom of the prism.

You can also visualize the primitive HCP cell, which has an atom at each of 8 corners and another one near the center.

The HCP cell is defined by two lattice constants a and c, which correspond to two side lengths in the primitive cell (there is also a 3rd side length, b, but that’s the exact same as a).

$a$ is the distance between any two nearest atoms, which is also the length of each side of the hexagon.

Since $a$ is the distance between two touching atoms, a must be $2r$ .

Calculating $c$ is a bit trickier, but it can be done with trigonometry.

Click here to see the math!

If you look at the central atom in the primitive cell, you can see that it has a distance between the atoms in the plane above and in the plane below. If you projected the atom into one of those planes, it would be exactly in the middle of 3 atoms.

This position is the center of the equilateral triangle.

Let’s draw a line between the center of the triangle and one of its corners. We can call this $d$ . Because the angles of an equilateral triangle are all 60°, the angle between $d$ and $\frac{a}{2}$ is 30°.

$\cos\left(30^{\circ} \right)=\frac{\left(\frac{a}{2}\right)}{d}$

$d=\frac{a}{\sqrt{3}}$

Now we can make another triangle, between $d$ , $\frac{c}{2}$ , and $a$ .

$\left(d\right)^2+\left(\frac{c}{2}\right)^2=a^2$

$\left(\frac{a}{\sqrt{3}}\right)^2+\left(\frac{c}{2}\right)^2=a^2$

Which means that

$c=\sqrt{\frac{8}{3}}a$

$\frac{c}{a}\approx 1.633$

And remembering that $a=2r$ ,

$c=4\sqrt{\frac{2}{3}}$

Now we can make another triangle, between $d$ , $\frac{c}{2}$ , and $a$ .

$\left(d\right)^2+\left(\frac{c}{2}\right)^2=a^2$

$\left(\frac{a}{\sqrt{3}}\right)^2+\left(\frac{c}{2}\right)^2=a^2$

Which means that

$c=\sqrt{\frac{8}{3}}a$

$\frac{c}{a}\approx 1.633$

And remembering that $a=2r$ ,

$c=4\sqrt{\frac{2}{3}}$

If you go through the math, you’ll find that c should be about 1.6a in a perfect HCP crystal.

If you wanted to describe the hexagonal close-packed crystal with math, you would describe the cell with the vectors:

$\vec{a}_1=\frac{a}{2}\hat{x}-\frac{\sqrt{3}a}{2}\hat{y}$
$\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}$
$\vec{a}_3=c\hat{z}$

These are actually primitive vectors, which you can read about in the section below.

Hexagonal Close-Packed Atomic Packing Factor

The Atomic Packing Factor (APF) is essentially the density of the unit cell. Since we use the hard sphere model, each point inside the cell is either part of an atom, or part of the void.

APF is basically the fraction of atoms to void. For a full article explaining APF, check out this link.

APF is the

$APF=\frac{volume\:taken\:by\:atoms}{total\:volume}$

The total volume of the unit cell is the area of one hexagon, multiplied by the height of the prism.

Click here to see the math!

Start by breaking this into parts. The volume of the hexagonal prism will be the area of the hexagon * the height of the prism. The area of the hexagon is just 6 equilateral triangles.

Let’s start by calculating the area of a single triangle. Any triangle’s area is

$Area_{Triangle}=\frac{1}{2}Base\cdot Height$

Each side of the triangle has a length $a$ , so let’s use that as our base. Now we need to find the height of the triangle.

Once again, the pythagorean theorem saves the day! We can make right triangle between $\frac{a}{2}$ , $a$ , and the height $h$ .

$\left(\frac{a}{2}\right)^2+h^2=a^2$

Which means

$h=\sqrt{a^2-\left(\frac{a}{2}\right)^2}$

So the area of the triangle is

$Area_{Triangle}=\frac{a}{2}\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\sqrt{\frac{3}{4}}a^2$

And since there are 6 equilateral triangles per hexagon,

$Area_{Hexagon}=6Area_{Triangle}=\frac{3\sqrt{3}}{2}$

Multiplying this area by the height gives

$Volume_{HCP\:cell}=\frac{3\sqrt{3}}{2}a^2c$

and using $c=\sqrt{\frac{8}{3}}a$ and $a=2r$ ,

$Volume_{HCP\:cell}=24\sqrt{2}r^3$

Now we need to count how many atoms are in each unit cell. It may look like there are 17 atoms in the HCP unit cell, but that’s actually the number of different atoms that intersect the unit cell. Most of those atoms are only partially inside the cell.

If you count the portion of atoms in the cell, ⅙ of each vertex atom would count. Since there are 12 vertex atoms, $12\cdot\frac{1}{6}=2$ . There is also a half atom on the top and bottom faces, which adds to 1 more whole atom. Finally, there are 3 atoms fully inside the HCP unit cell.

Thus, there are 6 atoms per unit cell.

If we write everything in terms of the radius of an atom, you can see that every face-centered cubic crystal will have the same packing factor regardless of the actual element.

The volume of a sphere is $\frac{4}{3}\pi r^3$ . We previously established that the area of the whole cell is $24\sqrt{2}r^3$ , so the APF of HCP is

$APF_{HCP}=\frac{\left(\frac{12}{6}+\frac{2}{2}+\frac{3}{1}\right)\frac{4}{3}\pi \:r^3}{24\sqrt{2}r^3}=\frac{\pi \:}{3\sqrt{2}}\approx \:74\%$

As you can see, hexagonal close-packed crystals have 74% packing. That is exactly the same value as face-centered cubic (FCC) crystals, because both HCP and FCC are close-packed structures with the maximum possible APF (although it is possible to have higher packing if you use multiple kinds of atoms with different sizes).

In addition to FCC and HCP, it is possible to have other close-packed structures such as the close-packed rhombohedral structure found in samarium. It all comes down to stacking order.

Primitive Hexagonal Close-Packed Unit Cell

Advanced topic, click to expand!

I already mentioned this before, but both the conventional and primitive HCP cells are commonly used. The conventional cell has advantages because it is highly symmetric and easy for humans to understand. The primitive cell is smaller which can make mathematical manipulation easier.

When dealing with mathematical descriptions of crystals, it’s often easier to describe the unit cell in the smallest form possible (that’s the definition of a primitive cell). If you are interested in primitive cells, you can read all about them in this article.

You’ve already seen the HCP primitive cell, but in case you were skipping to this section:

Here are the primitive vectors for the HCP unit cell

$\vec{a}_1=\frac{a}{2}\hat{x}-\frac{\sqrt{3}a}{2}\hat{y}$
$\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}$
$\vec{a}_3=c\hat{z}$

Interstitial Sites in Hexagonal Close-Packed

Interstitial sites are the spaces inside a crystal where another kind of atom could fit. HCP has two types of interstitial sites: octahedral and tetrahedral. (Technically trigonal sites are also possible, but they are not practically useful).

HCP has 6 octahedral sites, which means that a small interstitial atom could fit in 6 positions such that it is equally surrounded by 6 HCP lattice atoms.

These octahedral interstitial sites have a radius of 0.414R, where r is the radius of the lattice atoms.

HCP also has 12 tetrahedral sites, which means that a small interstitial atom could fit in 12 positions such that it is equally surrounded by 4 HCP lattice atoms.

These tetrahedral atoms can be 0.225R, where r is the radius of the lattice atoms.

Slip Systems in Hexagonal Close-Packed

Advanced topic, click to expand!

Slip systems are the way that atoms slide past each other when deforming. Slip systems determine many mechanical properties of materials, and is the main reason why a material will be ductile or brittle.

To understand slip system directions, you will need to be familiar with Miller Indices notation, (we’re preparing an article about it). I’ll be using the notation for a primitive cell (3 numbers) instead of the conventional HCP cell (4 numbers).

The HCP close-packed planes are {001}, so those are the slip planes. Within the {001} planes, the slip direction (close-packed direction) is <100>. You can see in this (001) plane, there are 3 slip directions: [100], [110], and [010].

However, since [110] can be made by the linear combination of [100] and [010], there are actually only 2 independent slip systems.

These are called the basal slip systems in HCP.

\hkl<11\overline{2}0> — Slip Systems in HCP

There are also prismatic and pyramidal slip systems in HCP. These systems, however, are not necessarily close-packed, and may need to be thermally activated.

Because not all HCP metals have all at least 5 independent slip systems active at room temperature, not all HCP metals are ductile at room temperature. In some metals, the atoms don’t have the ideal c/a ratio, which deactivates slip systems. In other metals, the slip systems can be thermally activated to provide ductility. For example, titanium is ductile at room temperature, but zinc will only become ductile after it’s heated.

Final Thoughts

The Hexagonal Close-Packed (HCP) crystal structure is one of the most common ways that atoms can be arranged in pure solids. HCPis close-packed, which means it has the maximum APF of 0.74. Because HCP structures are often imperfect (specifically, they don’t have the c/a ratio we calculated), they may not have enough slip systems active to allow ductility. That’s why HCP metals can have dramatically different properties.

Here is a summary chart of all HCP crystal properties:

Crystal Structure	Hexagonal Close-Packed
Unit Cell Type	Hexagonal
Relationship Between Cube Edge Length a and the Atomic Radius R	a = 2R
Close-Packed Structure	Yes
Atomic Packing Factor (APF)	74%
Coordination Number	12
Number of Atoms per Unit Cell	6
Number of Octahedral Interstitial Sites	6
Number of Tetrahedral Interstitial Sites	12
Size of Octahedral Voids	r = 0.414R
Size of Tetrahedral Voids	r = 0.225R

Name of a Slip System	Number of Slip Systems	Slip Plane	Slip Direction
Basal	3	$\left\{0001\right\}$	$\hkl<11\overline{2}0>$
Prismatic	3	$\left\{00\overline{1}0\right\}$	$\hkl<11\overline{2}0>$
Pyramidal	12	$\left\{00\overline{1}1\right\}$	$\hkl<11\overline{23}>$

VEERAPANDIAN.K , Assistant Professor

Pages

Friday, November 17, 2023